Индекс сложности

В современной информатике и статистике индекс сложности функции обозначает уровень информативности, что, в свою очередь, влияет на сложность изучения функции на примерах . Это отличается от вычислительной сложности , которая представляет собой сложность вычисления функции. Индексы сложности характеризуют весь класс функций, к которому принадлежит интересующая нас функция. Сосредоточив внимание на логических функциях , детали класса ${\mathsf {C}}$ булевых функций c по сути означает, насколько глубоко сформулирован класс.

Техническое определение

Чтобы идентифицировать этот индекс, мы должны сначала определить сторожевую функцию ${\mathsf {C}}$ .Давайте на мгновение сосредоточимся на одной функции c , назовем ее концепцией, определенной на множестве ${\mathcal {X}}$ элементов, которые мы можем представить как точки в евклидовом пространстве . В этой структуре вышеуказанная функция связывает с c набор точек, которые, поскольку определены как внешние по отношению к понятию, не позволяют ему расшириться в другую функцию ${\mathsf {C}}$ . Мы можем двояко определить эти точки с точки зрения защиты данного понятия c от полного включения (вторжения) в другое понятие внутри класса. Поэтому мы называем эти точки либо дозорными , либо сторожевыми точками ; они назначаются сторожевой функцией ${\boldsymbol {S}}$ к каждому понятию ${\mathsf {C}}$ таким образом, что:

сторожевые точки являются внешними по отношению к понятию c, которое должно быть сигнализировано, и внутренними по крайней мере для одного другого, включая его,
каждая концепция $c'$ включая c, имеет хотя бы одну из сторожевых точек c либо в промежутке между c и $c'$ или снаружи $c'$ и отличается от сторожевых пунктов $c'$ , и
они составляют минимальный набор с этими свойствами.

Техническое определение, взятое из ( Apoloni 2006 ), основано на включении расширенной концепции. $c^{+}$ состоит из c плюс его сторожевые точки, созданные другим $\left(c'\right)^{+}$ в том же классе.

Определение сторожевой функции

Для концептуального класса ${\mathsf {C}}$ на пространстве ${\mathfrak {X}}$ , сторожевая функция — это полная функция ${\boldsymbol {S}}:{\mathsf {C}}\cup \{\emptyset ,{\mathfrak {X}}\}\mapsto 2^{\mathfrak {X}}$ удовлетворяющий следующим условиям:

Стражи находятся за пределами концепции дозорных ( $c\cap {\boldsymbol {S}}(c)=\emptyset$ для всех $c\in {\mathsf {C}}$ ) .
Стражи находятся внутри концепции вторжения ( Введя наборы $c^{+}=c\cup {\boldsymbol {S}}(c)$ , вторгающаяся концепция $c'\in {\mathsf {C}}$ таков, что $c'\not \subseteq c$ и $c^{+}\subseteq \left(c'\right)^{+}$ . Обозначая $\mathrm {up} (c)$ набор понятий, вторгающихся в c , мы должны иметь это, если $c_{2}\in \mathrm {up} (c_{1})$ , затем $c_{2}\cap {\boldsymbol {S}}(c_{1})\neq \emptyset$ ) .
${\boldsymbol {S}}(c)$ — минимальное множество с указанными выше свойствами ( Нет ${\boldsymbol {S}}'\neq {\boldsymbol {S}}$ существует, удовлетворяя (1) и (2) и обладая тем свойством, что ${\boldsymbol {S}}'(c)\subseteq {\boldsymbol {S}}(c)$ для каждого $c\in {\mathsf {C}}$ ) .
Стражи – честные стражи. Может быть, это $c\subseteq \left(c'\right)^{+}$ но ${\boldsymbol {S}}(c)\cap c'=\emptyset$ так что $c'\not \in \mathrm {up} (c)$ . Однако это должно быть следствием того факта, что все пункты ${\boldsymbol {S}}(c)$ участвуют в реальном сопоставлении c с другими концепциями в $\mathrm {up} (c)$ и не только в том, чтобы избежать включения $c^{+}$ к $(c')^{+}$ . Таким образом, если мы удалим $c',{\boldsymbol {S}}(c)$ остается неизменным ( всякий раз, когда $c_{1}$ и $c_{2}$ таковы, что $c_{1}\subset c_{2}\cup {\boldsymbol {S}}(c_{2})$ и $c_{2}\cap {\boldsymbol {S}}(c_{1})=\emptyset$ , то ограничение ${\boldsymbol {S}}$ к $\{c_{1}\}\cup \mathrm {up} (c_{1})-\{c_{2}\}$ является сторожевой функцией на этом множестве ) .

${\boldsymbol {S}}(c)$ это граница c на ${\boldsymbol {S}}$ .

Схематическое представление о функциональности внешнего дозорного

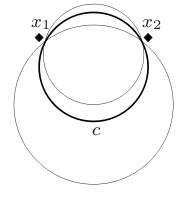
Что касается изображения справа, $\{x_{1},x_{2},x_{3}\}$ является кандидатской границей $c_{0}$ против $c_{1},c_{2},c_{3},c_{4}$ . Все точки находятся в промежутке между $c_{i}$ и $c_{0}$ . Они избегают включения $c_{0}\cup \{x_{1},x_{2},x_{3}\}$ в $c_{3}$ , при условии, что эти точки не используются последним для защиты от других концепций. И наоборот, мы ожидаем, что $c_{1}$ использует $x_{1}$ и $x_{3}$ как свои собственные стражи, $c_{2}$ использует $x_{2}$ и $x_{3}$ и $c_{4}$ использует $x_{1}$ и $x_{2}$ аналогично. Точка $x_{4}$ не допускается как $c_{0}$ сторожевой пункт, поскольку, как и любое дипломатическое место, он должен располагаться вне всех других концепций, просто чтобы гарантировать, что он не будет занят в случае вторжения $c_{0}$ .

Определение деталей

Граничный размер самой дорогой концепции, которая будет отслеживаться с помощью наименее эффективной контрольной функции, т. е. количества

\mathrm {D} _{\mathsf {C}}=\sup _{{\boldsymbol {S}},c}\#{\boldsymbol {S}}(c)

,

называется деталью ${\mathsf {C}}$ . ${\boldsymbol {S}}$ охватывает также сторожевые функции на подмножествах ${\mathfrak {X}}$ отслеживая в этом случае пересечения понятий с этими подмножествами. На самом деле, правильные подмножества ${\mathfrak {X}}$ могут выполнять задачи по дозору, которые оказываются сложнее, чем те, которые возникают с ${\mathfrak {X}}$ сам.

Деталь $\mathrm {D} _{\mathsf {C}}$ является мерой сложности классов концептов, двойственных измерению VC. $\mathrm {D} _{{\mathsf {V}}C}$ . Первый использует точки для разделения наборов понятий, второй — для разделения наборов точек. В частности, имеет место следующее неравенство ( Аполлони 1997 ):

\mathrm {D} _{\mathsf {C}}\leq \mathrm {D} _{{\mathsf {V}}C}+1

См. также сложность Радемахера , чтобы узнать о недавно введенном индексе сложности класса.

Пример: непрерывные пространства

Класс C кругов в $\mathbb {R} ^{2}$ есть детали $\mathrm {D} _{\mathsf {C}}=2$ , как показано на рисунке слева внизу. Аналогично для класса отрезков на $\mathbb {R}$ , как показано на рисунке справа.

Две точки $x_{1},x_{2}$ за пределами c (толстый круг) достаточно, чтобы предотвратить включение его в больший круг, не содержащий их.

Класс сегментов в

\mathbb {R}

и два пункта, необходимые для отражения его концепций

Пример: дискретные пространства

Класс ${\mathsf {C}}=\{c_{1},c_{2},c_{3},c_{4}\}$ на ${\mathfrak {X}}=\{x_{1},x_{2},x_{3}\}$ понятия которого проиллюстрированы на следующей схеме, где «+» обозначает элемент $x_{j}$ принадлежащий $c_{i}$ , "-" элемент снаружи $c_{i}$ , и ⃝ сторожевой пункт:

	$x_{1}$	$x_{2}$	$x_{3}$
$c_{1}=$	-⃝	-⃝	-
$c_{2}=$	-⃝	+	+
$c_{3}=$	+	-⃝	+
$c_{4}=$	+	+	+

Этот класс имеет $\mathrm {D} _{\mathsf {C}}=2$ . Как обычно, у нас могут быть разные функции дозора. Наихудший случай $S$ , как показано, таков: $\mathbf {S} (c_{1})=\{x_{1},x_{2}\},\mathbf {S} (c_{2})=\{x_{1}\},\mathbf {S} (c_{3})=\{x_{2}\},\mathbf {S} (c_{4})=\emptyset$ . Однако более дешевый вариант $\mathbf {S} (c_{1})=\{x_{3}\},\mathbf {S} (c_{2})=\{x_{1}\},\mathbf {S} (c_{3})=\{x_{2}\},\mathbf {S} (c_{4})=\emptyset$ :

	$x_{1}$	$x_{2}$	$x_{3}$
$c_{1}=$	-	-	-⃝
$c_{2}=$	-⃝	+	+
$c_{3}=$	+	-⃝	+
$c_{4}=$	+	+	+

Ссылки

Аполлони, Б.; Мальчиоди, Д.; Гайто, С. (2006). Алгоритмический вывод в машинном обучении . Международная серия по передовому интеллекту. Том. 5 (2-е изд.). Аделаида: Мэгилл. Передовые знания Международные
Аполлони, Б.; Кьяравалли, С. (1997). «PAC-обучение концептуальных классов через границы их предметов» . Теоретическая информатика . 172 (1–2): 91–120. дои : 10.1016/S0304-3975(95)00240-5 .