Числовой диапазон продукта

Учитывая гильбертово пространство с произведения, тензорной структурой числовой диапазон произведения определяется как числовой диапазон относительно подмножества векторов произведения. В некоторых ситуациях, особенно в контексте квантовой механики, числовой диапазон произведения известен как локальный числовой диапазон.

Введение

Позволять $X$ быть оператором, действующим на $N$-мерное гильбертово пространство ${\mathcal {H}}_{N}$. Позволять $\mathrm {\Lambda } (X)$ обозначают его числовой диапазон , т.е. совокупность всех $\lambda$ такое, что существует нормализованное состояние ${|\psi \rangle }\in {\mathcal {H}}_{N}$, $||\psi ||=1$, что удовлетворяет ${\langle \psi |}X{|\psi \rangle }=\lambda$.

Аналогичное понятие можно определить для операторов, действующих в составном гильбертовом пространстве со структурой тензорного произведения. Рассмотрим сначала двудольное гильбертово пространство: ${\mathcal {H}}_{N}={\mathcal {H}}_{K}\otimes {\mathcal {H}}_{M},$ составного размера $N=KM$.

Позволять $X$ — оператор, действующий в составном гильбертовом пространстве. Определяем числовой диапазон продукта $\mathrm {\Lambda } ^{\!\otimes }\!\left(X\right)$ из $X$относительно тензорной структуры произведения ${\mathcal {H}}_{N}$, как $\mathrm {\Lambda } ^{\!\otimes }\!\left(X\right)=\left\{{\langle \psi _{A}\otimes \psi _{B}|}X{|\psi _{A}\otimes \psi _{B}\rangle }:{|\psi _{A}\rangle }\in {\mathcal {H}}_{K},{|\psi _{B}\rangle }\in {\mathcal {H}}_{M}\right\},$ где ${|\psi _{A}\rangle }\in {\mathcal {H}}_{K}$ и ${|\psi _{B}\rangle }\in {\mathcal {H}}_{M}$ нормируются.

Числовой радиус продукта

Позволять ${\mathcal {H}}_{N}={\mathcal {H}}_{K}\otimes {\mathcal {H}}_{M}$ быть тензорным произведением гильбертова пространства. Определим числовой радиус изделия $r^{\otimes }(X)$ из $X$, относительно этой структуры тензорного произведения, как $r^{\otimes }(X)=\max\{|z|:z\in \mathrm {\Lambda } ^{\!\otimes }\!\left(X\right)\}.$

Обозначения

Понятие числового диапазона данного оператора, также называемое «полем значений», широко изучалось в течение последних нескольких десятилетий, и была подчеркнута его полезность в квантовой теории. Известны несколько обобщений числового диапазона. В частности, Маркус ввел понятие «разложимого числового диапазона», свойства которого представляют собой предмет значительного интереса.

Числовой диапазон произведения можно рассматривать как частный случай разложимого числового диапазона, определенного для операторов, действующих в гильбертовом пространстве тензорного произведения. Это понятие также можно рассматривать как числовой диапазон относительно соответствующей подгруппы. $U(K)\times U(M)$ полной унитарной группы $U(KM)$.

Общий случай

Нетрудно установить основные свойства числового диапазона произведения, не зависящие от разбиения гильбертова пространства и структуры оператора. Мы перечислим их ниже, оставив некоторые простые пункты без доказательств.

Основные свойства

Топологические факты, касающиеся числового диапазона произведений для общих операторов.

1. Числовой ряд произведений образует связное множество на комплексной плоскости. Это верно, поскольку числовой диапазон продукта представляет собой непрерывный образ связанного множества.
2. Числовой диапазон продукта является субаддитивным. Для всех $A,B\in \mathbb {M} _{n}$ $\mathrm {\Lambda } ^{\!\otimes }\!\left(A+B\right)\subset \mathrm {\Lambda } ^{\!\otimes }\!\left(A\right)+\mathrm {\Lambda } ^{\!\otimes }\!\left(B\right).$
3. Для всех $A\in \mathbb {M} _{n}$ и $\alpha \in \mathbb {C}$ $\mathrm {\Lambda } ^{\!\otimes }\!\left({A+\alpha \mathbf {I} }\right)=\mathrm {\Lambda } ^{\!\otimes }\!\left(A\right)+\alpha .$
4. Для всех $A\in \mathbb {M} _{n}$ и $\alpha \in \mathbb {C}$ $\mathrm {\Lambda } ^{\!\otimes }\!\left({\alpha A}\right)=\alpha \mathrm {\Lambda } ^{\!\otimes }\!\left({A}\right).$
5. Для всех $A\in \mathbb {M} _{m\times n}$ $\mathrm {\Lambda } ^{\!\otimes }\!\left({(U\otimes V)A(U\otimes V)^{\dagger }}\right)=\mathrm {\Lambda } ^{\!\otimes }\!\left({A}\right),$ для унитарного $U\in \mathbb {M} _{m}$ и $V\in \mathbb {M} _{n}$.
6. Позволять $A\in \mathbb {M} _{m}$ и $B\in \mathbb {M} _{n}$

• Если один из них нормальный, то числовой диапазон их тензорного произведения совпадает с выпуклой оболочкой числового диапазона произведения: $\mathrm {\Lambda } (A\otimes B)=\mathrm {Co} (\mathrm {\Lambda } ^{\!\otimes }\!\left({A\otimes B}\right)).$
• Если $e^{i\theta }A$ является положительно полуопределенным для некоторых $\theta \in [0,2\pi )$, затем $\mathrm {\Lambda } (A\otimes B)=\mathrm {\Lambda } ^{\!\otimes }\!\left({A\otimes B}\right).$
• Позволять $H(A)={\frac {1}{2}}(A+A^{\dagger })$ и $S(A)={\frac {1}{2}}(A-A^{\dagger })$.

1. Для всех $A\in \mathbb {M} _{n}$, у нас есть $\mathrm {\Lambda } ^{\!\otimes }\!\left({H(A)}\right)=\mathrm {Re} \ \mathrm {\Lambda } ^{\!\otimes }\!\left({A}\right)$ и $\mathrm {\Lambda } ^{\!\otimes }\!\left({S(A)}\right)=i\,\mathrm {Im} \ \mathrm {\Lambda } ^{\!\otimes }\!\left({A}\right).$

Выпуклость

Числовой диапазон продукта не обязательно должен быть выпуклым. Рассмотрим следующий простой пример. Позволять

$A=\left({\begin{array}{cc}1&0\\0&0\end{array}}\right)\otimes \left({\begin{array}{cc}1&0\\0&0\end{array}}\right)+i\left({\begin{array}{cc}0&0\\0&1\end{array}}\right)\otimes \left({\begin{array}{cc}0&0\\0&1\end{array}}\right).$

Матрица $A$ определенное выше является матрицей с собственными значениями $0,1,i$. Это легко увидеть $1\in \mathrm {\Lambda } ^{\!\otimes }\!\left({A}\right)$ и $i\in \mathrm {\Lambda } ^{\!\otimes }\!\left({A}\right)$, но $(1+i)/2\not \in \mathrm {\Lambda } ^{\!\otimes }\!\left({A}\right)$. Действительно, прямым вычислением имеем $\mathrm {\Lambda } ^{\!\otimes }\!\left({A}\right)=\left\{x+yi:0\leq x,0\leq y,{\sqrt {x}}+{\sqrt {y}}\leq 1\right\}.$

Числовой диапазон продукта матрицы $A$ представлено ниже.

Сравнение числового диапазона (серый треугольник) и числового диапазона продукта (пунктир) для матрицы A.

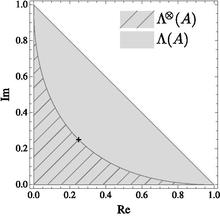
Числовой диапазон произведений образует непустое множество для общего оператора. В частности, он содержит барицентр спектра.

Барицентр

Числовой диапазон продукта $A\in \mathbb {M} _{K\times M}$ включает барицентр спектра, ${\frac {1}{KM}}\;{\mathrm {tr} }A\ \in \ \mathrm {\Lambda } ^{\!\otimes }\!\left({A}\right).$

Числовой радиус произведения является векторной нормой матриц, но не матричной нормой. Числовой радиус произведения инвариантен относительно локальных унитарных единиц, которые имеют структуру тензорного произведения.

Ссылки

• З. Пухала, П. Гаврон, Я. А. Мищак, Л. Сковронек, М.-. Чой, К. Зискковски, «Числовой диапазон произведения в пространстве с тензорной структурой произведения», Linear Algebra Appl., 434 (2011) 327–342. doi : 10.1016/j.laa.2010.08.026 arXiv : 1008.3482 .
• П. Гаврон, З. Пухала, Я. А. Мищак, Л. Сковронек, К. Зискковски, «Ограниченный числовой диапазон: универсальный инструмент в теории квантовой информации», J. Math. Физ. 51, 102204 (2010). doi : 10.1063/1.3496901 arXiv : 0905.3646 .