Путь Дубина

В геометрии термин «путь Дубинса» обычно относится к кратчайшей кривой, которая соединяет две точки в двумерной евклидовой плоскости (т. е. плоскости xy ) с ограничением на кривизну пути и с заданными начальными и конечными касательными к пути, и предположение, что транспортное средство, движущееся по пути, может двигаться только вперед. Если транспортное средство также может двигаться задним ходом, то путь следует кривой Ридса – Шеппа. ^[1]

Лестер Эли Дубинс (1920–2010) ^[2] доказано с помощью инструментов анализа ^[3] что любой такой путь будет состоять из сегментов максимальной кривизны и/или прямых линий. Другими словами, кратчайший путь будет получен путем соединения дуг окружностей максимальной кривизны и прямых линий.

Обсуждение

Дубинс доказал свой результат в 1957 году. В 1974 году Гарольд Х. Джонсон доказал результат Дубинса, применив принцип максимума Понтрягина . ^[4] В частности, Гарольд Х. Джонсон представил необходимые и достаточные условия для того, чтобы плоская кривая, имеющая ограниченную кусочно-непрерывную кривизну и заданные начальные и конечные точки и направления, имела минимальную длину. В 1992 году тот же результат был снова показан с использованием принципа максимума Понтрягина . ^[5] Совсем недавно доказательство на основе геометрической теории кривых было предоставлено Дж. Айялой, Д. Кирсенблатом и Дж. Хайамом Рубинштейном. ^[6] Доказательство, характеризующее пути Дубинса в гомотопических классах, было дано Дж. Айялой. ^[7]

Приложения

Путь Дубинса обычно используется в области робототехники и теории управления как способ планирования траекторий колесных роботов, самолетов и подводных аппаратов. Есть простые геометрические ^[8] и аналитические методы ^[9] рассчитать оптимальный путь.

Например, в случае с колесным роботом простая кинематическая модель автомобиля (также известная как машина Дубинса) для систем выглядит следующим образом: ${\begin{aligned}{\dot {x}}&=V\cos(\theta )\\{\dot {y}}&=V\sin(\theta )\\{\dot {\theta }}&=u\end{aligned}}$ где $(x,y)$ это положение автомобиля, $\theta$ это курс, машина движется с постоянной скоростью $V$ и регулятор скорости поворота $u$ ограничен. В этом случае максимальная скорость поворота соответствует некоторому минимальному радиусу поворота (и, что эквивалентно, максимальной кривизне). Заданные начальная и конечная касательные соответствуют начальному и конечному направлениям . Путь Дубинса дает кратчайший путь, соединяющий две ориентированные точки, который возможен для модели колесного робота.

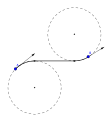
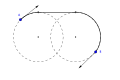
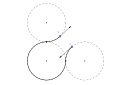
Оптимальный тип пути можно описать, используя аналогию с автомобилями, совершающими «поворот направо (R)», «поворот налево (L)» или движение «прямо (S)». Оптимальным путем всегда будет хотя бы один из шести типов: RSR, RSL, LSR, LSL, RLR, LRL. Например, предположим, что для некоторых заданных начального и конечного положений и касательных оптимальный путь имеет тип «RSR». Тогда это соответствует дуге поворота направо (R), за которой следует сегмент прямой (S), за которым следует еще одна дуга поворота направо (R). Перемещение по каждому сегменту этой последовательности на соответствующую длину сформирует кратчайшую кривую, которая соединяет начальную точку A с конечной точкой B с желаемыми касательными в каждой конечной точке и не превышает заданную кривизну.

Путь RSL Дубинса
Путь RSR Дубинса
Путь LRL Дубинса

Задача об интервале Дубинса

Проблема интервала Дубинса - это ключевой вариант задачи о пути Дубинса, где в начальной и конечной точках задан интервал направлений курса. Направление касательной к пути в начальной и конечной точках ограничено указанными интервалами. Эту проблему можно решить с помощью геометрического анализа. ^[10] или используя принцип минимума Понтрягина. ^[11]

Ссылки

^ Ридс, Дж.А.; Шепп, Луизиана (1990). «Оптимальные траектории для автомобиля, который движется как вперед, так и назад» . Тихоокеанский математический журнал . 145 (2): 367–393. дои : 10.2140/pjm.1990.145.367 .
^ «В ПАМЯТИ Лестера Эли Дубинса, профессор математики и статистики, почетный Калифорнийский университет в Беркли, 1920–2010» . Калифорнийский университет. Архивировано из оригинала 15 сентября 2011 года . Проверено 26 мая 2012 г.
^ Дубинс, Л.Е. (июль 1957 г.). «О кривых минимальной длины с ограничением на среднюю кривизну и с заданными начальными и конечными положениями и касательными». Американский журнал математики . 79 (3): 497–516. дои : 10.2307/2372560 . JSTOR 2372560 .
^ Джонсон, Гарольд Х. (1974). «Применение принципа максимума к геометрии плоских кривых» . Труды Американского математического общества . 44 (2): 432–435. дои : 10.1090/S0002-9939-1974-0348631-6 . МР 0348631 .
^ Буассона, Ж.-Д. ; Сересо, А.; Леблон, К. (май 1992 г.). «Кратчайшие пути ограниченной кривизны на плоскости» (PDF) . Материалы Международной конференции IEEE по робототехнике и автоматизации . Том. 3. Пискатауэй, Нью-Джерси. стр. 2315–2320. дои : 10.1109/РОБОТ.1992.220117 .
^ Айяла, Хосе; Кирзенблат, Дэвид; Рубинштейн, Хайам (2018). «Геометрический подход к кратчайшим путям ограниченной кривизны» . Коммуникации в анализе и геометрии . 26 (4): 679–697. arXiv : 1403.4899 . дои : 10.4310/CAG.2018.v26.n4.a1 .
^ Айяла, Хосе (2015). «Минимизирующие длину пути ограниченной кривизны в гомотопических классах» . Топология и ее приложения . 193 : 140–151. arXiv : 1403.4930 . дои : 10.1016/j.topol.2015.06.008 .
^ Аниси, Дэвид (июль 2003 г.). Оптимальное управление движением наземного транспортного средства (PDF) (Отчет). Шведское исследовательское оборонное агентство. 1650-1942.
^ Буй, Суан-Нам; Буассонна, Ж.-Д. ; Суэр, П.; Ломонд, Ж.-П. (май 1994 г.). «Синтез кратчайшего пути для неголономного робота Дубинса». Конференция IEEE по робототехнике и автоматизации . Том. 1. Сан-Диего, Калифорния. стр. 2–7. дои : 10.1109/РОБОТ.1994.351019 .
^ Маньям, Сатьянараяна; Ратинам, Сивакумар (2016). «О жестком ограничении оптимума коммивояжера Дубинса». Журнал динамических систем, измерений и управления . 140 (7): 071013. arXiv : 1506.08752 . дои : 10.1115/1.4039099 . S2CID 16191780 .
^ Маньям, Сатьянараяна Г.; Ратинам, Сивакумар; Касбир, Дэвид; Гарсия, Элой (2017). «Твердое ограничение кратчайших путей Дубинса через последовательность точек». Журнал интеллектуальных и робототехнических систем . 88 (2–4): 495–511. дои : 10.1007/s10846-016-0459-4 . S2CID 30943273 .

Внешние ссылки

Кривые Дубинса. Архивировано 22 марта 2016 г. в Wayback Machine , из книги Стивена М. ЛаВалле «Алгоритмы планирования».
Изохроны для автомобиля Дубинса , демонстрация из демонстрационного проекта Wolfram

[1] Ридс, Дж.А.; Шепп, Луизиана (1990). «Оптимальные траектории для автомобиля, который движется как вперед, так и назад» . Тихоокеанский математический журнал . 145 (2): 367–393. дои : 10.2140/pjm.1990.145.367 .

[2] «В ПАМЯТИ Лестера Эли Дубинса, профессор математики и статистики, почетный Калифорнийский университет в Беркли, 1920–2010» . Калифорнийский университет. Архивировано из оригинала 15 сентября 2011 года . Проверено 26 мая 2012 г.

[3] Дубинс, Л.Е. (июль 1957 г.). «О кривых минимальной длины с ограничением на среднюю кривизну и с заданными начальными и конечными положениями и касательными». Американский журнал математики . 79 (3): 497–516. дои : 10.2307/2372560 . JSTOR 2372560 .

[4] Джонсон, Гарольд Х. (1974). «Применение принципа максимума к геометрии плоских кривых» . Труды Американского математического общества . 44 (2): 432–435. дои : 10.1090/S0002-9939-1974-0348631-6 . МР 0348631 .

[5] Буассона, Ж.-Д. ; Сересо, А.; Леблон, К. (май 1992 г.). «Кратчайшие пути ограниченной кривизны на плоскости» (PDF) . Материалы Международной конференции IEEE по робототехнике и автоматизации . Том. 3. Пискатауэй, Нью-Джерси. стр. 2315–2320. дои : 10.1109/РОБОТ.1992.220117 .

[6] Айяла, Хосе; Кирзенблат, Дэвид; Рубинштейн, Хайам (2018). «Геометрический подход к кратчайшим путям ограниченной кривизны» . Коммуникации в анализе и геометрии . 26 (4): 679–697. arXiv : 1403.4899 . дои : 10.4310/CAG.2018.v26.n4.a1 .

[7] Айяла, Хосе (2015). «Минимизирующие длину пути ограниченной кривизны в гомотопических классах» . Топология и ее приложения . 193 : 140–151. arXiv : 1403.4930 . дои : 10.1016/j.topol.2015.06.008 .

[8] Аниси, Дэвид (июль 2003 г.). Оптимальное управление движением наземного транспортного средства (PDF) (Отчет). Шведское исследовательское оборонное агентство. 1650-1942.

[9] Буй, Суан-Нам; Буассонна, Ж.-Д. ; Суэр, П.; Ломонд, Ж.-П. (май 1994 г.). «Синтез кратчайшего пути для неголономного робота Дубинса». Конференция IEEE по робототехнике и автоматизации . Том. 1. Сан-Диего, Калифорния. стр. 2–7. дои : 10.1109/РОБОТ.1994.351019 .

[10] Маньям, Сатьянараяна; Ратинам, Сивакумар (2016). «О жестком ограничении оптимума коммивояжера Дубинса». Журнал динамических систем, измерений и управления . 140 (7): 071013. arXiv : 1506.08752 . дои : 10.1115/1.4039099 . S2CID 16191780 .

[11] Маньям, Сатьянараяна Г.; Ратинам, Сивакумар; Касбир, Дэвид; Гарсия, Элой (2017). «Твердое ограничение кратчайших путей Дубинса через последовательность точек». Журнал интеллектуальных и робототехнических систем . 88 (2–4): 495–511. дои : 10.1007/s10846-016-0459-4 . S2CID 30943273 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]