Чувствительность (системы управления)

В технике управления чувствительность передаточную (или, точнее, функция чувствительности ) системы управления измеряет, как изменения параметров объекта влияют на функцию с обратной связью . Поскольку параметры контроллера обычно соответствуют характеристикам процесса и процесс может меняться, важно, чтобы параметры контроллера выбирались таким образом, чтобы система с замкнутым контуром не была чувствительна к изменениям динамики процесса. Более того, функция чувствительности также важна для анализа того, как возмущения влияют на систему.

Функция чувствительности

Базовая система управления с замкнутым контуром, использующая единичную отрицательную обратную связь. C(s) и G(s) обозначают передаточные функции компенсатора и объекта соответственно.

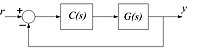
Позволять $G(s)$ и $C(s)$ обозначают передаточную функцию объекта и контроллера в базовой системе управления с замкнутым контуром, написанной в области Лапласа с использованием единичной отрицательной обратной связи .

Функция чувствительности как мера устойчивости к изменению параметров

Передаточная функция с обратной связью определяется выражением

$T(s)={\frac {G(s)C(s)}{1+G(s)C(s)}}.$

Дифференциация $T$ относительно $G$ урожайность

${\frac {dT}{dG}}={\frac {d}{dG}}\left[{\frac {GC}{1+GC}}\right]={\frac {C}{(1+CG)^{2}}}=S{\frac {T}{G}},$

где $S$ определяется как функция

$S(s)={\frac {1}{1+G(s)C(s)}}$

и известна как функция чувствительности . Более низкие значения $|S|$ подразумевает, что относительные ошибки в параметрах объекта меньше влияют на относительную ошибку передаточной функции замкнутого контура.

Функция чувствительности как мера затухания помех

Функция чувствительности также описывает передаточную функцию от внешнего возмущения к выходному сигналу процесса. Фактически, предполагая аддитивное возмущение n после выхода

объекта передаточные функции замкнутой системы имеют вид

$Y(s)={\frac {C(s)G(s)}{1+C(s)G(s)}}R(s)+{\frac {1}{1+C(s)G(s)}}N(s).$

Следовательно, более низкие значения $|S|$ предполагают дальнейшее ослабление внешнего возмущения. Функция чувствительности говорит нам, как на возмущения влияет обратная связь. Возмущения с такими частотами, что $|S(j\omega )|$ меньше единицы, уменьшаются на величину, равную расстоянию до критической точки $-1$ и возмущения с такими частотами, что $|S(j\omega )|$ больше единицы, усиливаются обратной связью. ^[1]

Пик чувствительности и круг чувствительности

Пик чувствительности

Важно, чтобы для системы управления было ограничено наибольшее значение функции чувствительности. Номинальный пик чувствительности $M_{s}$ определяется как ^[2]

$M_{s}=\max _{0\leq \omega <\infty }\left|S(j\omega )\right|=\max _{0\leq \omega <\infty }\left|{\frac {1}{1+G(j\omega )C(j\omega )}}\right|$

и обычно требуется, чтобы максимальное значение функции чувствительности $M_{s}$ находиться в диапазоне от 1,3 до 2.

Круг чувствительности

Количество $M_{s}$ является обратной величиной кратчайшего расстояния от кривой Найквиста петлевой передаточной функции до критической точки. $-1$ . Чувствительность $M_{s}$ гарантирует, что расстояние от критической точки до кривой Найквиста всегда больше, чем ${\frac {1}{M_{s}}}$ а кривая Найквиста петлевой передаточной функции всегда находится вне круга вокруг критической точки. $-1+0j$ с радиусом ${\frac {1}{M_{s}}}$ , известный как круг чувствительности . $M_{s}$ определяет максимальное значение функции чувствительности и обратную величину $M_{s}$ дает вам кратчайшее расстояние от передаточной функции разомкнутого контура $L(j\omega )$ до критической точки $-1+0j$ . ^[3]^[4]

Ссылки

^ К. Дж. Астром, «Неопределенность модели и надежный контроль», в конспектах лекций по итеративной идентификации и проектированию управления. Лунд, Швеция: Лундский технологический институт, январь 2000 г., стр. 63–100.
^ К. Дж. Астром и Т. Хагглунд, ПИД-регуляторы: теория, проектирование и настройка, 2-е изд. Research Triangle Park, Северная Каролина 27709, США: ISA - Общество приборов, систем и автоматизации, 1995.
^ А. Г. Йепес и др., «Анализ и проектирование регуляторов резонансного тока для преобразователей напряжения с помощью диаграмм Найквиста и функции чувствительности» в IEEE Trans. по промышленной электронике, вып. 58, № 11, ноябрь 2011 г., стр. 5231–5250.
^ Карл Йохан Острем и Ричард М. Мюррей. Системы обратной связи: введение для ученых и инженеров. Издательство Принстонского университета, Принстон, Нью-Джерси, 2008.

См. также

[1] К. Дж. Астром, «Неопределенность модели и надежный контроль», в конспектах лекций по итеративной идентификации и проектированию управления. Лунд, Швеция: Лундский технологический институт, январь 2000 г., стр. 63–100.

[2] К. Дж. Астром и Т. Хагглунд, ПИД-регуляторы: теория, проектирование и настройка, 2-е изд. Research Triangle Park, Северная Каролина 27709, США: ISA - Общество приборов, систем и автоматизации, 1995.

[3] А. Г. Йепес и др., «Анализ и проектирование регуляторов резонансного тока для преобразователей напряжения с помощью диаграмм Найквиста и функции чувствительности» в IEEE Trans. по промышленной электронике, вып. 58, № 11, ноябрь 2011 г., стр. 5231–5250.

[4] Карл Йохан Острем и Ричард М. Мюррей. Системы обратной связи: введение для ученых и инженеров. Издательство Принстонского университета, Принстон, Нью-Джерси, 2008.

[1]

[2]

[3]

[4]