Алгоритм альфа-макс плюс бета-мин

Не путать с минимаксной или альфа-бета-обрезкой .

Геометрическое положение точек, дающих одно и то же значение в алгоритме, для разных значений альфа и бета.

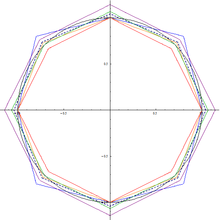
Алгоритм альфа-макс плюс бета-мин. представляет собой высокоскоростную аппроксимацию квадратного корня из суммы двух квадратов. Квадратный корень из суммы двух квадратов, также известный как сложение Пифагора , является полезной функцией, поскольку он находит гипотенузу прямоугольного треугольника по двум длинам сторон, норме двумерного вектора или величине. $|z|={\sqrt {a^{2}+b^{2}}}$ комплексного числа z = a + bi с учетом действительной и мнимой частей.

Алгоритм избегает выполнения операций возведения в квадрат и извлечения квадратного корня, вместо этого используются простые операции, такие как сравнение, умножение и сложение. Некоторый выбор параметров алгоритма α и β позволяет свести операцию умножения к простому сдвигу двоичных цифр, что особенно хорошо подходит для реализации в высокоскоростных цифровых схемах.

Приближение выражается как $$|z|=\alpha \,\mathbf {Max} +\beta \,\mathbf {Min} ,$$где $\mathbf {Max}$ - максимальное абсолютное значение a и b , и $\mathbf {Min}$ — минимальное абсолютное значение a и b .

В ближайшем приближении оптимальные значения для $\alpha$ и $\beta$ являются $\alpha _{0}={\frac {2\cos {\frac {\pi }{8}}}{1+\cos {\frac {\pi }{8}}}}=0.960433870103...$ и $\beta _{0}={\frac {2\sin {\frac {\pi }{8}}}{1+\cos {\frac {\pi }{8}}}}=0.397824734759...$, что дает максимальную ошибку 3,96%.

$\alpha \,\!$	$\beta \,\!$	Самая большая ошибка (%)	Средняя ошибка (%)
1/1	1/2	11.80	8.68
1/1	1/4	11.61	3.20
1/1	3/8	6.80	4.25
7/8	7/16	12.50	4.91
15/16	15/32	6.25	3.08
$\alpha _{0}$	$\beta _{0}$	3.96	2.41

Улучшения

Когда $\alpha <1$, $|z|$ становится меньше, чем $\mathbf {Max}$ (что геометрически невозможно) вблизи осей, где $\mathbf {Min}$ находится рядом с 0.Это можно исправить, заменив результат на $\mathbf {Max}$ всякий раз, когда это значение больше, по сути, линия разделяется на два разных сегмента.

$|z|=\max(\mathbf {Max} ,\alpha \,\mathbf {Max} +\beta \,\mathbf {Min} ).$

В зависимости от оборудования это улучшение может быть практически бесплатным.

Использование этого улучшения меняет значения параметров, которые являются оптимальными, поскольку им больше не требуется точное совпадение на всем интервале. Нижний $\alpha$ и выше $\beta$ следовательно, может еще больше повысить точность.

Повышение точности: при разделении линии на две части можно еще больше повысить точность, заменив первый сегмент более точной оценкой, чем $\mathbf {Max}$и отрегулировать $\alpha$ и $\beta$ соответственно.

$|z|=\max {\big (}|z_{0}|,|z_{1}|{\big )},$

$|z_{0}|=\alpha _{0}\,\mathbf {Max} +\beta _{0}\,\mathbf {Min} ,$

$|z_{1}|=\alpha _{1}\,\mathbf {Max} +\beta _{1}\,\mathbf {Min} .$

$\alpha _{0}$	$\beta _{0}$	$\alpha _{1}$	$\beta _{1}$	Самая большая ошибка (%)
1	0	7/8	17/32	−2.65%
1	0	29/32	61/128	+2.4%
1	0	0.898204193266868	0.485968200201465	±2.12%
1	1/8	7/8	33/64	−1.7%
1	5/32	27/32	71/128	1.22%
127/128	3/16	27/32	71/128	−1.13%

Однако помните, что ненулевое $\beta _{0}$ потребуется как минимум одно дополнительное сложение и несколько битовых сдвигов (или умножение), что, вероятно, почти удвоит стоимость и, в зависимости от аппаратного обеспечения, возможно, вообще сведет на нет цель использования аппроксимации.

См. также

• Hypot — точная функция или алгоритм, который также защищен от переполнения и потери значения.

Ссылки

• Лайонс, Ричард Дж . Общие сведения о цифровой обработке сигналов, раздел 13.2. Прентис Холл, 2004 г. ISBN   0-13-108989-7 .
• Гриффин, Грант. Хитрость DSP: оценка величины .

Внешние ссылки

• «Расширение до трех измерений» . Обмен стеками . 14 мая 2015 г.