Изопериметрическая точка

В геометрии изопериметрическая точка — это центр треугольника — особая точка, связанная с плоским треугольником . Этот термин был первоначально введен Г. Р. Вельдкампом в статье, опубликованной в American Mathematical Monthly в 1985 году, для обозначения точки $P$ в плоскости треугольника $△ ABC,$ обладающей тем свойством, что треугольники $△ PBC, △ PCA, △ PAB$ имеют изопериметры, т. е. значит иметь свойство, которое ^[1]^[2]

${\begin{aligned}&{\overline {PB}}+{\overline {BC}}+{\overline {CP}},\\=\ &{\overline {PC}}+{\overline {CA}}+{\overline {AP}},\\=\ &{\overline {PA}}+{\overline {AB}}+{\overline {BP}}.\end{aligned}}$

Изопериметрические точки в смысле Вельдкампа существуют только для треугольников, удовлетворяющих определенным условиям. Изопериметрическая точка $△ ABC$ в смысле Вельдкампа, если она существует, имеет следующие трилинейные координаты . ^[3]

$\sec {\tfrac {A}{2}}\cos {\tfrac {B}{2}}\cos {\tfrac {C}{2}}-1\ :\ \sec {\tfrac {B}{2}}\cos {\tfrac {C}{2}}\cos {\tfrac {A}{2}}-1\ :\ \sec {\tfrac {C}{2}}\cos {\tfrac {A}{2}}\cos {\tfrac {B}{2}}-1$

Учитывая любой треугольник $△ ABC,$ ему можно сопоставить точку $P,$ имеющую трилинейные координаты, указанные выше. Эта точка является центром треугольника и в Кларка Кимберлинга ( Энциклопедии центров треугольников ETC) она называется изопериметрической точкой треугольника $△ ABC$ . Он обозначается как центр треугольника Х (175). ^[4] Точка X (175) не обязательно должна быть изопериметрической точкой треугольника $△ ABC$ в смысле Вельдкампа. Однако если бы изопериметрическая точка треугольника $△ ABC$ по Вельдкампу существовала, то она была бы идентична точке X (175).

Точка $Р,$ обладающая тем свойством, что треугольники $△ PBC, △ PCA, △ PAB$ имеют равные периметры, была изучена еще в 1890 году в статье Эмиля Лемуана . ^[4]^[5]

Существование изопериметрической точки по Вельдкампу.

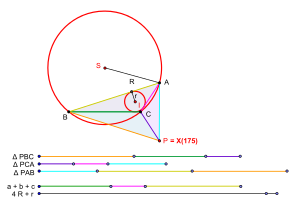
Пусть $△ ABC$ — любой треугольник. Пусть длины сторон этого треугольника равны $a, b, c$ . Пусть его радиус описанной окружности равен $R$ , а внутренний радиус равен $r$ . Необходимое и достаточное условие существования изопериметрической точки по Вельдкампу можно сформулировать следующим образом. ^[1]

Треугольник

△ ABC

имеет изопериметрическую точку по Вельдкампу тогда и только тогда, когда

a+b+c>4R+r.

Для всех остроугольных треугольников $△ ABC$ имеем $a + b + c > 4 R + r$ , и поэтому все остроугольные треугольники имеют изопериметрические точки в смысле Вельдкампа.

Характеристики

Обозначим через $P$ центр треугольника X (175) треугольника $△ ABC$ . ^[4]

$P$ лежит на линии, соединяющей центра и точку Жергонна △ $центр ABC$ .
Если $P$ — изопериметрическая точка $△ ABC$ в смысле Вельдкампа, то вписанные окружности треугольников $△ PBC, △ PCA, △ PAB$ попарно касаются друг друга, а $P$ — их радикальный центр.
Если $P$ — изопериметрическая точка $△ ABC$ в смысле Вельдкампа, то периметры $△ PBC, △ PCA, △ PAB$ равны

${\frac {2\triangle }{{\bigl |}4R+r-(a+b+c){\bigr |}}}$ где $△$ — площадь, $R$ — радиус описанной окружности, $r$ — внутренний радиус, а $a, b, c$ — длины сторон $△ ABC$ . ^[6]

Дерьмовые круги

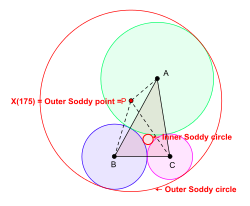
Учитывая треугольник $△ ABC,$ можно нарисовать в плоскости $△ ABC$ окружности с центрами в точках $A, B, C$ так, чтобы они внешне касались друг друга. В общем, можно нарисовать две новые окружности так, чтобы каждая из них касалась трех окружностей с $A, B, C.$ центрами (Один из кругов может выродиться в прямую линию.) Эти круги являются Содди △ $кругами ABC$ . Круг с меньшим радиусом — это внутренний круг Содди , а его центр называется внутренней точкой Содди или внутренним центром Содди $△ ABC$ . Круг с большим радиусом — это внешний круг Содди , а его центр называется внешней точкой Содди или внешним центром Содди треугольника $△ ABC$ . ^[6]^[7]

Центр треугольника X (175), изопериметрическая точка в смысле Кимберлинга, является внешней точкой Содди $△ ABC$ .

Ссылки

^ Jump up to: ^а ^б Г. Р. Вельдкамп (1985). «Изопериметрическая точка и точка (точки) равного обхода». амер. Математика. Ежемесячно . 92 (8): 546–558. дои : 10.2307/2323159 . JSTOR 2323159 .
^ Хаджа, Моваффак; Юфф, Питер (2007). «Изопериметрическая точка и точка (точки) равного обхода в треугольнике». Журнал геометрии . 87 (1–2): 76–82. дои : 10.1007/s00022-007-1906-y . S2CID 122898960 .
^ Кимберлинг, Кларк. «Изопериметрическая точка и равная точка объезда» . Проверено 27 мая 2012 г.
^ Jump up to: ^а ^б ^с Кимберлинг, Кларк. «X(175) Изопериметрическая точка» . Архивировано из оригинала 19 апреля 2012 года . Проверено 27 мая 2012 г.
^ Статью Эмиля Лемуана можно найти в Галлике. Статья начинается на странице 111, а этот вопрос обсуждается на странице 126. Gallica
^ Jump up to: ^а ^б Николаос Дергиадес (2007). «Дерзкие круги» (PDF) . Форум Геометрикорум . 7 : 191–197 . Проверено 29 мая 2012 г.
^ «Дерзкие круги» . Проверено 29 мая 2012 г.

Внешние ссылки

изопериметрические и равные точки объезда — интерактивная иллюстрация на Geogebratube

[Veldkamp-1] Jump up to: ^а ^б Г. Р. Вельдкамп (1985). «Изопериметрическая точка и точка (точки) равного обхода». амер. Математика. Ежемесячно . 92 (8): 546–558. дои : 10.2307/2323159 . JSTOR 2323159 .

[2] Хаджа, Моваффак; Юфф, Питер (2007). «Изопериметрическая точка и точка (точки) равного обхода в треугольнике». Журнал геометрии . 87 (1–2): 76–82. дои : 10.1007/s00022-007-1906-y . S2CID 122898960 .

[3] Кимберлинг, Кларк. «Изопериметрическая точка и равная точка объезда» . Проверено 27 мая 2012 г.

[ETC-4] Jump up to: ^а ^б ^с Кимберлинг, Кларк. «X(175) Изопериметрическая точка» . Архивировано из оригинала 19 апреля 2012 года . Проверено 27 мая 2012 г.

[5] Статью Эмиля Лемуана можно найти в Галлике. Статья начинается на странице 111, а этот вопрос обсуждается на странице 126. Gallica

[Dergi-6] Jump up to: ^а ^б Николаос Дергиадес (2007). «Дерзкие круги» (PDF) . Форум Геометрикорум . 7 : 191–197 . Проверено 29 мая 2012 г.

[7] «Дерзкие круги» . Проверено 29 мая 2012 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]