Дополняющий граф

В математической области теории графов дополнением , или обратным графом G H является граф H с одинаковыми вершинами что две различные вершины они смежны тогда и только тогда, когда не смежны в G. такой , То есть, чтобы сгенерировать дополнение графа, нужно заполнить все недостающие ребра, необходимые для формирования полного графа , и удалить все ребра, которые там были ранее. [1]
Дополнение не является заданным дополнением графа; дополняются только края.
Определение
[ редактировать ]Пусть G = ( V , E ) — простой граф и пусть K состоит из всех 2-элементных V. подмножеств Тогда H = ( V , K \ E ) является дополнением к G , [2] где K \ E — дополнение E K в . относительное Для ориентированных графов дополнение можно определить так же, как ориентированный граф на том же множестве вершин, используя набор всех 2-элементных упорядоченных пар V вместо набора K в формуле выше. С точки зрения матрицы смежности A графа , если Q — матрица смежности полного графа с одинаковым количеством вершин (т. е. все элементы равны единице, за исключением диагональных элементов, которые равны нулю), то матрица смежности дополнения А — это качество .
Дополнение не определено для мультиграфов . В графах, которые допускают циклы (но не множественные смежности), дополнение G может быть определено путем добавления цикла к каждой вершине, которая не имеет его в G , или в противном случае с использованием той же формулы, что и выше. Однако эта операция отличается от операции для простых графов, поскольку ее применение к графу без петель приведет к получению графа с петлями во всех вершинах.
Приложения и примеры
[ редактировать ]Несколько концепций теории графов связаны друг с другом посредством дополнения:
- Дополнением к графу без ребер является полный граф , и наоборот.
- Любой индуцированный подграф графа дополнений графа G является дополнением соответствующего индуцированного подграфа в G .
- Независимое множество в графе является кликой в графе дополнений и наоборот. Это частный случай двух предыдущих свойств, поскольку независимое множество представляет собой индуцированный подграф без ребер, а клика — полный индуцированный подграф.
- Группа автоморфизмов графа — это группа автоморфизмов его дополнения.
- Дополнением к каждому графу без треугольников является граф без клешней . [3] хотя обратное неверно.
Самодополняющие графы и классы графов
[ редактировать ]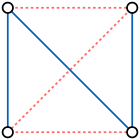
Самодополняющий граф — это граф, изоморфный своему дополнению. [1] с четырьмя вершинами Примеры включают граф путей с пятью вершинами и граф циклов . Не существует известной характеристики самодополняющих графов.
Некоторые классы графов являются самодополняющими в том смысле, что дополнением любого графа одного из этих классов является другой граф того же класса.
- Совершенные графы — это графы, в которых для каждого индуцированного подграфа хроматическое число равно размеру максимальной клики. Тот факт, что дополнение к совершенному графу также совершенно, является совершенном графе о теоремой Ласло Ловаса . [4]
- Кографы определяются как графы, которые могут быть построены из отдельных вершин с помощью операций непересекающегося объединения и дополнения. Они образуют самодополняющее семейство графов: дополнением к любому кографу является другой другой кограф. Для кографов с более чем одной вершиной связен ровно один граф в каждой дополнительной паре, и одно эквивалентное определение кографов состоит в том, что каждый из их связных индуцированных подграфов имеет несвязное дополнение. Другое, дополняющее себя определение, состоит в том, что это графы без индуцированного подграфа в форме пути с четырьмя вершинами. [5]
- Другой самодополняющий класс графов — это класс расщепляемых графов , графов, в которых вершины могут быть разделены на клику и независимое множество. Одно и то же разбиение дает независимый набор и клику в графе дополнений. [6]
- Пороговые графы — это графы, сформированные путем многократного добавления либо независимой вершины (одной, не имеющей соседей), либо универсальной вершины (смежной со всеми ранее добавленными вершинами). Эти две операции дополняют друг друга и создают самодополняющий класс графов. [7]
Алгоритмические аспекты
[ редактировать ]При анализе алгоритмов на графах различие между графом и его дополнением является важным, поскольку разреженный граф (с небольшим количеством ребер по сравнению с количеством пар вершин) вообще не будет иметь разреженного дополнения. , и поэтому алгоритм, который требует времени, пропорционального количеству ребер в данном графе, может занять гораздо большее количество времени, если тот же алгоритм запускается на явном представлении графа-дополнения. Поэтому исследователи изучили алгоритмы, которые выполняют стандартные графовые вычисления над дополнением входного графа, используя неявное представление графа , которое не требует явного построения графа-дополнения. В частности, можно смоделировать либо поиск в глубину, либо поиск в ширину на дополнительном графе за промежуток времени, который линейен по размеру данного графа, даже если дополнительный граф может иметь гораздо больший размер. . [8] Также возможно использовать эти симуляции для вычисления других свойств, касающихся связности графа дополнений. [8] [9]
Ссылки
[ редактировать ]- ^ Перейти обратно: а б Бонди, Джон Адриан ; Мурти, USR (1976), Теория графов с приложениями , Северная Голландия, стр. 6 , ISBN 0-444-19451-7 .
- ^ Дистель, Рейнхард (2005), Теория графов (3-е изд.), Springer , ISBN 3-540-26182-6 . Электронное издание , стр. 4.
- ^ Чудновская Мария ; Сеймур, Пол (2005), «Структура графов без когтей» (PDF) , Обзоры по комбинаторике 2005 г. , London Math. Соц. Лекционная конспект. Сер., т. 1, с. 327, Кембридж: Кембриджский университет. Пресс, стр. 153–171, МР 2187738 .
- ^ Ловас, Ласло (1972a), «Нормальные гиперграфы и гипотеза идеального графа», Discrete Mathematics , 2 (3): 253–267, doi : 10.1016/0012-365X(72)90006-4 .
- ^ Корней, Д.Г. ; Лерхс, Х.; Стюарт Берлингэм, Л. (1981), «Дополнительные приводимые графы», Discrete Applied Mathematics , 3 (3): 163–174, doi : 10.1016/0166-218X(81)90013-5 , MR 0619603 .
- ^ Голумбик, Мартин Чарльз (1980), Алгоритмическая теория графов и совершенные графы , Academic Press, теорема 6.1, стр. 150, ISBN 0-12-289260-7 , МР 0562306 .
- ^ Голумбик, Мартин Чарльз; Джеймисон, Роберт Э. (2006), «Классы графов с ранговой толерантностью», Journal of Graph Theory , 52 (4): 317–340, doi : 10.1002/jgt.20163 , MR 2242832 .
- ^ Перейти обратно: а б Ито, Хиро; Ёкояма, Мицуо (1998), «Алгоритмы линейного времени для поиска графов и определения связности на дополнительных графах», Information Processing Letters , 66 (4): 209–213, doi : 10.1016/S0020-0190(98)00071-4 , MR 1629714 .
- ^ Као, Мин-Ян; Оккиогроссо, Нил; Тенг, Шан-Хуа (1999), «Простые и эффективные схемы сжатия графов для плотных и дополнительных графов», Journal of Combinatorial Optimization , 2 (4): 351–359, doi : 10.1023/A:1009720402326 , MR 1669307 .