Мучнистая машина

В теории вычислений машина Мили — это конечный автомат , выходные значения которого определяются как его текущим состоянием , так и текущими входными данными. В этом отличие от машины Мура , выходные значения которой определяются исключительно ее текущим состоянием. Машина Мили — это детерминированный преобразователь с конечным состоянием : для каждого состояния и входа возможен не более одного перехода.

История [ править ]

Машина Мили названа в честь Джорджа Мили , который представил эту концепцию в статье 1955 года «Метод синтеза последовательных схем». ^[1]

Формальное определение [ править ]

Машина Мили представляет собой шестикортежную $(S,S_{0},\Sigma ,\Lambda ,T,G)$ состоящий из следующего:

конечное множество состояний $S$
начальное состояние (также называемое начальным состоянием) $S_{0}$ который является элементом $S$
конечное множество, называемое входным алфавитом $\Sigma$
конечный набор, называемый выходным алфавитом $\Lambda$
перехода функция $T:S\times \Sigma \rightarrow S$ отображение пар состояния и входного символа в соответствующее следующее состояние.
выходная функция $G:S\times \Sigma \rightarrow \Lambda$ отображение пар состояния и входного символа на соответствующий выходной символ.

В некоторых формулировках функции перехода и вывода объединены в одну функцию. $T:S\times \Sigma \rightarrow S\times \Lambda$ .

машин Мили и Сравнение машин Мура

Машины Мили, как правило, имеют меньше состояний:
- Различные выходы на дугах ( n ²), а не состояния ( n ).
Машины Мура безопаснее использовать:
- Выходные сигналы изменяются по фронту тактового сигнала (всегда на один цикл позже).
- В машинах Мили изменение входных данных может привести к изменению выходных данных, как только будет выполнена логика — большая проблема, когда две машины соединены между собой — может возникнуть асинхронная обратная связь, если не соблюдать осторожность.
Машины Мили быстрее реагируют на входные данные:
- Реагируйте в том же цикле — им не нужно ждать часов.
- В машинах Мура для декодирования состояния на выходы может потребоваться больше логики — больше задержек на логическом элементе после фронта тактового сигнала.

Диаграмма [ править ]

Диаграмма состояний машины Мили связывает выходное значение с каждым ребром перехода, в отличие от диаграммы состояний машины Мура, которая связывает выходное значение с каждым состоянием.

Когда входной и выходной алфавит являются $Σ$ , автомату Мили также можно сопоставить спирально- ориентированный граф. ^{[ нужны разъяснения ]} $(S \times Σ, (Икс, я) \to (Т (Икс, я), грамм (Икс, я)))$ . ^[2] В этом графе вершинами являются пары состояний и букв, каждый узел имеет исходящую степень один, а преемник $(x, i)$ является следующим состоянием автомата и буквой, которую автомат выводит, когда он находится в состоянии $x$ и он читает букву $i$ . Этот граф является объединением непересекающихся циклов, если автомат двуобратим. ^{[ необходимо определение ]}.

Примеры [ править ]

Просто [ править ]

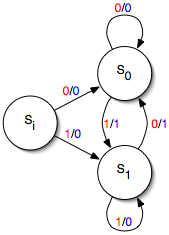
Диаграмма состояний простого автомата Мили с одним входом и одним выходом. (Для каждого входного значения выводится 1, если текущее входное значение отличается от предыдущего, или 0 в противном случае.)

Простая машина Мили имеет один вход и один выход. Каждый край перехода помечен значением входа (показано красным) и значением выхода (показано синим). Машина запускается в состоянии $S i$ . (В этом примере выходные данные представляют собой исключающее ИЛИ из двух самых последних входных значений; таким образом, машина реализует детектор границ, выдавая 1 каждый раз, когда входные данные переворачиваются, и 0 в противном случае.)

Комплекс [ править ]

Более сложные машины Мили могут иметь как несколько входов, так и несколько выходов. ^{[ нужна ссылка ]}

Приложения [ править ]

Машины Мили представляют собой элементарную математическую модель шифровальных машин. Если принять во внимание входной и выходной алфавит (например, латинский алфавит ), то можно спроектировать машину Мили, которая сможет преобразовать заданную строку букв (последовательность входных данных) в зашифрованную строку (последовательность выходных данных). можно использовать модель Мили Однако, хотя для описания «Энигмы» , диаграмма состояний была бы слишком сложной, чтобы обеспечить возможные средства проектирования сложных шифровальных машин.

Машины Мура/Мили — это DFA , которые также выдают результаты в любой такт. Современные процессоры, компьютеры, сотовые телефоны, цифровые часы и базовые электронные устройства/машины имеют своего рода конечный автомат для управления ими.

Простые программные системы, особенно те, которые могут быть представлены с помощью регулярных выражений , можно моделировать как конечные автоматы. Существует множество таких простых систем, таких как торговые автоматы или базовая электроника.

Найдя пересечение двух конечных автоматов, можно очень просто спроектировать параллельные системы , которые, например, обмениваются сообщениями. Например, светофор — это система, состоящая из нескольких подсистем, таких как различные светофоры, которые работают одновременно.

Некоторые примеры приложений:

Классификация номеров
смотреть с таймером
торговый автомат
светофор
сканер штрих-кода
газовые насосы

См. также [ править ]

Сноски [ править ]

^ Мили, Джордж Х. (сентябрь 1955 г.). «Метод синтеза последовательных цепей». Технический журнал Bell System . 34 (5): 1045–1079. дои : 10.1002/j.1538-7305.1955.tb03788.x .
^ Ахави и др. (2012)

Ссылки [ править ]

Мили, Джордж Х. (1955). Метод синтеза последовательных цепей . Технический журнал Bell System. стр. 1045–1079.
Холкомб, WML (1982). Алгебраическая теория автоматов . Кембриджские исследования по высшей математике. Том. 1. Издательство Кембриджского университета . ISBN 0-521-60492-3 . Збл 0489.68046 .
Рот, Чарльз Х. младший (2004). Основы логического проектирования . Томсон-Инжиниринг. стр. 364–367. ISBN 0-534-37804-8 .
Ахави, Али; Климанн, Инес; Ломбардия, Сильвен; Мерес, Жан; Пикантен, Матье (2012). «К проблеме конечности автоматных (полу)групп». Международный журнал алгебры и вычислений . 22 (6). arXiv : 1105.4725 . Бибкод : 2011arXiv1105.4725A . дои : 10.1142/S021819671250052X . S2CID 47518684 . Збл 1280.20038 .

Внешние ссылки [ править ]

СМИ, связанные с машиной Мили, на Викискладе?

[1] Мили, Джордж Х. (сентябрь 1955 г.). «Метод синтеза последовательных цепей». Технический журнал Bell System . 34 (5): 1045–1079. дои : 10.1002/j.1538-7305.1955.tb03788.x .

[2] Ахави и др. (2012)

[1]

[2]