Оптимизация компоновки разрывов

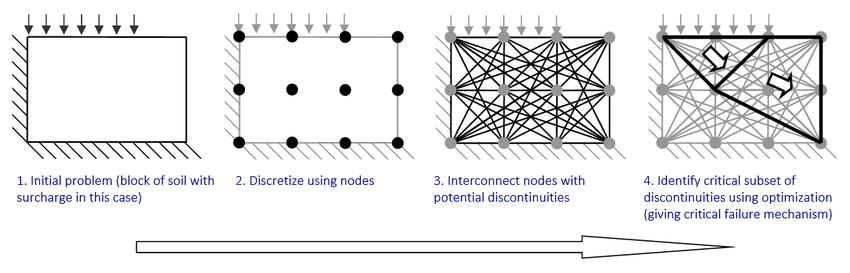
Оптимизация компоновки несплошностей (DLO) — это процедура инженерного анализа , которую можно использовать для непосредственного определения величины нагрузки , которую может нести твердое тело или конструкция до разрушения. С помощью DLO расположение плоскостей разрушения или «разрывов» в разрушающемся твердом теле или конструкции определяется с использованием методов математической оптимизации (отсюда и название «оптимизация расположения несплошностей»). Предполагается, что разрушение происходит пластичным или « пластическим » образом.
Как это работает
[ редактировать ]Процедура DLO включает в себя ряд шагов, как описано ниже.
Набор потенциальных разрывов может включать разрывы, которые пересекаются друг с другом, что позволяет идентифицировать сложные схемы отказов (например, с использованием «веерных» механизмов, когда множество разрывов расходятся из одной точки).
ДЛО можно сформулировать в терминах равновесных отношений («статическая» формулировка) или в терминах перемещений («кинематическая» формулировка). В последнем случае целью задачи математической оптимизации является минимизация внутренней энергии, рассеиваемой вдоль разрывов, с учетом узловых ограничений совместимости. Эту проблему можно решить, используя эффективные методы линейного программирования , а в сочетании с алгоритмом, первоначально разработанным для задач оптимизации компоновки ферм, [1] Было обнаружено, что современные компьютерные мощности можно использовать для прямого поиска среди очень большого количества различных топологий механизмов отказа (примерно до 2). 1,000,000,000 различные топологии на ПК текущего поколения). Полное описание применения DLO к задачам плоской деформации было предоставлено Смитом и Гилбертом. [2] анализу каменной арки, проведенному Гилбертом и др., [3] для решения проблем с плитами Гилберта и др., [4] [5] [6] и к 3D-задачам Хоксби и др., [7] и Чжан. [8]
ДЛО против ФЕМ
[ редактировать ]В то время как с помощью анализа методом конечных элементов (МКЭ), широко используемой альтернативной процедуры инженерного анализа , математические соотношения формируются для основной задачи механики сплошной среды , DLO включает в себя анализ потенциально гораздо более простой проблемы разрыва, при этом проблема ставится полностью с точки зрения индивидуального подхода. разрывы, которые соединяют узлы, расположенные поперек рассматриваемого тела. Кроме того, когда для анализа состояния коллапса используются универсальные программы конечных элементов, часто относительно сложные нелинейные требуются решатели, в отличие от более простых решателей линейного программирования, обычно необходимых в случае DLO.
По сравнению с нелинейным МКЭ, ДЛО имеет следующие преимущества и недостатки:
Преимущества
- Состояние коллапса анализируется напрямую, без необходимости выполнения итераций. Это означает, что решения обычно можно получить гораздо быстрее.
- Выходные данные в виде анимированных механизмов отказа обычно легче интерпретировать.
- Проблемы, связанные с сингулярностями в полях напряжений или перемещений, можно решить без труда.
- Поскольку DLO намного проще, чем нелинейный FEM, пользователям требуется меньше обучения для эффективного использования этого метода.
Недостатки
- Как и другие методы анализа пределов , DLO не предоставляет информации о смещениях (или напряжениях) до разрушения.
- DLO фундаментально основан на моделировании совместимых механизмов обрушения почвы и, следовательно, является методом верхней границы . В результате метод всегда будет прогнозировать неконсервативную разрушающую нагрузку.
- Хотя схемы оптимизации схемы разрывов и линейного программирования, используемые в DLO, обычно гарантируют, что будет найдена хорошая аппроксимация истинного механизма разрушения, невозможно определить, насколько прогнозируемая нагрузка разрушения превысит истинную нагрузку разрушения без сравнения с независимый анализ нижней границы .
- DLO — относительно новый метод, поэтому в настоящее время доступен лишь ограниченный набор программных инструментов.
Приложения
[ редактировать ]DLO, пожалуй, наиболее полезно применять для инженерных задач, где традиционные ручные вычисления сложны или слишком упрощают задачу, но где обращение к более сложным нелинейным МКЭ не оправдано. Приложения включают в себя:
- Анализ инженерно-геологических проблем (например, устойчивость склонов , несущая способность [9] или проблемы с подпорной стеной ).
- Анализ проблем с бетонными плитами .
- Анализ проблем обработки металлов давлением или экструзии .
Программное обеспечение, использующее оптимизацию схемы разрывов
[ редактировать ]- Сценарий MATLAB (2009 г.) Предоставлен исследовательской группой CMD в Университете Шеффилда, Великобритания.
- LimitState:GEO (2008-) Геотехническое программное обеспечение общего назначения.
- LimitState:SLAB (2015-) Программное обеспечение для анализа плит.
Ссылки
[ редактировать ]- ^ Гилберт М. и Тайас А. (2003) Оптимизация компоновки крупномасштабных шарнирных рам, Engineering Computations, Vol. 20, № 8, стр.1044-1064
- ^ Смит, К.С. и Гилберт, М. (2007) Применение оптимизации расположения разрывов для решения плоских задач пластичности, Proc. Королевское общество А, том 463, номер 2086, стр. 2461–2484.
- ^ Гилберт, М., Смит, К.С. и Причард, Т.Дж. (2010) Анализ каменной арки с использованием оптимизации компоновки разрывов. ДВС-инжиниринг и вычислительная механика, том 163, стр. 167-178.
- ^ Гилберт, М., Хе, Л., Смит, К.С. и Ле, К.В. (2014) Автоматический анализ линии текучести плит с использованием оптимизации схемы разрывов. Труды Королевского общества A, том 470, статья 20140071.
- ^ Хе, Л., Гилберт, М. и Шепард, М. (2017) Автоматический анализ линии текучести практических конфигураций плит посредством оптимизации схемы разрывов. Журнал структурного проектирования, DOI: 10.1061/(ASCE) ST.1943-541X.0001700
- ^ Хе, Л. и Гилберт, М. (2016) Автоматическая рационализация моделей линий текучести, выявленных с помощью оптимизации компоновки разрывов. Международный журнал твердых тел и структур, том 84, стр. 27-39.
- ^ Хоксби, С., Смит, К.С. и Гилберт, М. (2013) Применение оптимизации компоновки разрывов к трехмерным задачам пластичности. Труды Королевского общества A, том 469, статья 20130009.
- ^ Чжан, Ю. (2017) Стратегия мультисрезов для оптимизации трехмерной компоновки разрывов (3D DLO). Международный журнал численных и аналитических методов в геомеханике, том 41, стр. 488-507.
- ^ Ли, Ю.С., Смит К.С. и Чеук С.Ю. (2008) Несущая способность закладных фундаментов. На 2-й Международной конференции по фондам, ICOF 2008, Данди, стр. 961–972.
Внешние ссылки
[ редактировать ]- Учебные ресурсы DLO , предоставленные Группой геотехнических инженерных исследований Университета Шеффилда, Великобритания.