Спиральное подобие

Спиральное подобие — это плоское преобразование в математике, состоящее из вращения и расширения . ^[1] Он широко используется в евклидовой геометрии для облегчения доказательства многих теорем и других результатов в геометрии, особенно на математических соревнованиях и олимпиадах. Хотя происхождение этой идеи неизвестно, она была задокументирована в 1967 году Коксетером в его книге «Возвращение к геометрии» . ^[2] и 1969 — используя термин «дилативное вращение» — в своей книге « Введение в геометрию» . ^[3]

следующая теорема : Для евклидовой плоскости важна
Любые две непосредственно подобные фигуры связаны либо сдвигом, либо спиральным подобием. ^[4]
(Подсказка: Непосредственно подобные фигуры похожи и имеют одинаковую ориентацию)

Определение

Спиральное подобие $S$ состоит из вращения плоскости с последующим расширением вокруг центра $O$ с координатами $c$ в самолете. ^[5] Выражение вращения линейным преобразованием $T(x)$ а расширение как умножение на масштабный коэффициент $d$ , точка $p$ сопоставляется с $S(p)=d(T(p-c))+c.$

На комплексной плоскости любое спиральное подобие можно выразить в виде $T(x)=x_{0}+\alpha (x-x_{0})$ , где $\alpha$ это комплексное число . Величина $|\alpha |$ – коэффициент расширения спирального подобия, а аргумент ${\text{arg}}(\alpha )$ это угол поворота. ^[6]

Характеристики

Два круга

Пусть T — спиральный круг отображения подобия k в k' с k $\cap$ k' = {C, D} и неподвижная точка C.

Тогда для каждой точки P $\in$ k точки P, T(P) = P' и D лежат на одной прямой.

Примечание: Это свойство является основой построения центра спирального подобия для двух отрезков.

Доказательство:

$\angle CMP=\angle CM'P'$ , поскольку вращение и расширение сохраняют углы.

$\angle P'DC+\angle CDP=180^{\circ }$ , как если бы радиус ${\overline {MD}}$ пересекает хорду ${\overline {CP}}$ , затем ${\overline {M'D}}$ не встречается ${\overline {CP'}}$ , и если ${\overline {MD}}$ не пересекается ${\overline {CP}}$ , затем ${\overline {M'D}}$ пересекает ${\overline {CP'}}$ , поэтому один из этих углов равен $\beta$ а другой $180^{\circ }-\beta$ .

Итак, P, P' и D лежат на одной прямой.

Центр подобия спирали для двух отрезков

Посредством расширения линии, вращения и перемещения любой сегмент линии может быть преобразован в любой другой посредством серии преобразований плоскости. Центр подобия спирали можно найти с помощью следующей конструкции: ^[1]

Рисовать линии ${\overline {AC}}$ и ${\overline {BD}}$ , и пусть $P$ быть пересечением двух прямых.
Нарисуйте окружности треугольников $\triangle PAB$ и $\triangle PCD$ .
Описанные окружности пересекаются во второй точке $X\neq P$ . Затем $X$ это отображение центра спирали ${\overline {AB}}$ к ${\overline {CD}}.$

Доказательство: Обратите внимание, что $ABPX$ и $XPCD$ являются вписанными четырёхугольниками . Таким образом, $\angle XAB=180^{\circ }-\angle BPX=\angle XPD=\angle XCD$ . Сходным образом, $\angle ABX=\angle APX=180^{\circ }-\angle XPC=\angle XDC$ . Следовательно, по AA-подобию треугольники $XAB$ и $XCD$ похожи. Таким образом, $\angle AXB=\angle CXD,$ поэтому отображение угла поворота $A$ к $B$ также карты $C$ к $D$ . Тогда коэффициент расширения представляет собой просто соотношение длин сторон. ${\overline {CD}}$ к ${\overline {AB}}$ . ^[5]

Решение с комплексными числами

Если мы выражаем $A,B,C,$ и $D$ как точки на комплексной плоскости с соответствующими комплексными числами $a,b,c,$ и $d$ , мы можем найти выражение спирального подобия, которое принимает $A$ к $C$ и $B$ к $D$ . Обратите внимание, что $T(a)=x_{0}+\alpha (a-x_{0})$ и $T(b)=x_{0}+\alpha (b-x_{0})$ , так ${\frac {T(b)-T(a)}{b-a}}=\alpha$ . С $T(a)=c$ и $T(b)=d$ , мы подключаемся, чтобы получить $\alpha ={\frac {d-c}{b-a}}$ , откуда мы получаем $x_{0}={\frac {ad-bc}{a+d-b-c}}$ . ^[5]

Пары спиральных подобий

По любым пунктам $A,B,C,$ и $D$ , центр спирального подобия принимая ${\overline {AB}}$ к ${\overline {CD}}$ также является центром спирального подобия, принимающего ${\overline {AC}}$ к ${\overline {BD}}$ .

Это видно по приведенной выше конструкции. Если мы позволим $X$ быть центром спирального подобия, принимая ${\overline {AB}}$ к ${\overline {CD}}$ , затем $\triangle XAB\sim \triangle XCD$ . Поэтому, $\angle AXC=\angle AXB+\angle BXC=\angle CXD+\angle BXC=\angle BXD$ . Также, ${\frac {AX}{BX}}={\frac {CX}{DX}}$ подразумевает, что ${\frac {AX}{CX}}={\frac {BX}{DX}}$ . Итак, по сходству SAS мы видим, что $\triangle AXC\sim \triangle BXD$ . Таким образом $X$ также является центром спирального подобия, которое принимает ${\overline {AC}}$ к ${\overline {BD}}$ . ^[5]^[6]

Следствия

Доказательство теоремы Микеля о четырехугольнике.

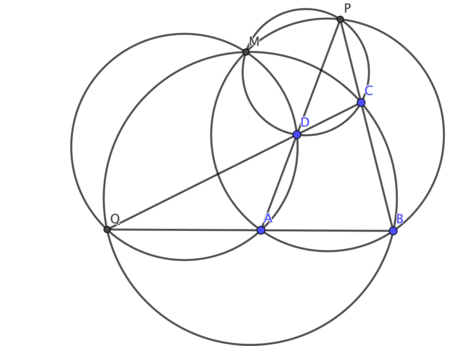
Спиральное подобие можно использовать для доказательства теоремы Микеля о четырехугольниках : даны четыре неколлинеарные точки. $A,B,C,$ и $D$ , описанные окружности четырех треугольников $\triangle PAB,\triangle PDC,\triangle QAD,$ и $\triangle QBC$ пересекаются в одной точке, где $P$ является пересечением $AD$ и $BC$ и $Q$ является пересечением $AB$ и $CD$ (см. схему). ^[1]

Позволять $M$ быть центром спирального подобия, которое принимает $AB$ к $DC$ . По вышеприведенному построению описанные окружности $\triangle PAB$ и $\triangle PDC$ пересекаться в $M$ и $P$ . С $M$ также является центром спирального подобия, принимая $DA$ к $BC$ , по аналогичным рассуждениям описанные окружности $\triangle QAD$ и $\triangle QBC$ встретиться в $Q$ и $M$ . Таким образом, все четыре окружности пересекаются в точке $M$ . ^[1]

Пример проблемы

Вот пример задачи на финале МО в Японии 2018 года, которую можно решить с помощью спирального подобия:

Дан разносторонний треугольник $ABC$ , позволять $D$ и $E$ быть точками на отрезках $AB$ и $AC$ соответственно, так что $CA=CD,BA=BE$ . Позволять $\omega$ быть описанной окружностью треугольника $ADE$ и $P$ отражение $A$ через $BC$ . Линии $PD$ и $PE$ встретиться $\omega$ снова в $X$ и $Y$ , соответственно. Докажите, что $BX$ и $CY$ пересекаться на $\omega$ . ^[5]

Доказательство. Сначала мы докажем следующие утверждения:

Пункт 1 : Четырехугольник. $PBEC$ является циклическим.

Доказательство: поскольку $\triangle BAE$ равнобедренная, заметим, что $\angle BPC=\angle BAC=180^{\circ }-\angle BEC,$ тем самым доказав, что четырёхугольник $PBEC$ является циклическим, как и хотелось. Используя симметрию, мы можем доказать, что четырехугольник $PBDC$ является циклическим.

Претензия 2 : $\triangle AXY\sim \triangle ABC.$

Доказательство: у нас есть это $\angle AXY=180^{\circ }-\angle AEY=\angle YEC=\angle PEC=\angle PBC=\angle ABC.$ По аналогичным рассуждениям $\angle AYX=\angle ACB,$ так что по сходству АА, $\triangle AXY\sim \triangle ABC,$ по желанию.

Теперь мы отмечаем, что $A$ это спиральный центр, который отображает $XY$ к $BC$ . Позволять $F$ быть пересечением $BX$ и $CY$ . Согласно приведенной выше конструкции подобия спирали, центр спирали должен быть пересечением описанных окружностей. $\triangle FXY$ и $\triangle FBC$ . Однако этот момент $A$ , поэтому точки $A,F,X,Y$ должен быть конциклическим. Следовательно, $F$ должен лежать на $\omega$ , по желанию.

Ссылки

^ Jump up to: Перейти обратно: ^а ^б ^с ^д Чен, Эван (2016). Евклидова геометрия в математических олимпиадах . США: МАА Пресс. стр. 196–200. ISBN 978-0-88385-839-4 .
^ Коксетер, HSM (1967). Возвращение к геометрии . Торонто и Нью-Йорк: Математическая ассоциация Америки. стр. 95–100 . ISBN 978-0-88385-619-2 .
^ Коксетер, HSM (1969). Введение в геометрию (2-е изд.). Нью-Йорк, Лондон, Сидней и Торонто: John Wiley & Sons. стр. 72–75.
^ Коксетер, HSM (1967). Возвращение к геометрии . Математическая ассоциация Америки. п. 97]. ISBN 978-0-88385-619-2 .
^ Jump up to: Перейти обратно: ^а ^б ^с ^д ^и Бака, Джафет (2019). «Об особом центре спирального подобия». Математические размышления . 1 :1–9.
^ Jump up to: Перейти обратно: ^а ^б Чжао, Ю. (2010). Три леммы по геометрии . См. также Решения

[:0-1] Jump up to: Перейти обратно: ^а ^б ^с ^д Чен, Эван (2016). Евклидова геометрия в математических олимпиадах . США: МАА Пресс. стр. 196–200. ISBN 978-0-88385-839-4 .

[2] Коксетер, HSM (1967). Возвращение к геометрии . Торонто и Нью-Йорк: Математическая ассоциация Америки. стр. 95–100 . ISBN 978-0-88385-619-2 .

[3] Коксетер, HSM (1969). Введение в геометрию (2-е изд.). Нью-Йорк, Лондон, Сидней и Торонто: John Wiley & Sons. стр. 72–75.

[4] Коксетер, HSM (1967). Возвращение к геометрии . Математическая ассоциация Америки. п. 97]. ISBN 978-0-88385-619-2 .

[:1-5] Jump up to: Перейти обратно: ^а ^б ^с ^д ^и Бака, Джафет (2019). «Об особом центре спирального подобия». Математические размышления . 1 :1–9.

[:2-6] Jump up to: Перейти обратно: ^а ^б Чжао, Ю. (2010). Три леммы по геометрии . См. также Решения

[1]

[2]

[3]

[4]

[5]

[6]