Круговое преобразование Хафа
| Обнаружение функций |
|---|
| Обнаружение края |
| Обнаружение угла |
| Обнаружение больших двоичных объектов |
| Обнаружение гребней |
| Преобразование Хафа |
| Тензор структуры |
| Обнаружение аффинных инвариантных функций |
| Описание функции |
| Масштабировать пространство |
( Преобразование Хафа круга CHT ) — это базовый метод выделения признаков , используемый при цифровой обработке изображений для обнаружения кругов на несовершенных изображениях. Кандидаты в круг создаются путем «голосования» в пространстве параметров Хафа и последующего выбора локальных максимумов в матрице -аккумуляторе .
Это специализация преобразования Хафа .
Теория
[ редактировать ]В двумерном пространстве круг можно описать следующим образом:
где (a,b) — центр круга, а r — радиус . Если 2D-точка (x,y) фиксирована, то параметры можно найти согласно (1). Пространство параметров будет трехмерным (a, b, r). И все параметры, удовлетворяющие (x, y), будут лежать на поверхности перевернутого прямоугольного конуса, вершина которого находится в точке (x, y, 0). В трехмерном пространстве параметры окружности можно определить по пересечению множества конических поверхностей, которые определяются точками на двумерной окружности. Этот процесс можно разделить на два этапа. Первый этап — определение радиуса, затем поиск оптимального центра кругов в двумерном пространстве параметров. Второй этап – поиск оптимального радиуса в одномерном пространстве параметров.
Найти параметры с известным радиусом R
[ редактировать ]Если радиус фиксирован, то пространство параметров будет уменьшено до 2D (положение центра круга). Для каждой точки (x, y) исходной окружности можно определить окружность с центром в точке (x, y) и радиусом R согласно (1). Точка пересечения всех таких кругов в пространстве параметров будет соответствовать центральной точке исходного круга.
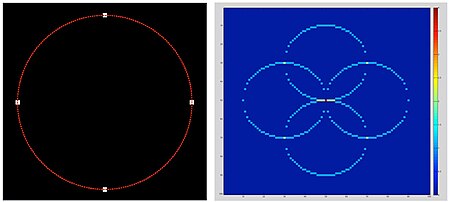
Рассмотрим 4 точки окружности на исходном изображении (слева). Круговое преобразование Хафа показано справа. Обратите внимание, что радиус предполагается известным. Для каждой (x,y) из четырех точек (белых точек) исходного изображения он может определить круг в пространстве параметров Хафа с центром в (x, y) и радиусом r. Матрица аккумулятора используется для отслеживания точки пересечения. В пространстве параметров голосующее количество точек, через которые проходит круг, будет увеличено на одну. Затем можно найти точку локального максимума (красная точка в центре на правом рисунке). Положение (a, b) максимумов будет центром исходного круга.
Несколько кругов с известным радиусом R
[ редактировать ]С помощью одной и той же техники можно найти несколько кругов одинакового радиуса.

Обратите внимание, что в матрице аккумулятора (рис. справа) будет как минимум 3 точки локального максимума.
Матрица аккумуляторов и голосование
[ редактировать ]На практике матрица-накопитель вводится для поиска точки пересечения в пространстве параметров. Во-первых, нам нужно разделить пространство параметров на «корзины» с помощью сетки и создать матрицу аккумулятора в соответствии с сеткой. Элемент в матрице аккумулятора обозначает количество «кругов» в пространстве параметров, которые проходят через соответствующую ячейку сетки в пространстве параметров. Этот номер еще называют «номером для голосования». Изначально каждый элемент матрицы равен нулю. Затем для каждой «краевой» точки в исходном пространстве мы можем сформулировать круг в пространстве параметров и увеличить число голосований ячейки сетки, через которую проходит круг. Этот процесс называется «голосованием».
После голосования мы можем найти локальные максимумы в матрице аккумулятора. Положения локальных максимумов соответствуют центрам окружностей в исходном пространстве.
Найти параметр окружности с неизвестным радиусом
[ редактировать ]Поскольку пространство параметров трехмерное, матрица аккумулятора тоже будет трехмерной. Мы можем перебирать возможные радиусы; для каждого радиуса мы используем предыдущую технику. Наконец, найдите локальные максимумы в матрице трехмерного аккумулятора. Массив аккумуляторов должен иметь вид A[x,y,r] в трехмерном пространстве. Голосование должно проводиться за каждый пиксель, радиус и тету A[x,y,r] += 1
Алгоритм:
- Для каждого A[a,b,r] = 0;
- Обработайте алгоритм фильтрации изображения по Гауссу, преобразуйте изображение в оттенки серого (grayScaling), создайте оператор Canny . Оператор Canny придает края изображению.
- Голосуйте за все возможные круги в аккумуляторе.
- Локальные максимальные проголосовавшие круги аккумулятора А дают кругу пространство Хафа.
- Максимальный проголосованный круг аккумулятора дает круг.
Надбавка за лучшего кандидата:
For each A[a,b,r] = 0; // fill with zeroes initially, instantiate 3D matrix
For each cell(x,y)
For each theta t = 0 to 360 // the possible theta 0 to 360
b = y – r * sin(t * PI / 180); //polar coordinate for center (convert to radians)
a = x – r * cos(t * PI / 180); //polar coordinate for center (convert to radians)
A[a,b,r] +=1; //voting
end
end
Примеры
[ редактировать ]Найдите круги на отпечатке обуви
[ редактировать ]Исходное изображение (справа) сначала преобразуется в двоичное изображение (слева) с использованием порогового значения и фильтра Гаусса. Затем из него находятся края (середина) с помощью обнаружения хитрых краев . После этого все краевые точки используются преобразованием Хафа круга для поиска базовой структуры круга.
Ограничения
[ редактировать ]Поскольку пространство параметров CHT трехмерно, оно может потребовать большого объема памяти и вычислений. Выбор большего размера сетки может решить эту проблему.
Однако выбрать подходящий размер сетки сложно. Поскольку слишком грубая сетка может привести к ошибочному получению больших значений голосов, поскольку одному ведру соответствует множество совершенно разных структур. Слишком мелкая сетка может привести к тому, что структуры не будут найдены, поскольку голоса, полученные от токенов, которые не совсем выровнены, попадают в разные корзины, и ни одна корзина не имеет большого количества голосов.
Кроме того, CHT не очень устойчив к шуму.
Расширения
[ редактировать ]Адаптивное преобразование Хафа
[ редактировать ]Дж. Иллингворт и Дж. Киттлер [ 1 ] представил этот метод для эффективной реализации преобразования Хафа. AHT использует небольшой аккумуляторный массив и идею гибкой итеративной стратегии накопления и поиска «от грубого до точного» для выявления значительных пиков в пространствах параметров Хафа. Этот метод существенно превосходит стандартную реализацию преобразования Хафа как по требованиям к хранению, так и по вычислительным ресурсам.
Приложение
[ редактировать ]Подсчет людей
[ редактировать ]Поскольку голова на изображении будет похожа на круг, CHT можно использовать для обнаружения голов на изображении и подсчета количества людей на изображении. [ 2 ]
Обнаружение аневризмы головного мозга
[ редактировать ]Модифицированное преобразование круга Хафа (MHCT) используется на изображении, извлеченном из цифровой субтракционной ангиограммы (DSA), для обнаружения и классификации типа аневризмы.
Код реализации
[ редактировать ]- Обнаружение круга с помощью стандартного преобразования Хафа , автор Амин Сарафраз, Mathworks (обмен файлами)
- Hough Circle Transform , Учебные пособия по OpenCV-Python (архивная версия на archive.org)
См. также
[ редактировать ]- Преобразование Хафа
- Обобщенное преобразование Хафа
- Рандомизированное преобразование Хафа
- Лекция 10: Преобразование круга Хафа , Харви Роди, Центр обработки изображений Честера Ф. Карлсона, Рочестерский технологический институт (11 октября 2005 г.)
Ссылки
[ редактировать ]- ^ Дж. Иллингворт и Дж. Киттлер, «Адаптивное преобразование Хафа», PAMI-9, выпуск: 5, 1987, стр. 690-698.
- ^ Хун Лю, Юэлян Цянь и Шоусунь Линь, «ОБНАРУЖЕНИЕ ЛЮДЕЙ С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ КРУГА ХАФА В ВИДЕО НАБЛЮДЕНИЯ»
- ^ Митра, Джубин и др. эл. «Поход на вершину горы иерархии для обнаружения церебральной аневризмы с использованием модифицированного преобразования круга Хафа». Электронные письма ELVCIA по компьютерному зрению и анализу изображений 12.1 (2013). http://elcvia.cvc.uab.es/article/view/v12-n1-mitra-chandra-halder