Оптимизация топологии

Оптимизация топологии — это математический метод, который оптимизирует расположение материалов в заданном пространстве проектирования для заданного набора нагрузок , граничных условий и ограничений с целью максимизации производительности системы. Оптимизация топологии отличается от оптимизации формы и оптимизации размеров в том смысле, что проект может принять любую форму в пространстве дизайна, вместо того, чтобы иметь дело с предопределенными конфигурациями.

Традиционная формулировка оптимизации топологии использует метод конечных элементов (МКЭ) для оценки характеристик конструкции. Конструкция оптимизируется с использованием либо методов математического программирования на основе градиента , таких как алгоритм критериев оптимальности и метод перемещения асимптот , либо алгоритмов, не основанных на градиенте, таких как генетические алгоритмы .

Оптимизация топологии имеет широкий спектр применений в аэрокосмической, механической, биохимической и гражданской инженерии. В настоящее время инженеры в основном используют оптимизацию топологии на концептуальном уровне процесса проектирования . Из-за свободных форм, которые встречаются в природе, результат часто сложно изготовить. По этой причине результат, получаемый в результате оптимизации топологии, часто корректируется с учетом технологичности. Добавление ограничений в рецептуру с целью повышения технологичности является активной областью исследований. В некоторых случаях результаты оптимизации топологии могут быть получены напрямую с использованием аддитивного производства ; Таким образом, оптимизация топологии является ключевой частью проектирования аддитивного производства .

Постановка задачи

Задачу оптимизации топологии можно записать в общей форме задачи оптимизации следующим образом:

{\begin{aligned}&{\underset {\rho }{\operatorname {minimize} }}&&F=F(\mathbf {u(\rho ),\rho } )=\int _{\Omega }f(\mathbf {u(\rho ),\rho } )\mathrm {d} V\\&\operatorname {subject\;to} &&G_{0}(\rho )=\int _{\Omega }\rho \mathrm {d} V-V_{0}\leq 0\\&&&G_{j}(\mathbf {u} (\rho ),\rho )\leq 0{\text{ with }}j=1,...,m\end{aligned}}

Постановка задачи включает в себя следующее:

Целевая функция $F(\mathbf {u(\rho ),\rho } )$ . Эта функция представляет количество, которое минимизируется для достижения наилучшей производительности. Наиболее распространенной целевой функцией является податливость, при которой минимизация податливости приводит к максимизации жесткости конструкции.
Распределение материала как переменная задачи. Это описывается плотностью материала в каждом месте. $\rho (\mathbf {x} )$ . Материал либо присутствует (обозначается 1), либо отсутствует (обозначается 0). $\mathbf {u} =\mathbf {u} (\mathbf {\rho } )$ поле состояния, которое удовлетворяет линейному или нелинейному уравнению состояния в зависимости от $\rho$ .
Дизайнерское пространство $(\Omega )$ . Это указывает на допустимый объем, в пределах которого может существовать конструкция. Требования к сборке и упаковке, доступность людей и инструментов — вот некоторые из факторов, которые необходимо учитывать при определении этого пространства. При определении пространства проектирования области или компоненты модели, которые не могут быть изменены в ходе оптимизации, считаются непроектными областями.
$\scriptstyle m$ ограничения $G_{j}(\mathbf {u} (\rho ),\rho )\leq 0$ характеристика, которой должно удовлетворять решение. Примерами являются максимальное количество распределяемого материала (ограничение объема) или максимальные значения напряжения.

Оценка $\mathbf {u(\rho )}$ часто включает в себя решение дифференциального уравнения. Чаще всего это делается с использованием метода конечных элементов , поскольку эти уравнения не имеют известного аналитического решения.

Методологии внедрения

Существуют различные методологии реализации, которые использовались для решения задач оптимизации топологии.

Решение с дискретными/бинарными переменными

Решение задач оптимизации топологии в дискретном смысле осуществляется путем дискретизации области проектирования на конечные элементы. Плотность материала внутри этих элементов затем рассматривается как переменная задачи. В этом случае плотность материала, равная единице, указывает на наличие материала, а ноль указывает на отсутствие материала. Поскольку достижимая топологическая сложность конструкции зависит от количества элементов, большое их количество является предпочтительным. Большое количество конечных элементов увеличивает достижимую топологическую сложность, но имеет свою цену. Во-первых, решение системы МКЭ становится дороже. Во-вторых, недоступны алгоритмы, способные обрабатывать большое количество (нередко несколько тысяч элементов) дискретных переменных с множеством ограничений. Более того, они практически нечувствительны к изменениям параметров. ^[1] В литературе сообщалось о проблемах с числом переменных до 30 000. ^[2]

Решение задачи с непрерывными переменными

Ранее заявленные сложности с решением задач оптимизации топологии с использованием двоичных переменных заставили сообщество искать другие варианты. Одним из них является моделирование плотностей с непрерывными переменными. Плотность материала теперь также может достигать значений от нуля до единицы. Доступны алгоритмы на основе градиента, которые обрабатывают большое количество непрерывных переменных и множество ограничений. Но свойства материала необходимо моделировать в непрерывном режиме. Это делается посредством интерполяции. Одной из наиболее применяемых методологий интерполяции является метод твердого изотропного материала с пенализацией (SIMP). ^[3]^[4] Эта интерполяция по сути является степенным законом. $E\;=\;E_{0}\,+\,\rho ^{p}(E_{1}-E_{0})$ . Он интерполирует модуль Юнга материала в скалярное поле выбора. Значение параметра штрафа $p$ обычно принимается между $[1,\,3]$ . Было показано, что это подтверждает микроструктуру материалов. ^[5] В методе SIMP добавляется нижняя граница модуля Юнга: $E_{0}$ , чтобы убедиться, что производные целевой функции не равны нулю, когда плотность становится равной нулю. Чем выше коэффициент штрафа, тем больше SIMP наказывает алгоритм за использование недвоичных плотностей. К сожалению, параметр штрафа также вносит невыпуклости. ^[6]

Коммерческое программное обеспечение

На рынке существует несколько коммерческих программ по оптимизации топологии. Большинство из них используют оптимизацию топологии как подсказку, как должна выглядеть оптимальная конструкция, и требуется ручное восстановление геометрии. Существует несколько решений, позволяющих создавать оптимальные конструкции, готовые для аддитивного производства.

Примеры

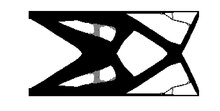
Структурное соответствие

Жесткая конструкция — это конструкция, которая имеет минимально возможное смещение при заданном наборе граничных условий. Глобальной мерой смещений является энергия деформации (также называемая податливостью ) конструкции при заданных граничных условиях. Чем меньше энергия деформации, тем выше жесткость конструкции. Итак, целевая функция задачи – минимизация энергии деформации.

В широком смысле можно представить, что чем больше материала, тем меньше прогиб, поскольку будет больше материала, способного противостоять нагрузкам. Итак, оптимизация требует противоположного ограничения — ограничения объема. На самом деле это фактор стоимости, так как мы не хотели бы тратить много денег на материал. Чтобы получить общее количество используемого материала, можно выполнить интеграцию поля выбора по объему.

Наконец, для получения окончательной постановки задачи подключаются эластичности, определяющие дифференциальные уравнения.

\min _{\rho }\;\int _{\Omega }{\frac {1}{2}}\mathbf {\sigma } :\mathbf {\varepsilon } \,\mathrm {d} \Omega

подлежит:

$\rho \,\in \,[0,\,1]$
$\int _{\Omega }\rho \,\mathrm {d} \Omega \;\leq \;V^{*}$
$\mathbf {\nabla } \cdot \mathbf {\sigma } \,+\,\mathbf {F} \;=\;{\mathbf {0} }$
$\mathbf {\sigma } \;=\;{\mathsf {C}}:\mathbf {\varepsilon }$

Но прямая реализация такой задачи в рамках конечных элементов по-прежнему невозможна из-за таких проблем, как:

Зависимость сетки. Зависимость сетки означает, что конструкция, полученная на одной сетке, отличается от той, которая будет получена на другой сетке. Особенности дизайна становятся более сложными по мере уточнения сетки. ^[7]
Численные нестабильности — выбор региона в виде шахматной доски. ^[8]

Некоторые методы, такие как фильтрация на основе обработки изображений. ^[9] в настоящее время используются для решения некоторых из этих проблем. Хотя долгое время казалось, что это был чисто эвристический подход, теоретические связи с нелокальной эластичностью были сделаны для подтверждения физического смысла этих методов. ^[10]

Мультифизические задачи

Взаимодействие жидкости и структуры

Взаимодействие жидкости со структурой — это сильно связанное явление, касающееся взаимодействия неподвижной или движущейся жидкости и упругой структуры. Многие инженерные приложения и природные явления подвержены взаимодействию жидкости со структурой, и поэтому учет таких эффектов имеет решающее значение при проектировании многих инженерных приложений. Оптимизация топологии для задач взаимодействия жидких структур изучалась, например, в ссылках. ^[11]^[12]^[13] и. ^[14] Ниже показаны расчетные решения, решенные для различных чисел Рейнольдса. Проектные решения зависят от потока жидкости и указывают на то, что связь между жидкостью и конструкцией решена в задачах проектирования.

Расчетное решение и поле скоростей для Re=1

Расчетное решение и поле скоростей для Re=5

Расчетное решение и поле давления для Re=10

Расчетное решение и поле давления для Re=40

Расчетные решения для различных чисел Рейнольдса для стенки, вставленной в канал с движущейся жидкостью.

Набросок известной задачи о стене. Целью задачи проектирования является минимизация структурного соответствия.

Эволюция проектирования задачи взаимодействия жидкости и конструкции на основе эталона. ^[14] Целью задачи проектирования является минимизация структурного соответствия. Проблема взаимодействия жидкости со структурой моделируется с помощью уравнений Навье-Коши и Навье-Стокса.

Термоэлектрическое преобразование энергии

Набросок проектной задачи. Целью задачи проектирования является пространственное распределение двух материалов, материала A и материала B, чтобы максимизировать такие показатели производительности, как мощность охлаждения или выходная электрическая мощность.

Эволюция конструкции недиагонального термоэлектрического генератора. Проектное решение задачи оптимизации выработки электроэнергии. Производительность устройства была оптимизирована за счет распределения скуттерудита (желтого) и теллурида висмута (синего) с использованием методологии оптимизации топологии на основе плотности. Целью задачи оптимизации является максимизация выходной электрической мощности термоэлектрического генератора.

Эволюция конструкции термоэлектрического охладителя. Целью проектной задачи является максимизация охлаждающей способности термоэлектрического охладителя.

Термоэлектричество — это мультифизическая проблема, которая касается взаимодействия и связи между электрической и тепловой энергией в полупроводниковых материалах. Термоэлектрическое преобразование энергии можно описать двумя отдельно выделенными эффектами: эффектом Зеебека и эффектом Пельтье. Эффект Зеебека касается преобразования тепловой энергии в электрическую, а эффект Пельтье касается преобразования электрической энергии в тепловую. ^[15] Пространственно распределяя два термоэлектрических материала в двумерном пространстве проектирования с помощью методологии оптимизации топологии, ^[16] возможно превышение характеристик составляющих термоэлектрических материалов для термоэлектрических охладителей и термоэлектрических генераторов . ^[17]

3F3D Form Follows Force 3D Printing

Нынешнее распространение технологий 3D-принтеров позволило дизайнерам и инженерам использовать методы оптимизации топологии при разработке новых продуктов. Оптимизация топологии в сочетании с 3D-печатью может привести к уменьшению веса, улучшению структурных характеристик и сокращению цикла от проектирования до производства. Поскольку конструкции, хотя и эффективны, могут быть невозможно реализовать с помощью более традиционных технологий производства. ^{[ нужна ссылка ]}

Внутренний контакт

Внутренний контакт можно включить в оптимизацию топологии, применив третий метод контакта со средой . ^[18]^[19]^[20] Третий метод контакта со средой (TMC) представляет собой неявную контактную формулировку, которая является непрерывной и дифференцируемой. Это делает TMC подходящим для использования с градиентными подходами к оптимизации топологии.

Ссылки

^ Зигмунд, Оле; Мауте, Курт (2013). «Подходы к оптимизации топологии». Структурная и междисциплинарная оптимизация . 48 (6): 1031–1055. дои : 10.1007/s00158-013-0978-6 . S2CID 124426387 .
^ Беккерс, М. (1999). «Оптимизация топологии двойным методом с дискретными переменными» (PDF) . Структурная оптимизация . 17 :14–24. дои : 10.1007/BF01197709 . S2CID 122845784 .
^ Бендсё, член парламента (1989). «Оптимальное проектирование формы как проблема распределения материала». Структурная оптимизация . 1 (4): 193–202. дои : 10.1007/BF01650949 . S2CID 18253872 .
^ [1] , монография по этой теме.
^ Бендсё, член парламента; Зигмунд, О. (1999). «Схемы интерполяции материала в оптимизации топологии» (PDF) . Архив прикладной механики . 69 (9–10): 635–654. Бибкод : 1999AAM....69..635B . дои : 10.1007/s004190050248 . S2CID 11368603 .
^ ван Дейк, НП. Лангелаар, М. ван Кеулен, Ф. Критическое исследование параметризации конструкции при оптимизации топологии; Влияние проектной параметризации на локальные минимумы . . 2-я Международная конференция по инженерной оптимизации, 2010 г.
^ Алер, Грегуар; Анро, Антуан (май 2001 г.). «О некоторых последних достижениях в оптимизации формы» . Известия Академии наук . Серия IIB - Механика. 329 (5). Эльзевир: 383–396. Бибкод : 2001CRASB.329..383A . дои : 10.1016/S1620-7742(01)01349-6 . ISSN 1620-7742 . Проверено 12 сентября 2021 г.
^ Шукла, Авинаш; Мисра, Анади; Кумар, Сунил (сентябрь 2013 г.). «Задача шахматной доски в оптимизации топологии на основе конечных элементов» . Международный журнал достижений в области техники и технологий . 6 (4). CiteSeer: 1769–1774. CiteSeerX 10.1.1.670.6771 . ISSN 2231-1963 . Проверено 14 февраля 2022 г.
^ Бурден, Блез (30 марта 2001 г.). «Фильтры в оптимизации топологии» . Международный журнал численных методов в технике . 50 (9). Уайли: 2143–2158. Бибкод : 2001IJNME..50.2143B . дои : 10.1002/nme.116 . ISSN 1097-0207 . S2CID 38860291 . Проверено 2 августа 2020 г.
^ Зигмунд, Оле; Мауте, Курт (октябрь 2012 г.). «Фильтрация чувствительности с точки зрения механики сплошных сред» . Структурная и междисциплинарная оптимизация . 46 (4). Спрингер: 471–475. дои : 10.1007/s00158-012-0814-4 . ISSN 1615-1488 . S2CID 253680268 . Проверено 17 июня 2021 г.
^ Юн, Гиль Хо (2010). «Оптимизация топологии стационарных задач взаимодействия жидкости и конструкции с использованием новой монолитной формулировки». Международный журнал численных методов в технике . 82 (5): 591–616. Бибкод : 2010IJNME..82..591Y . дои : 10.1002/nme.2777 . S2CID 122993997 .
^ Пичелли, Р.; Висенте, ВМ; Паванелло, Р. (2017). «Эволюционная оптимизация топологии для минимизации структурного соответствия с учетом нагрузок FSI, зависящих от конструкции». Конечные элементы в анализе и проектировании . 135 : 44–55. дои : 10.1016/j.finel.2017.07.005 .
^ Дженкинс, Николас; Мауте, Курт (2016). «Подход с погруженными границами для оптимизации формы и топологии стационарных задач взаимодействия жидкости и конструкции». Структурная и междисциплинарная оптимизация . 54 (5): 1191–1208. дои : 10.1007/s00158-016-1467-5 . S2CID 124632210 .
^ Перейти обратно: ^а ^б Лундгаард, Кристиан; Александерсен, Джо; Чжоу, Миндун; Андреасен, Каспер Шусбо; Зигмунд, Оле (2018). «Возврат к оптимизации топологии на основе плотности для задач взаимодействия жидкости и структуры» (PDF) . Структурная и междисциплинарная оптимизация . 58 (3): 969–995. дои : 10.1007/s00158-018-1940-4 . S2CID 125798826 .
^ Роу, Дэвид Майкл. Справочник по термоэлектрике: от макро к нано . ЦРК Пресс, 2005.
^ Лундгаард, Кристиан; Зигмунд, Оле (2018). «Методология оптимизации топологии на основе плотности для решения задач термоэлектрического преобразования энергии» (PDF) . Структурная и междисциплинарная оптимизация . 57 (4): 1427–1442. дои : 10.1007/s00158-018-1919-1 . S2CID 126031362 .
^ Лундгаард, Кристиан; Зигмунд, Оле; Бьорк, Расмус (2018). «Оптимизация топологии сегментированных термоэлектрических генераторов» . Журнал электронных материалов . 47 (12): 6959–6971. Бибкод : 2018JEMat..47.6959L . дои : 10.1007/s11664-018-6606-x . S2CID 105113187 .
^ Перейти обратно: ^а ^б Фредериксен, Андреас Хенрик; Зигмунд, Оле; Пулиос, Константинос (07 октября 2023 г.). «Топологическая оптимизация самоконтактирующих структур» . Вычислительная механика . 73 (4): 967–981. arXiv : 2305.06750 . Бибкод : 2023CompM..73..967F . дои : 10.1007/s00466-023-02396-7 . ISSN 1432-0924 .
^ Блюм, Гор Лукас; Зигмунд, Оле; Пулиос, Константинос (04 марта 2021 г.). «Моделирование внутреннего контакта для оптимизации топологии конечной деформации» . Вычислительная механика . 67 (4): 1099–1114. arXiv : 2010.14277 . Бибкод : 2021CompM..67.1099B . дои : 10.1007/s00466-021-01974-x . ISSN 0178-7675 . S2CID 225076340 .
^ Риггерс, П.; Шредер, Дж.; Шварц, А. (30 марта 2013 г.). «Метод конечных элементов для контакта с использованием третьей среды» . Вычислительная механика . 52 (4): 837–847. Бибкод : 2013CompM..52..837W . дои : 10.1007/s00466-013-0848-5 . ISSN 0178-7675 . S2CID 254032357 .

Дальнейшее чтение

Педерсен, Клаус Б.В.; Аллинджер, Питер (2006). «Промышленная реализация и применение оптимизации топологии и будущие потребности». Симпозиум IUTAM по оптимизации топологического проектирования конструкций, машин и материалов . Механика твердого тела и ее приложения. Том. 137. Спрингер. стр. 229–238. дои : 10.1007/1-4020-4752-5_23 . ISBN 978-1-4020-4729-9 .
Шрамм, Уве; Чжоу, Мин (2006). «Последние разработки в области коммерческой реализации оптимизации топологии». Симпозиум IUTAM по оптимизации топологического проектирования конструкций, машин и материалов . Механика твердого тела и ее приложения. Том. 137. Спрингер. стр. 239–248. дои : 10.1007/1-4020-4752-5_24 . ISBN 978-1-4020-4729-9 .
Махдави, А.; Баладжи, Р.; Фрекер, М.; Мокенштурм, Э.М. (2006). «Оптимизация топологии двумерных континуумов для минимального соответствия с использованием параллельных вычислений». Структурная и междисциплинарная оптимизация . 32 (2): 121–132. дои : 10.1007/s00158-006-0006-1 . S2CID 61564700 .
Лейва, Хуан; Уотсон, Брайан; Косака, Ику (1999). «Современные концепции структурной оптимизации, применяемые к оптимизации топологии». 40-я конференция и выставка «Структуры, структурная динамика и материалы» . Американский институт аэронавтики и астронавтики. дои : 10.2514/6.1999-1388 .

Внешние ссылки

Анимация оптимизации топологии

[1] Зигмунд, Оле; Мауте, Курт (2013). «Подходы к оптимизации топологии». Структурная и междисциплинарная оптимизация . 48 (6): 1031–1055. дои : 10.1007/s00158-013-0978-6 . S2CID 124426387 .

[2] Беккерс, М. (1999). «Оптимизация топологии двойным методом с дискретными переменными» (PDF) . Структурная оптимизация . 17 :14–24. дои : 10.1007/BF01197709 . S2CID 122845784 .

[3] Бендсё, член парламента (1989). «Оптимальное проектирование формы как проблема распределения материала». Структурная оптимизация . 1 (4): 193–202. дои : 10.1007/BF01650949 . S2CID 18253872 .

[book-4] [1] , монография по этой теме.

[5] Бендсё, член парламента; Зигмунд, О. (1999). «Схемы интерполяции материала в оптимизации топологии» (PDF) . Архив прикладной механики . 69 (9–10): 635–654. Бибкод : 1999AAM....69..635B . дои : 10.1007/s004190050248 . S2CID 11368603 .

[6] ван Дейк, НП. Лангелаар, М. ван Кеулен, Ф. Критическое исследование параметризации конструкции при оптимизации топологии; Влияние проектной параметризации на локальные минимумы . . 2-я Международная конференция по инженерной оптимизации, 2010 г.

[7] Алер, Грегуар; Анро, Антуан (май 2001 г.). «О некоторых последних достижениях в оптимизации формы» . Известия Академии наук . Серия IIB - Механика. 329 (5). Эльзевир: 383–396. Бибкод : 2001CRASB.329..383A . дои : 10.1016/S1620-7742(01)01349-6 . ISSN 1620-7742 . Проверено 12 сентября 2021 г.

[8] Шукла, Авинаш; Мисра, Анади; Кумар, Сунил (сентябрь 2013 г.). «Задача шахматной доски в оптимизации топологии на основе конечных элементов» . Международный журнал достижений в области техники и технологий . 6 (4). CiteSeer: 1769–1774. CiteSeerX 10.1.1.670.6771 . ISSN 2231-1963 . Проверено 14 февраля 2022 г.

[9] Бурден, Блез (30 марта 2001 г.). «Фильтры в оптимизации топологии» . Международный журнал численных методов в технике . 50 (9). Уайли: 2143–2158. Бибкод : 2001IJNME..50.2143B . дои : 10.1002/nme.116 . ISSN 1097-0207 . S2CID 38860291 . Проверено 2 августа 2020 г.

[10] Зигмунд, Оле; Мауте, Курт (октябрь 2012 г.). «Фильтрация чувствительности с точки зрения механики сплошных сред» . Структурная и междисциплинарная оптимизация . 46 (4). Спрингер: 471–475. дои : 10.1007/s00158-012-0814-4 . ISSN 1615-1488 . S2CID 253680268 . Проверено 17 июня 2021 г.

[11] Юн, Гиль Хо (2010). «Оптимизация топологии стационарных задач взаимодействия жидкости и конструкции с использованием новой монолитной формулировки». Международный журнал численных методов в технике . 82 (5): 591–616. Бибкод : 2010IJNME..82..591Y . дои : 10.1002/nme.2777 . S2CID 122993997 .

[12] Пичелли, Р.; Висенте, ВМ; Паванелло, Р. (2017). «Эволюционная оптимизация топологии для минимизации структурного соответствия с учетом нагрузок FSI, зависящих от конструкции». Конечные элементы в анализе и проектировании . 135 : 44–55. дои : 10.1016/j.finel.2017.07.005 .

[13] Дженкинс, Николас; Мауте, Курт (2016). «Подход с погруженными границами для оптимизации формы и топологии стационарных задач взаимодействия жидкости и конструкции». Структурная и междисциплинарная оптимизация . 54 (5): 1191–1208. дои : 10.1007/s00158-016-1467-5 . S2CID 124632210 .

[Lundgaard_FSI-14] Перейти обратно: ^а ^б Лундгаард, Кристиан; Александерсен, Джо; Чжоу, Миндун; Андреасен, Каспер Шусбо; Зигмунд, Оле (2018). «Возврат к оптимизации топологии на основе плотности для задач взаимодействия жидкости и структуры» (PDF) . Структурная и междисциплинарная оптимизация . 58 (3): 969–995. дои : 10.1007/s00158-018-1940-4 . S2CID 125798826 .

[15] Роу, Дэвид Майкл. Справочник по термоэлектрике: от макро к нано . ЦРК Пресс, 2005.

[16] Лундгаард, Кристиан; Зигмунд, Оле (2018). «Методология оптимизации топологии на основе плотности для решения задач термоэлектрического преобразования энергии» (PDF) . Структурная и междисциплинарная оптимизация . 57 (4): 1427–1442. дои : 10.1007/s00158-018-1919-1 . S2CID 126031362 .

[17] Лундгаард, Кристиан; Зигмунд, Оле; Бьорк, Расмус (2018). «Оптимизация топологии сегментированных термоэлектрических генераторов» . Журнал электронных материалов . 47 (12): 6959–6971. Бибкод : 2018JEMat..47.6959L . дои : 10.1007/s11664-018-6606-x . S2CID 105113187 .

[:0-18] Перейти обратно: ^а ^б Фредериксен, Андреас Хенрик; Зигмунд, Оле; Пулиос, Константинос (07 октября 2023 г.). «Топологическая оптимизация самоконтактирующих структур» . Вычислительная механика . 73 (4): 967–981. arXiv : 2305.06750 . Бибкод : 2023CompM..73..967F . дои : 10.1007/s00466-023-02396-7 . ISSN 1432-0924 .

[19] Блюм, Гор Лукас; Зигмунд, Оле; Пулиос, Константинос (04 марта 2021 г.). «Моделирование внутреннего контакта для оптимизации топологии конечной деформации» . Вычислительная механика . 67 (4): 1099–1114. arXiv : 2010.14277 . Бибкод : 2021CompM..67.1099B . дои : 10.1007/s00466-021-01974-x . ISSN 0178-7675 . S2CID 225076340 .

[20] Риггерс, П.; Шредер, Дж.; Шварц, А. (30 марта 2013 г.). «Метод конечных элементов для контакта с использованием третьей среды» . Вычислительная механика . 52 (4): 837–847. Бибкод : 2013CompM..52..837W . дои : 10.1007/s00466-013-0848-5 . ISSN 0178-7675 . S2CID 254032357 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]