Паритетная игра

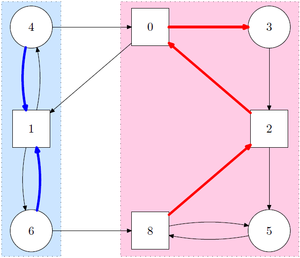
Игра на четность ведется на цветном ориентированном графе , где каждый узел раскрашен в соответствии с приоритетом — одним из (обычно) конечного числа натуральных чисел . Два игрока, 0 и 1, перемещают (одиночный, общий) жетон по краям графа. Владелец узла, на который попадает токен, выбирает узел-преемник (делает следующий ход). Игроки продолжают перемещать жетон, в результате чего образуется (возможно, бесконечный) путь , называемый игрой.

Победителем конечной игры становится игрок, противник которого не может двигаться. Победитель бесконечной игры определяется приоритетами, возникающими в игре. Обычно игрок 0 выигрывает бесконечную игру, если наибольший приоритет, который встречается бесконечно часто в игре, четный. В противном случае игрок 1 выигрывает. Это объясняет слово «паритет» в названии.

Игры на четность лежат на третьем уровне иерархии Бореля и, следовательно, детерминированы . ^[1]

Игры, связанные с играми на четность, неявно использовались в книге Рабина . доказательство разрешимости монадической второго порядка теории n последователей ( S2S для n = 2), где определенность таких игр была доказано. ^[2] Теорема Кнастера – Тарского приводит к относительно простому доказательству детерминированности игр на четность. ^[3]

Более того, игры с паритетом определяются без истории. ^[3]^[4]^[5] Это означает, что если у игрока есть выигрышная стратегия, то у этого игрока есть выигрышная стратегия, которая зависит только от текущей позиции на доске, а не от истории игры.

Решение игры [ править ]

Нерешенная задача в информатике :

Можно ли решить игры на четность за полиномиальное время?

(еще нерешенные проблемы по информатике)

Решение игры на четность, играемой на конечном графе, означает решение для данной начальной позиции, какой из двух игроков имеет выигрышную стратегию. Показано, что эта проблема есть в NP и co-NP , точнее UP и co-UP, ^[6] а также в QP ( квазиполиномиальное время ). ^[7] Остается открытым вопрос, разрешима ли эта проблема принятия решений в PTime .

Учитывая, что игры на четность определяются без истории, решение данной игры на четность эквивалентно решению следующей простой на вид задачи теории графов. Дан конечный цветной ориентированный двудольный граф с n вершинами. $V=V_{0}\cup V_{1}$ , а V окрашены в цвета от 1 до m , существует ли функция выбора, выбирающая одно выходящее ребро из каждой вершины $V_{0}$ , так что результирующий подграф обладает тем свойством, что в каждом цикле наибольший встречающийся цвет является четным.

алгоритм решения игр четность Рекурсивный на

Зелонка изложил рекурсивный алгоритм, который решает игры на четность. Позволять $G=(V,V_{0},V_{1},E,\Omega )$ быть паритетной игрой, где $V_{0}$ соотв. $V_{1}$ являются наборами узлов, принадлежащих игроку 0 соответственно. 1, $V=V_{0}\cup V_{1}$ это набор всех узлов, $E\subseteq V\times V$ - полный набор ребер, и $\Omega :V\rightarrow \mathbb {N}$ — функция назначения приоритета.

Алгоритм Зеленки основан на обозначениях аттракторов. Позволять $U\subseteq V$ быть набором узлов и $i=0,1$ быть игроком. U $i$ -аттрактор $—$ это наименьшее множество узлов $Attr_{i}(U)$ содержащий $U$ , так что $я$ могу принудительно посетить $U$ из каждого узла в $Attr_{i}(U)$ . Его можно определить путем вычисления фиксированной точки:

{\begin{aligned}Attr_{i}(U)^{0}&:=U\\Attr_{i}(U)^{j+1}&:=Attr_{i}(U)^{j}\cup \{v\in V_{i}\mid \exists (v,w)\in E:w\in Attr_{i}(U)^{j}\}\cup \{v\in V_{1-i}\mid \forall (v,w)\in E:w\in Attr_{i}(U)^{j}\}\\Attr_{i}(U)&:=\bigcup _{j=0}^{\infty }Attr_{i}(U)^{j}\end{aligned}}

Другими словами, мы начинаем с начального $U.$ набора Тогда для каждого шага ( $Attr_{i}(U)^{j+1}$ ) добавляются все узлы, принадлежащие игроку 0, которые могут достичь предыдущего набора ( $Attr_{i}(U)^{j}$ ) с единственным ребром и всеми узлами, принадлежащими игроку 1, которые должны достичь предыдущего набора ( $Attr_{i}(U)^{j}$ ) независимо от того, какое преимущество получит игрок 1.

Алгоритм Зеленки основан на рекурсивном спуске по числу приоритетов. Если максимальный приоритет равен 0, сразу видно, что игрок 0 выигрывает всю игру (с произвольной стратегией). В противном случае, пусть $p$ — наибольшее значение и пусть $i=p{\bmod {2}}$ быть игроком, связанным с приоритетом. Позволять $U=\{v\mid \Omega (v)=p\}$ — набор узлов с приоритетом $p$ и пусть $A=Attr_{i}(U)$ быть соответствующим аттрактором игрока $i$ . Игрок $i$ теперь может гарантировать, что каждая игра, которая посещает $A$ бесконечно часто, будет выиграна игроком $i$ .

Рассмотрим игру $G'=G\setminus A$ в котором все узлы и затронутые ребра $A$ удалены. Теперь мы можем решить меньшую игру $G'$ рекурсией и получить пару выигрышных наборов $W'_{i},W'_{1-i}$ . Если $W'_{1-i}$ пусто, то и так $W_{1-i}$ для игры $G$ , поскольку игрок $1-i$ может только решить сбежать из $W_{i}'$ до $A$ , что также приводит к победе игрока $i$ .

В противном случае, если $W'_{1-i}$ не пусто, мы только знаем наверняка, что игрок $1-i$ может выиграть на $W'_{1-i}$ как игрок, $я$ не могу убежать от $W'_{1-i}$ к $A$ (поскольку $A$ является $i$ -аттрактором). Поэтому мы вычисляем аттрактор $B=Attr_{1-i}(W'_{1-i})$ и удалите его из $G,$ чтобы получить меньшую игру $G''=G\setminus B$ . Мы снова решаем ее рекурсией и получаем пару выигрышных наборов. $W''_{i},W''_{1-i}$ . Отсюда следует, что $W_{i}=W''_{i}$ и $W_{1-i}=W''_{1-i}\cup B$ .

В простом псевдокоде алгоритм можно выразить так:

function  $solve(G)$ 
     $p$  := maximal priority in  $G$ 
    if  $p=0$ 
        return  $W_{0},W_{1}:=V,\{\}$ 
    else
         $U$  := nodes in  $G$  with priority  $p$ 
         $i:=p{\bmod {2}}$ 
         $A:=Attr_{i}(U)$ 
         $W_{0}',W_{1}':=solve(G\setminus A)$ 
        if  $W_{1-i}'=\{\}$ 
            return  $W_{i},W_{1-i}:=V,\{\}$ 
         $B:=Attr_{1-i}(W_{1-i}')$ 
         $W_{0}'',W_{1}'':=solve(G\setminus B)$ 
        return  $W_{i},W_{1-i}:=W_{i}'',W_{1-i}''\cup B$

Связанные игры и проблемы их решения [ править ]

Небольшая модификация описанной выше игры и связанной с ней проблемы теории графов делает решение игры NP-трудным . Модифицированная игра имеет условие приемки Рабина . В частности, в приведенном выше сценарии двудольного графа проблема состоит в том, чтобы определить, существуют ли — это функция выбора, выбирающая одно выходящее ребро из каждой вершины V ₀ , так что результирующий подграф обладает свойством, что в каждом цикле (и, следовательно, в каждом сильно связном компоненте ) существует случай, когда существуют i и узел с цветом 2 i и без узла с цветом 2 i + 1...

Обратите внимание, что в отличие от игр на четность, эта игра больше не симметрична относительно игроков 0 и 1.

с логикой и автоматов Связь теорией

Несмотря на свой интересный статус с точки зрения теории сложности, решение игр на четность можно рассматривать как алгоритмическую основу для решения задач автоматической проверки и синтеза контроллера. для задача проверки модели модального μ-исчисления Например, известно, что эквивалентна решению игры на четность. Кроме того, проблемы принятия решений, такие как достоверность или выполнимость модальной логики, могут быть сведены к решению игры на четность.

Ссылки [ править ]

^ Д. А. Мартин : Определенность Бореля, Анналы математики, том 102, № 2, стр. 363–371 (1975)
^ Рабин, Миссури (1969). «Разрешимость теорий и автоматов второго порядка на бесконечных деревьях» . Труды Американского математического общества . 141 . Американское математическое общество: 1–35. дои : 10.2307/1995086 . JSTOR 1995086 .
^ Jump up to: Перейти обратно: ^а ^б Э.А. Эмерсон и К.С. Ютла: Древовидные автоматы, мю-исчисление и детерминированность, IEEE Proc. Основы информатики, стр. 368–377 (1991), ISBN 0-8186-2445-0
^ А. Мостовский: Игры с запрещенными позициями, Гданьский университет, Техн. Отчет 78 (1991 г.)
^ Зеленка, Вт (1998). «Бесконечные игры на конечно раскрашенных графах с приложениями к автоматам на бесконечных деревьях» . Теор. Вычислить. Наука . 200 (1–2): 135–183. дои : 10.1016/S0304-3975(98)00009-7 .
^ Марцин Юрдзински (1998), «Определение победителя в играх на паритет происходит в UP∩ co-UP» (PDF) , Information Processing Letters , 68 (3), Elsevier: 119–124, doi : 10.1016/S0020-0190(98) 00150-1
^ Калуде, Кристиан С; Джайн, Санджай; Хусаинов, Бахадыр; Ли, Вэй; Стефан, Франк, «Определение игр на четность за квазиполиномиальное время» (PDF) , Stoc, 2017 г.

Эрих Гредель, Фокион Г. Колайтис, Леонид Либкин , Маартен Маркс, Джоэл Спенсер , Моше Ю. Варди , Иде Венема, Скотт Вайнштейн (2007). Теория конечных моделей и ее приложения . Спрингер. ISBN 978-3-540-00428-8 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

Дальнейшее чтение [ править ]

Э. Гредель, В. Томас, Т. Вилке (ред.): Автоматы, логика и бесконечные игры , Springer LNCS 2500 (2003), ISBN 3-540-00388-6
В. Зелонка: Бесконечные игры на конечно цветных графах с приложениями к автоматам на бесконечном дереве , TCS, 200(1-2):135-183, 1998

Внешние ссылки [ править ]

Два современных набора инструментов для решения игр на четность:

[1] Д. А. Мартин : Определенность Бореля, Анналы математики, том 102, № 2, стр. 363–371 (1975)

[2] Рабин, Миссури (1969). «Разрешимость теорий и автоматов второго порядка на бесконечных деревьях» . Труды Американского математического общества . 141 . Американское математическое общество: 1–35. дои : 10.2307/1995086 . JSTOR 1995086 .

[EJ-3] Jump up to: Перейти обратно: ^а ^б Э.А. Эмерсон и К.С. Ютла: Древовидные автоматы, мю-исчисление и детерминированность, IEEE Proc. Основы информатики, стр. 368–377 (1991), ISBN 0-8186-2445-0

[4] А. Мостовский: Игры с запрещенными позициями, Гданьский университет, Техн. Отчет 78 (1991 г.)

[ZL-5] Зеленка, Вт (1998). «Бесконечные игры на конечно раскрашенных графах с приложениями к автоматам на бесконечных деревьях» . Теор. Вычислить. Наука . 200 (1–2): 135–183. дои : 10.1016/S0304-3975(98)00009-7 .

[6] Марцин Юрдзински (1998), «Определение победителя в играх на паритет происходит в UP∩ co-UP» (PDF) , Information Processing Letters , 68 (3), Elsevier: 119–124, doi : 10.1016/S0020-0190(98) 00150-1

[7] Калуде, Кристиан С; Джайн, Санджай; Хусаинов, Бахадыр; Ли, Вэй; Стефан, Франк, «Определение игр на четность за квазиполиномиальное время» (PDF) , Stoc, 2017 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]