Слияние (абстрактное переписывание)

Рис.1: Название «слияние» заимствовано из географии и означает место встречи двух водоемов.

В информатике и математике слияние — это свойство переписывания систем, описывающее, какие термины в такой системе можно переписать более чем одним способом, чтобы получить один и тот же результат. В этой статье описываются свойства абстрактной системы переписывания в наиболее абстрактной ситуации .

Мотивирующие примеры

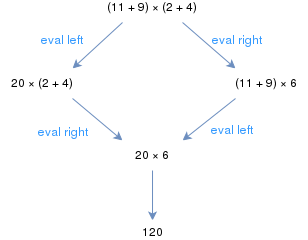
Обычные правила элементарной арифметики образуют абстрактную систему переписывания.Например, выражение (11 + 9) × (2 + 4) можно вычислять, начиная с левой или с правой скобки;однако в обоих случаях в конечном итоге получается один и тот же результат.Если каждое арифметическое выражение дает один и тот же результат независимо от стратегии сокращения, то система арифметической переписывания называется сливающейся по основанию. Системы арифметической переписывания могут быть сливающимися или только слитными по основанию, в зависимости от деталей системы переписывания.

Второй, более абстрактный пример получается из следующего доказательства того, что каждый группы элемент равен обратному своему обратному:

Групповые аксиомы

А1	1 ⋅ а	= а
А2	а −1 ⋅ а	= 1
А3	( а ⋅ б ) ⋅ в	знак равно а ⋅ ( б ⋅ c )

Доказательство R4 : a ⁻¹ ⋅( а ⋅ б ) знак равно б

	а −1 ⋅ ( а ⋅ б )
=	( а −1 ⋅ а ) ⋅ б	по А3(г)
=	1 ⋅ б	по А2
=	б	by A1

Доказательство R6 : ( a ⁻¹ ) ⁻¹ ⋅ 1 = а

	( а −1 ) −1 ⋅ 1
=	( а −1 ) −1 ⋅ ( а −1 ⋅ а )	по A2(r)
=	а	by R4

Доказательство R10 : ( a ⁻¹ ) ⁻¹ ⋅ б = а ⋅ б

	( а −1 ) −1 ⋅ б
=	( а −1 ) −1 ⋅ ( а −1 ⋅ ( а ⋅ б ))	by R4(r)
=	а ⋅ б	by R4

Доказательство R11 : a ⋅ 1 = a

	а ⋅ 1
=	( а −1 ) −1 ⋅ 1	на R10(r)
=	а	по R6

Доказательство R12 : ( a ⁻¹ ) ⁻¹ = а

	( а −1 ) −1
=	( а −1 ) −1 ⋅ 1	по R11(r)
=	а	по R6

Это доказательство начинается с данных аксиом группы A1–A3 и устанавливает пять предложений R4, R6, R10, R11 и R12, каждое из которых использует некоторые более ранние предложения, а R12 является основной теоремой. Некоторые доказательства требуют неочевидных или даже творческих шагов, таких как применение аксиомы А2 в обратном порядке, тем самым переписывая «1» на «а ». ⁻¹ ⋅ a" на первом этапе доказательства R6. Одним из исторических мотивов разработки теории переписывания терминов было избежание необходимости таких шагов, которые трудно найти неопытному человеку, не говоря уже о компьютерной программе. .

Если система переписывания терминов является сливающейся и завершающейся , существует простой метод доказательства равенства между двумя выражениями (также известными как термины ) s и t :Начиная с s , примените равенства слева направо как можно дольше, в конечном итоге получая член s' . получим из t терм t' Аналогичным образом .Если оба термина s' и t' буквально совпадают, то s и t оказываются равными.Что еще более важно, если они не согласны, то s и t не могут быть равными.То есть любые два термина s и t , равенство которых вообще можно доказать, можно сделать с помощью этого метода.

Успех этого метода не зависит от определенного сложного порядка применения правил перезаписи, поскольку слияние гарантирует, что любая последовательность применения правил в конечном итоге приведет к одному и тому же результату (в то время как свойство завершения гарантирует, что любая последовательность в конечном итоге достигнет конца). совсем). можно предоставить сливающуюся и завершающую систему переписывания терминов Следовательно, если для некоторой эквациональной теории , для доказательства равенства терминов не требуется ни капли творчества; следовательно, эта задача становится поддающейся компьютерным программам. Современные подходы используют более общие абстрактные системы переписывания , а не терминов системы переписывания ; последние являются частным случаем первых.

и

Рис.2: На этой диаграмме a сводится к b или c за ноль или более шагов перезаписи (обозначено звездочкой). Чтобы отношение перезаписи было конфлуэнтным, оба редукта, в свою очередь, должны сводиться к некоторому общему d .

Систему перезаписи можно выразить как ориентированный граф , в котором узлы представляют собой выражения, а ребра представляют перезаписи. Так, например, если выражение a можно переписать в b , то мы говорим, что является сокращением a ( b альтернативно, сводится к a или a является расширением b b ). Это представлено с использованием стрелочных обозначений; a → b указывает, что a сводится к b . Интуитивно это означает, что соответствующий граф имеет направленное ребро от a до b .

существует путь Если между двумя узлами графа c и d , то он образует редукционную последовательность . Так, например, если c → c′ → c′′ → ... → d′ → d , то мы можем написать c ∗ → d , указывая на существование последовательности приведения от c к d . Формально ∗ → является рефлексивно-транзитивным замыканием →. Используя пример из предыдущего абзаца, мы имеем (11+9)×(2+4) → 20×(2+4) и 20×(2+4) → 20×6, поэтому (11+9)×( 2+4) ∗ → 20×6.

Установив это, слияние можно определить следующим образом. a ∈ S считается конфлюэнтным , если для всех пар b , c ∈ S таких, что a ∗ → b и a ∗ → c , существует d ∈ S такой, что b ∗ → d и c ∗ → d (обозначается $b\mathbin {\downarrow } c$). Если каждое a ∈ S конфлюэнтно, мы говорим, что → конфлюэнтно. Это свойство также иногда называют свойством ромба по форме диаграммы, показанной справа. Некоторые авторы оставляют термин «свойство алмаза» для варианта диаграммы с единичными редукциями повсюду; то есть всякий раз, когда a → b и a → c , должен существовать d такой, что b → d и c → d . Вариант с одной редукцией строго сильнее, чем вариант с несколькими редукцией.

Слияние земли

Система переписывания терминов является конфлюэнтной по основанию, если каждый основной термин конфлюэнтен, то есть каждый термин без переменных.

Местное слияние

Рис.3: Циклическая, локально-слитная, но не глобально-сливающаяся система перезаписи.

Рис.4: Бесконечная нециклическая, локально-слитная, но не глобально-слитная система перезаписи

Элемент a ∈ S называется локально конфлюэнтным (или слабо конфлюэнтным) . ), если для всех b , c ∈ S с a → b и a → c существует d ∈ S с такими, что b ∗ → d и c ∗ → d . Если каждый a ∈ S локально слит, то → называется локально слитным или обладающим слабым свойством Чёрча–Россера . Это отличается от слияния тем, что b и c должны быть уменьшены из a за один шаг. По аналогии с этим слияние иногда называют глобальным слиянием .

Отношение ∗ → , введенное как обозначение последовательностей редукции, можно рассматривать как самостоятельную систему переписывания, отношением которой является рефлексивно-транзитивное замыкание → . Поскольку последовательность последовательностей редукции снова является последовательностью редукции (или, что то же самое, поскольку формирование рефлексивно-транзитивного замыкания идемпотентно ) , ∗ ∗ → = ∗ → . Отсюда следует, что → конфлюэнтно тогда и только тогда, когда ∗ → локально конфлюэнтно.

Система переписывания может быть локально слитной, но не быть (глобально) слитной. Примеры показаны на рисунках 3 и 4. Однако лемма Ньюмана утверждает, что если локально конфлюэнтная система переписывания не имеет бесконечных последовательностей редукции (в этом случае она называется завершающей или сильно нормализующей ), то она глобально конфлюэнтна.

-

Говорят, что система переписывания обладает свойством Чёрча–Россера тогда и только тогда, когда $x{\stackrel {*}{\leftrightarrow }}y$ подразумевает $x{\mathbin {\downarrow }}y$ для всех объектов x , y . Алонсо Чёрч и Дж. Баркли Россер доказали в 1936 году, что лямбда-исчисление обладает этим свойством; отсюда и название объекта недвижимости. (Тот факт, что лямбда-исчисление обладает этим свойством, также известен как теорема Чёрча-Россера .) В системе переписывания со свойством Чёрча-Россера проблема слов может быть сведена к поиску общего преемника. В системе Чёрча-Россера объект имеет не более одной нормальной формы ; то есть нормальная форма объекта уникальна, если она существует, но вполне может и не существовать. Например, в лямбда-исчислении выражение (λx.xx)(λx.xx) не имеет нормальной формы, поскольку существует бесконечная последовательность β-редукций (λx.xx)(λx.xx) → (λx.xx) (λx.xx) → ...

Система переписывания обладает свойством Чёрча–Россера тогда и только тогда, когда она конфлюэнтна. Из-за этой эквивалентности в литературе встречаются значительные различия в определениях. Например, в «Терезе» свойство Чёрча-Россера и слияние определяются как синонимы и идентичны определению слияния, представленному здесь; Черч-Россер, определенный здесь, остается безымянным, но задается как эквивалентное свойство; этот отход от других текстов является преднамеренным.

Полуслияние

Определение локального слияния отличается от определения глобального слияния тем, что учитываются только элементы, полученные из данного элемента за один шаг перезаписи. Рассматривая один элемент, достигнутый за один шаг, и другой элемент, достигнутый с помощью произвольной последовательности, мы приходим к промежуточному понятию полуконфлюэнтности: a ∈ S называется полуконфлюэнтным, если для всех b , c ∈ S с a → b и a ∗ → c существует d ∈ S такой, что b ∗ → d и c ∗ → d ; если каждое a ∈ S полуконфлюэнтно, мы говорим, что → полуконфлюэнтно.

Полуслитный элемент не обязательно должен быть слитным, но полуслитная система переписывания обязательно слитна, а слитная система тривиально полуслитна.

Сильное слияние

Сильное слияние — это еще один вариант локального слияния, который позволяет нам заключить, что система перезаписи глобально конфлюэнтна. Элемент a ∈ S называется сильно конфлюэнтным , если для всех b , c ∈ S с a → b и a → c существует d ∈ S с таким, что b ∗ → d и либо c → d , либо c = d ; если каждое a ∈ S сильно конфлюэнтно, мы говорим, что → сильно конфлюэнтно.

Сливающийся элемент не обязательно должен быть сильно слитным, но сильно слитная система переписывания обязательно слита.

Примеры конфлюэнтных систем

• Приведение полиномов по модулю идеала представляет собой конфлюэнтную систему переписывания при условии, что кто-то работает с базисом Грёбнера .
• Теорема Мацумото следует из слияния отношений кос.
• β-редукция λ-членов конфликтна по теореме Чёрча – Россера .

См. также

• Сходимость (логика)
• Критическая пара (логика)
• Нормальная форма (абстрактное переписывание)

Ссылки

• «Тереза»; Брум, Марк; Клоп, Ян Виллем ; де Вриер, Роэль (2003). Системы переписывания терминов . Кембриджские трактаты по теоретической информатике. Издательство Кембриджского университета. ISBN  0-521-39115-6 .
• Баадер, Франц ; Нипков, Тобиас (1998). Переписывание терминов и все такое . Издательство Кембриджского университета. ISBN  978-0-521-77920-3 .
• Блазиус, К.Х.; Бюркерт, Х.-Ю., ред. (1992). Системы вычетов . Ольденбург. п. 291.

Внешние ссылки

• Вайсштейн, Эрик В. «Слияние» . Математический мир .