Отношения Рамберга и Осгуда

Уравнение Рамберга-Осгуда было создано для описания нелинейной зависимости между напряжением и деформацией , то есть кривой растяжения-деформации , в материалах вблизи их пределов текучести . Это особенно применимо к металлам, которые затвердевают пластической деформацией (см. Наклейка ), демонстрируя плавный упруго-пластический переход. Поскольку это феноменологическая модель , очень важно проверить ее соответствие фактическим экспериментальным данным для конкретного интересующего материала.

В исходном виде уравнение деформации (деформации) имеет вид

$\varepsilon ={\frac {\sigma }{E}}+K\left({\frac {\sigma }{E}}\right)^{n}$

здесь

$\varepsilon$ это напряжение ,

$\sigma$ это стресс ,

$E$ – модуль Юнга , а

$K$ и $n$ являются константами, зависящими от рассматриваемого материала. В этой форме K и n не совпадают с константами, обычно встречающимися в уравнении Холломона .

Уравнение по существу предполагает часть упругой деформации кривой растяжения-деформации: $\varepsilon _{e}$, можно смоделировать линией, а пластиковую часть, $\varepsilon _{p}$, можно смоделировать с помощью степенного закона. Упругие и пластические компоненты суммируются, чтобы найти общую деформацию.

$\varepsilon =\varepsilon _{e}+\varepsilon _{p}$

Первое слагаемое в правой части, ${\sigma }/{E}\,$, равен упругой части деформации, а второй член $\ K({\sigma }/{E})^{n}$, учитывает пластиковую часть, параметры $K$ и $n$ описывающее при затвердевании поведение материала . Представляя предел текучести материала, $\sigma _{0}$и определение нового параметра, $\alpha$, связанный с $K$ как $\alpha =K({\sigma _{0}}/{E})^{n-1}\,$, удобно переписать термин в крайней правой части следующим образом:

$\ K\left({\frac {\sigma }{E}}\right)^{n}=\alpha {\frac {\sigma }{E}}\left({\frac {\sigma }{\sigma _{0}}}\right)^{n-1}$

Заменив первое выражение, уравнение Рамберга–Осгуда можно записать в виде

$\varepsilon ={\frac {\sigma }{E}}+\alpha {\frac {\sigma }{E}}\left({\frac {\sigma }{\sigma _{0}}}\right)^{n-1}$

Поведение при затвердевании и смещение текучести

В последней форме модели Рамберга – Осгуда поведение материала при упрочнении зависит от констант материала. $\alpha \,$ и $n\,$. Из-за степенной зависимости между напряжением и пластической деформацией модель Рамберга-Осгуда предполагает, что пластическая деформация присутствует даже при очень низких уровнях напряжения. Тем не менее, при малых приложенных напряжениях и при обычно используемых значениях материальных констант $\alpha$ и $n$, пластическая деформация остается незначительной по сравнению с упругой деформацией. С другой стороны, при уровне стресса выше $\sigma _{0}$пластическая деформация становится все больше упругой.

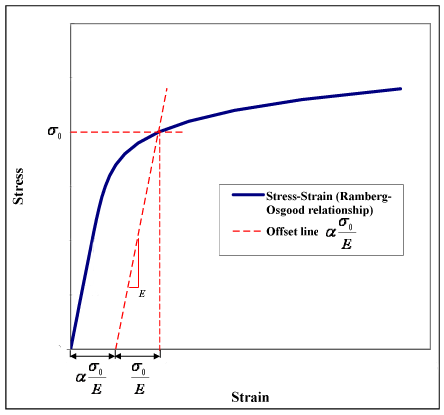
Значение $\alpha {\frac {\sigma _{0}}{E}}$ можно рассматривать как смещение доходности , как показано на рисунке 1. Это происходит из-за того, что $\varepsilon =(1+\alpha ){{\sigma _{0}}/{E}}\,$, когда $\sigma =\sigma _{0}\,$.

Соответственно (см. рисунок 1):

упругая деформация при текучести = ${{\sigma _{0}}/{E}}\,$

пластическая деформация при текучести = $\alpha ({\sigma _{0}}/E)\,$ = смещение доходности

Часто используемые значения для $n\,$ составляют ~5 или больше, хотя более точные значения обычно получают путем подбора экспериментальных данных по растяжению (или сжатию). Значения для $\alpha \,$ также может быть найдена путем подгонки к экспериментальным данным, хотя для некоторых материалов ее можно зафиксировать, чтобы сдвиг текучести был равен принятому значению деформации 0,2 %, что означает:

$\alpha {\frac {\sigma _{0}}{E}}=0.002$

Рисунок 1 : Общее представление кривой растяжения-деформации с помощью уравнения Рамберга-Осгуда. Деформация, соответствующая пределу текучести, представляет собой сумму упругой и пластической составляющих.

Альтернативные составы

Можно найти несколько несколько отличающихся альтернативных формулировок уравнения Рамберга-Осгуда. Поскольку модели являются чисто эмпирическими, часто бывает полезно опробовать разные модели и проверить, какая из них лучше всего подходит к выбранному материалу.

Уравнение Рамберга-Осгуда также можно выразить с помощью параметров Холломона. где $K$ - коэффициент прочности (Па) и $n$ – коэффициент деформационного упрочнения (без единиц измерения).

$\varepsilon ={\frac {\sigma }{E}}+\left({\frac {\sigma }{K}}\right)^{1/n}$

Альтернативно, если предел текучести, $\sigma _{y}$, предполагается при деформации смещения 0,2%, можно вывести следующее соотношение. Обратите внимание, что $n$ снова имеет значение, определенное в исходном уравнении Рамберга-Осгуда, и является обратной величиной коэффициента деформационного упрочнения Холломона .

$\varepsilon ={\frac {\sigma }{E}}+0.002\left({\frac {\sigma }{\sigma _{y}}}\right)^{n}$

См. также

• Вязкопластичность # Модель напряжения течения Джонсона – Кука