Лемма о прокачке для обычных языков

В теории формальных языков лемма о накачке регулярных языков — это лемма , описывающая существенное свойство всех регулярных языков . Неформально оно гласит, что все достаточно длинные строки в обычном языке могут быть перекачаны (то есть иметь среднюю часть строки, повторяемую произвольное количество раз) для создания новой строки, которая также является частью языка. Лемма о накачке полезна для доказательства того, что конкретный язык не является регулярным языком, показывая, что этот язык не обладает этим свойством.

В частности, лемма о накачке утверждает, что для любого регулярного языка $L$ , существует константа $p$ такая, что любая строка $w$ в $L$ длиной не менее $p$ можно разделить на три подстроки $x$ , $y$ и $z$ ( $w=xyz$ , с $y$ непусто), так что строки $xz,xyz,xyyz,xyyyz,...$ также находятся в $L$ . Процесс повторения $y$ ноль или более раз называется «накачкой». Более того, лемма о накачке гарантирует, что длина $xy$ будет максимум $p$ , налагая ограничения на способы, которыми $w$ может быть разделен.

Языки с конечным числом строк не удовлетворяют лемме о накачке, поскольку имеют $p$ равна максимальной длине строки в $L$ плюс один. Таким образом, в $L$ иметь длину больше, чем $p$ .

Лемма о накачке была впервые доказана Майклом Рабином и Даной Скотт в 1959 году. ^[1] и вскоре вновь открыт Иеошуа Бар-Хиллелем , Михой А. Перлесом и Эли Шамиром в 1961 году как упрощение их леммы о накачке для контекстно-свободных языков . ^[2]^[3]

Официальное заявление [ править ]

Позволять $L$ быть обычным языком. Тогда существует целое число $p\geq 1$ в зависимости только от $L$ так, что каждая строка $w$ в $L$ длины как минимум $p$ ( $p$ называется «длиной накачки») ^[4] можно записать как $w=xyz$ (т.е. $w$ можно разделить на три подстроки), удовлетворяющие следующим условиям:

$|y|\geq 1$
$|xy|\leq p$
$(\forall n\geq 0)(xy^{n}z\in L)$

$y$ — это подстрока, которую можно перекачивать (удалять или повторять любое количество раз, при этом результирующая строка всегда находится в $L$ ). (1) означает цикл $y$ для перекачки должна иметь длину хотя бы один, то есть не пустую строку; (2) означает, что цикл должен произойти в течение первого $p$ персонажи. $|x|$ должно быть меньше, чем $p$ (вывод из (1) и (2)), но кроме этого ограничений на $x$ и $z$ .

Проще говоря, для любого обычного языка $L$ , любая достаточно длинная строка $w$ (в $L$ ) можно разделить на 3 части.т.е. $w=xyz$ , такой, что все строки $xy^{n}z$ для $n\geq 0$ также находятся в $L$ .

Ниже приводится формальное выражение леммы о накачке.

${\begin{array}{l}\forall L\subseteq \Sigma ^{*},{\mbox{regular}}(L)\implies \\\quad \exists p\geq 1,\forall w\in L,|w|\geq p\implies \\\qquad \exists x,y,z\in \Sigma ^{*},(w=xyz)\land (|y|\geq 1)\land (|xy|\leq p)\land (\forall n\geq 0,xy^{n}z\in L)\end{array}}$

нерегулярности доказательства леммы для Использование

Лемма о накачке часто используется для доказательства того, что конкретный язык нерегулярен: доказательство от противного может состоять в обнаружении строки (требуемой длины) в языке, лишенной свойства, изложенного в лемме о накачке.

Пример: язык $L=\{a^{n}b^{n}:n\geq 0\}$ над алфавитом $\Sigma =\{a,b\}$ можно показать, что они нерегулярны следующим образом:
Позволять $w,x,y,z$ , и $n$ быть таким, как использовано в формальном утверждении леммы о накачке выше.
Предположим, что некоторая константа $p$ существует, как того требует лемма.
Позволять $w$ в $L$ быть предоставлено $w=a^{p}b^{p}$ , которая представляет собой строку длиннее, чем $p$ .
По лемме о накачке должно существовать разложение $w=xyz$ с $|xy|\leq p$ и $|y|\geq 1$ такой, что $xy^{i}z$ в $L$ для каждого $i\geq 0$ .
С $|xy|\leq p$ , строка $y$ состоит только из экземпляров $a$ .
Потому что $|y|\geq 1$ , он содержит хотя бы один экземпляр буквы $a$ .
Накачка $y$ дать $xy^{2}z$ дает слово с большим количеством экземпляров буквы $a$ чем письмо $b$ , поскольку некоторые случаи $a$ но ни один из $b$ были добавлены.
Поэтому, $xy^{2}z$ не в $L$ что противоречит лемме о накачке.
Поэтому, $L$ не может быть регулярным.

Доказательство того, что язык сбалансированных (т. е. правильно вложенных) круглых скобок не является регулярным, следует той же идее. Данный $p$ , существует строка сбалансированных круглых скобок, которая начинается с более чем $p$ оставленные скобки, так что $y$ будет полностью состоять из левых скобок. Повторяя $y$ , может быть создана строка, содержащая разное количество левых и правых круглых скобок, и поэтому они не могут быть сбалансированы.

леммы о накачке Доказательство

Для каждого регулярного языка существует конечный автомат (FSA), который принимает этот язык. Количество состояний в таком FSA подсчитывается, и это количество используется в качестве длины накачки. $p$ . Для строки длиной не менее $p$ , позволять $q_{0}$ быть начальным состоянием и пусть $q_{1},...,q_{p}$ быть последовательностью следующих $p$ состояния, посещенные при выдаче строки. Поскольку у FSA есть только $p$ состояния, в этой последовательности $p+1$ посещенных состояниях должно быть хотя бы одно повторяющееся состояние. Писать $q_{s}$ для такого государства. Переходы, которые выводят машину из первого состояния $q_{s}$ ко второй встрече государства $q_{s}$ соответствовать некоторой строке. Эта строка называется $y$ в лемме, и поскольку машина найдет строку без $y$ порция или с веревкой $y$ повторяется любое число раз, то условия леммы выполнены.

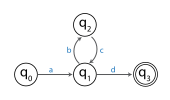
Например, на следующем изображении показан FSA.

FSA принимает строку: abcd . Поскольку эта строка имеет длину, по крайней мере, такую же, как количество состояний, равное четырем (таким образом, общее количество состояний, через которые машина проходит при сканировании abcd, будет равно 5), принцип группировки указывает, что должно быть хотя бы одно состояние. повторяющееся состояние среди начального состояния и следующих четырех посещенных состояний. В этом примере только $q_{1}$ это повторяющееся состояние. Поскольку подстрока bc проводит машину через переходы, начинающиеся с состояния $q_{1}$ и закончить в состоянии $q_{1}$ , эта часть может быть повторена, и FSA все равно примет ее, передав строку abcbcd . В качестве альтернативы часть bc можно удалить, и FSA все равно согласится предоставить строку ad . По лемме о накачке строка abcd разбивается на $x$ порция а , а $y$ часть до н.э. и а $z$ порция д .

В качестве дополнительного замечания: проблема проверки того, может ли данная строка быть принята данным недетерминированным конечным автоматом без повторного посещения какого-либо состояния, является NP-трудной .

Общая версия леммы о прокачке для обычных языков [ править ]

Если язык $L$ регулярно, то существует число $p\geq 1$ (длина накачки) такая, что каждая струна $uwv$ в $L$ с $|w|\geq p$ можно записать в форме

uwv=uxyzv

со струнами $x$ , $y$ и $z$ такой, что $|xy|\leq p$ , $|y|\geq 1$ и

uxy^{i}zv

находится в

L

для каждого целого числа

i\geq 0

. ^[5]

Таким образом, приведенная выше стандартная версия представляет собой особый случай, когда оба $u$ и $v$ пустая строка.

Поскольку общая версия предъявляет к языку более строгие требования, ее можно использовать для доказательства нерегулярности многих других языков.

Неверность обратной леммы [ править ]

Хотя лемма о накачке утверждает, что все регулярные языки удовлетворяют описанным выше условиям, обратное утверждение неверно: язык, удовлетворяющий этим условиям, все равно может быть нерегулярным. Другими словами, как исходная, так и общая версия леммы о накачке дают необходимое , но недостаточное условие регулярности языка.

Например, рассмотрим следующий язык:

{\begin{matrix}L&=&\{uvwxy:u,y\in \{0,1,2,3\}^{*};v,w,x\in \{0,1,2,3\}\land (v=w\lor v=x\lor x=w)\}\\&&\cup \ \{w:w\in \{0,1,2,3\}^{*}\land {\text{precisely }}{\tfrac {1}{7}}{\text{ of the characters in }}w{\text{ are 3's}}\}\end{matrix}}

.

Другими словами, $L$ содержит все строки алфавита $\{0,1,2,3\}$ с подстрокой длиной 3, включающей повторяющийся символ, а также со всеми строками в этом алфавите, в которых ровно 1/7 символов строки составляют тройки. Этот язык не является штатным, но его все равно можно «прокачать» с помощью $p=5$ . Предположим, длина некоторой строки s не менее 5. Тогда, поскольку в алфавите всего четыре символа, по крайней мере два из первых пяти символов в строке должны быть повторяющимися. Они разделены не более чем тремя символами.

Если повторяющиеся символы разделены 0 символами или 1, перекачайте один из двух других символов в строке, что не повлияет на подстроку, содержащую дубликаты.
Если повторяющиеся символы разделены 2 или 3 символами, прокачайте 2 символа, разделяющих их. Перекачка вниз или вверх приводит к созданию подстроки размером 3, содержащей 2 повторяющихся символа.
Второе условие $L$ гарантирует, что $L$ не является регулярным: рассмотрим строку $(013)^{3m}(012)^{i}$ . Эта строка находится в $L$ именно когда $i=4m$ и таким образом $L$ не является регулярным по теореме Майхилла-Нерода .

Теорема Майхилла-Нерода представляет собой тест, который точно характеризует регулярные языки. Типичным методом доказательства регулярности языка является построение либо конечного автомата , либо регулярного выражения для языка.

См. также [ править ]

Примечания [ править ]

^ Рабин, Майкл ; Скотт, Дана (апрель 1959 г.). «Конечные автоматы и проблемы их решения» (PDF) . Журнал исследований и разработок IBM . 3 (2): 114–125. дои : 10.1147/рд.32.0114 . Архивировано из оригинала 14 декабря 2010 года. {{cite journal}}:CS1 maint: unfit URL ( ссылка ) Здесь: Лемма 8, стр.119
^ Бар-Хилель, Ю .; Перлз, М.; Шамир, Э. (1961), «О формальных свойствах грамматик простой фразовой структуры», Журнал фонетики, лингвистики и коммуникационных исследований , 14 (2): 143–172.
^ Джон Э. Хопкрофт; Раджив Мотвани; Джеффри Д. Уллман (2003). Введение в теорию автоматов, языки и вычисления . Эддисон Уэсли. Здесь: разд.4.6, стр.166
^ Берстель, Жан; Лауве, Аарон; Ройтенауэр, Кристоф; Салиола, Франко В. (2009). Комбинаторика слов. Слова Кристоффеля и повторы в словах . Серия монографий по CRM. Том. 27. Провиденс, Род-Айленд: Американское математическое общество . п. 86. ИСБН 978-0-8218-4480-9 . Артикул 1161.68043 .
^ Савич, Уолтер (1982). Абстрактные машины и грамматики . п. 49 . ISBN 978-0-316-77161-0 .

Ссылки [ править ]

Лоусон, Марк В. (2004). Конечные автоматы . Чепмен и Холл/CRC. ISBN 978-1-58488-255-8 . Збл 1086.68074 .
Сипсер, Майкл (1997). «1.4: Нерегулярные языки». Введение в теорию вычислений . Издательство ПВС. стр. 77–83 . ISBN 978-0-534-94728-6 . Збл 1169,68300 .
Хопкрофт, Джон Э .; Уллман, Джеффри Д. (1979). Введение в теорию автоматов, языки и вычисления . Ридинг, Массачусетс: Издательство Addison-Wesley. ISBN 978-0-201-02988-8 . Збл 0426.68001 . (См. главу 3.)
Бахадыр Хусаинов; Анил Нероде (6 декабря 2012 г.). Теория автоматов и ее приложения . Springer Science & Business Media. ISBN 978-1-4612-0171-7 .

[1] Рабин, Майкл ; Скотт, Дана (апрель 1959 г.). «Конечные автоматы и проблемы их решения» (PDF) . Журнал исследований и разработок IBM . 3 (2): 114–125. дои : 10.1147/рд.32.0114 . Архивировано из оригинала 14 декабря 2010 года. {{cite journal}}:CS1 maint: unfit URL ( ссылка ) Здесь: Лемма 8, стр.119

[2] Бар-Хилель, Ю .; Перлз, М.; Шамир, Э. (1961), «О формальных свойствах грамматик простой фразовой структуры», Журнал фонетики, лингвистики и коммуникационных исследований , 14 (2): 143–172.

[3] Джон Э. Хопкрофт; Раджив Мотвани; Джеффри Д. Уллман (2003). Введение в теорию автоматов, языки и вычисления . Эддисон Уэсли. Здесь: разд.4.6, стр.166

[BLRS86-4] Берстель, Жан; Лауве, Аарон; Ройтенауэр, Кристоф; Салиола, Франко В. (2009). Комбинаторика слов. Слова Кристоффеля и повторы в словах . Серия монографий по CRM. Том. 27. Провиденс, Род-Айленд: Американское математическое общество . п. 86. ИСБН 978-0-8218-4480-9 . Артикул 1161.68043 .

[5] Савич, Уолтер (1982). Абстрактные машины и грамматики . п. 49 . ISBN 978-0-316-77161-0 .

[1]

[2]

[3]

[4]

[5]