Эффект Фойгта

Схема полярного эффекта Керра, продольного эффекта Керра и эффекта Фойгта

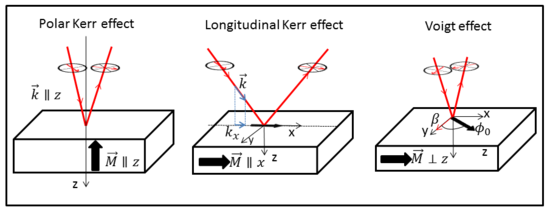
Эффект Фойгта — это магнитооптическое явление, которое вращает и эллипизирует линейно поляризованный свет, попадающий в оптически активную среду. Эффект назван в честь немецкого ученого Вольдемара Фойгта, открывшего его в парах . В отличие от многих других магнитооптических эффектов, таких как эффект Керра или Фарадея, которые линейно пропорциональны намагниченности (или приложенному магнитному полю для ненамагниченного материала), эффект Фойгта пропорционален квадрату намагниченности (или квадрату магнитное поле ) и его можно наблюдать экспериментально при нормальном падении. Существуют и другие названия этого эффекта, взаимозаменяемые в современной научной литературе: эффект Коттона-Мутона (в отношении французских ученых Эме Коттона и Анри Мутона открыли тот же эффект в жидкостях , которые несколько лет спустя ) и магнитно-линейное двойное лучепреломление. , причем последнее отражает физический смысл эффекта.

Для падающей электромагнитной волны линейно поляризованной ${\vec {E_{i}}}=(\cos \beta ,\,\sin \beta ,\,0)e^{-i\omega (t-n_{1}z/c)}$ и плоскополяризованный образец ${\vec {m}}=(\cos \phi ,\,\sin \phi ,\,0)$, выражение вращения в геометрии отражения имеет вид $\delta \beta$ является: $$\delta \beta _{r}={\frac {2\Delta n}{n_{0}^{2}-1}}\sin[2(\phi -\beta )]$$и в геометрии трансмиссии: $$\delta \beta _{t}={\frac {B_{1}+n_{0}^{2}{\Big [}{\frac {2L\omega }{c}}(1+n_{0})Q_{i}Q_{r}+Q_{r}^{2}-Q_{i}^{2}{\Big ]}}{n_{0}(1+n_{0})}},$$где ${\textstyle \Delta n={\frac {n_{\parallel }-n_{\perp }}{2}}}$ – разность показателей преломления в зависимости от параметра Фойгта $Q=Q_{i}+iQ_{r}$ (то же, что и для эффекта Керра), $n_{0}$ показатели преломления материала и $B_{1}$ параметр, ответственный за эффект Фойгта и поэтому пропорциональный $M^{2}$ или $(\mu _{0}H)^{2}$ в случае парамагнетика.

Подробный расчет и иллюстрация приведены в разделах ниже.

Теория

Рамки и система координат для вывода эффекта Фойгта. ${\vec {E}}_{i}$, ${\vec {E}}_{r}$ и ${\vec {E}}_{t}$ Имеются в виду падающее, отраженное и прошедшее электромагнитное поле.

Как и в случае с другими магнитооптическими эффектами, теория развивается стандартным образом с использованием эффективного диэлектрического тензора, на основе которого вычисляются собственные значения и собственные векторы систем. Как обычно, из этого тензора магнитооптические явления описываются преимущественно недиагональными элементами.

Здесь рассматривается падающая поляризация, распространяющаяся в направлении z: ${\vec {E_{i}}}=(\cos \beta ,\,\sin \beta ,\,0)e^{-i\omega (t-n_{1}z/c)}$ электрическое поле и однородно намагниченный в плоскости образец ${\vec {m}}=(\cos \phi ,\,\sin \phi ,\,0)$ где $\phi$ отсчет ведется от кристаллографического направления [100]. Цель состоит в том, чтобы вычислить ${\vec {E_{r}}}=(\cos \beta +\delta \beta ,\,\sin \beta +\delta \beta ,\,0)e^{-i\omega (t+n_{1}z/c)}$ где $\delta \beta$ это вращение поляризации из-за связи света с намагниченностью. Заметим, что $\delta \beta$ экспериментально представляет собой небольшую величину порядка мрад. ${\vec {m}}$ – вектор приведенной намагниченности, определяемый формулой ${\vec {m}}={\vec {M}}/M_{s}$ , $M_{s}$ намагниченность при насыщении. Мы подчеркнули, что именно потому, что вектор распространения света перпендикулярен плоскости намагничивания, можно увидеть эффект Фойгта.

Диэлектрический тензор

Следуя обозначениям Гильберта, обобщенный диэлектрический кубический тензор $\varepsilon _{r}$ принять следующую форму: $$(1)\qquad \varepsilon _{r}=\epsilon {\begin{bmatrix}1&0&iQm_{y}\\0&1&-iQm_{x}\\-iQm_{y}&iQm_{x}&1\end{bmatrix}}+{\begin{bmatrix}B_{1}m_{x}^{2}&B_{2}m_{x}m_{y}&0\\B_{2}m_{x}m_{y}&B_{1}m_{y}^{2}&0\\0&0&B_{1}m_{z}^{2}\end{bmatrix}}$$где $\varepsilon$ - диэлектрическая проницаемость материала, $Q$ параметр Фойгта, $B_{1}$ и $B_{2}$ две кубические константы, описывающие магнитооптический эффект в зависимости от $m_{i}^{2}$. $m_{i}$ это сокращение $m_{i}=M_{i}/M_{s}$. Расчет проведен в сферическом приближении с $B_{1}=B_{2}$. В настоящий момент, нет никаких доказательств того, что это приближение неверно, поскольку эффект Фойгта наблюдается редко, поскольку он чрезвычайно мал по сравнению с эффектом Керра.

Собственные значения и собственные векторы

Для расчета собственных значений и собственных векторов рассмотрим уравнение распространения, полученное из уравнений Максвелла, с соглашением ${\vec {n}}={\vec {k}}c/\omega$: $$(2)\qquad n^{2}{\vec {E}}-{\vec {n}}({\vec {n}}\cdot {\vec {E}})=\varepsilon {\vec {E}}$$

Когда намагниченность перпендикулярна волновому вектору распространения, в отличие от эффекта Керра, ${\vec {E}}$ все три его компонента могут быть равны нулю, что делает расчеты более сложными и делает уравнения Френеля недействительными. Способ упростить задачу состоит в использовании вектора смещения электрического поля ${\vec {D}}=\varepsilon {\vec {E}}$ . С ${\vec {\nabla }}\cdot {\vec {D}}=0$ и ${\vec {k}}\parallel {\vec {z}}$ у нас есть ${\vec {D}}=(D_{x},D_{y},0)$. Неудобно иметь дело с обратным диэлектрическим тензором, с которым может быть сложно справиться. Здесь расчет производится в общем случае, который математически сложен для обработки, однако демонстрацию можно легко проследить, рассмотрев $\phi =0$.

Собственные значения и собственные векторы находятся путем решения уравнения распространения на ${\vec {D}}$ что дает следующую систему уравнений: $$(3)\quad {\begin{cases}(\varepsilon _{xx}^{-1}-{\frac {1}{n^{2}}})D_{x}+\epsilon _{xy}^{-1}D_{y}=0\\\\\varepsilon _{yx}^{-1}D_{x}+(\varepsilon _{yy}^{-1}-{\frac {1}{n^{2}}})D_{y}=0\end{cases}}$$где $\varepsilon _{ij}^{-1}$ представляет собой обратную $ij$ элемент диэлектрического тензора $\varepsilon _{r}$, и $n^{2}=\varepsilon$. После непосредственной вычисления определителя системы необходимо сделать разложение 2-го порядка по $Q$ и первый заказ $B_{1}$. Это привело к двум собственным значениям, соответствующим двум показателям преломления: $$n_{\parallel }^{2}=\varepsilon +B_{1}$$$$n_{\perp }^{2}=\varepsilon (1-Q^{2})$$

Соответствующие собственные векторы для ${\vec {D}}$ и для ${\vec {E}}$ являются:

$$(4)\qquad {\vec {D}}_{\parallel }={\begin{pmatrix}\cos(\phi )\\\sin(\phi )\\0\end{pmatrix}}\qquad {\vec {D}}_{\perp }={\begin{pmatrix}-\sin(\phi )\\\cos(\phi )\\0\end{pmatrix}}\qquad {\vec {E}}_{\parallel }=\varepsilon ^{-1}{\vec {D}}_{\parallel }={\begin{pmatrix}{\frac {\cos(\phi )}{B_{1}+\varepsilon }}\\{\frac {\sin(\phi )}{B_{1}+\epsilon }}\\0\end{pmatrix}}\qquad {\vec {E}}_{\perp }=\varepsilon ^{-1}{\vec {D}}_{\perp }={\begin{pmatrix}{\frac {\sin(\phi )}{(Q^{2}-1)\epsilon }}\\{\frac {\cos(\phi )}{(1-Q^{2})\epsilon }}\\{\frac {-iQ}{(1-Q^{2})\epsilon }}\end{pmatrix}}$$

Геометрия отражения

Отношение непрерывности

Зная собственные векторы и собственные значения внутри материала, нужно вычислить ${\vec {E_{r}}}=(E_{rx},E_{ry},0)$ отраженный электромагнитный вектор обычно обнаруживается в экспериментах. Используем уравнения неразрывности для ${\vec {E}}$ и ${\vec {H}}$ где ${\vec {H}}$ - индукция, определяемая из уравнений Максвелла формулой ${\textstyle {\vec {\nabla }}\times {\vec {H}}={\frac {1}{c}}{\frac {\partial {\vec {D}}}{\partial t}}}$. Внутри среды электромагнитное поле разлагается на производные собственные векторы ${\vec {E}}_{t}=\alpha {\vec {E}}_{\parallel }+\beta {\vec {E}}_{\perp }$. Система уравнений, которую нужно решить: $$(5)\quad {\begin{cases}\alpha {\Big (}{\frac {D_{y\parallel }}{n_{\parallel }}}{\Big )}+\beta {\Big (}{\frac {D_{y\perp }}{n_{\perp }}}{\Big )}+E_{ry}=E_{0y}\\\\\alpha {\Big (}{\frac {D_{x\parallel }}{n_{\parallel }}}{\Big )}+\beta {\Big (}{\frac {D_{x\perp }}{n_{\perp }}}{\Big )}+E_{rx}=E_{0x}\\\\\alpha E_{x\parallel }+\beta E_{x\perp }-E_{rx}=E_{0x}\\\\\alpha E_{y\parallel }+\beta E_{y\perp }-E_{ry}=E_{0y}\end{cases}}$$

Решением этой системы уравнений являются: $$(6)\quad E_{rx}=E_{0}{\frac {(1-n_{\perp }n_{\parallel })\cos(\beta )+(n_{\perp }-n_{\parallel })\cos(\beta -2\phi )}{(1+n_{\parallel })(1+n_{\perp })}}$$$$(7)\quad E_{ry}=E_{0}{\frac {(1-n_{\perp }n_{\parallel })\sin(\beta )-(n_{\perp }-n_{\parallel })\sin(\beta -2\phi )}{(1+n_{\parallel })(1+n_{\perp })}}$$

Расчет угла поворота

Угол поворота $\delta \beta$ и угол эллиптичности $\psi$ определяются из соотношения $\chi =E_{ry}/E_{rx}$ с помощью двух следующих формул: $$(8)\quad \tan 2\delta \beta ={\frac {2\operatorname {Re} (\chi )}{1-|\chi |^{2}}}\qquad (9)\quad \sin(2\psi _{K})={\frac {2\operatorname {Im} (\chi )}{1-|\chi |^{2}}},$$где $\operatorname {Re} (\chi )$ и $\operatorname {Im} (\chi )$ представляют действительную и мнимую часть $\chi$. Используя две ранее рассчитанные компоненты, получаем: $$(10)\qquad \chi ={\frac {(B_{1}+n_{0}^{2}Q^{2})}{2n_{0}(n_{0}^{2}-1)}}{\frac {\sin[2(\phi -\beta )]}{\cos(\beta )^{2}}}+\tan(\beta ).$$ Это дает для вращения Фойгта: $$(11)\qquad \delta \beta =\operatorname {Re} \left[{\frac {B_{1}+n_{0}^{2}Q^{2}}{2n_{0}(n_{0}^{2}-1)}}\right]\sin[2(\phi -\beta )],$$ которое также можно переписать в случае $B_{1}$, $n_{0}$, и $Q$ настоящий: $$(12)\quad \delta \beta ={\frac {2\Delta n}{n_{0}^{2}-1}}\sin[2(\phi -\beta )],$$ где $\Delta n={\frac {n_{\parallel }-n_{\perp }}{2}}$ – разность показателей преломления. Следовательно, получается нечто пропорциональное $\Delta n$ и которая зависит от падающей линейной поляризации. Для правильного $\phi -\beta$ никакого вращения Фойгта не наблюдается. $\Delta n$ пропорциональна квадрату намагниченности, поскольку $B_{1}\propto M_{s}^{2}$ и $Q\propto M_{s}$.

Геометрия трансмиссии

Расчет вращения эффекта Фойгта при передаче в принципе эквивалентен расчету эффекта Фарадея. На практике эта конфигурация вообще не используется для ферромагнитных образцов, поскольку длина поглощения в этом материале мала. Однако использование геометрии пропускания более распространено для парамагнитной жидкости или кристалла, где свет может легко перемещаться внутри материала.

Расчет для парамагнетика точно такой же, как и для ферромагнитного, за исключением того, что намагниченность заменяется полем $\mu _{0}{\vec {H}}=\mu _{0}H_{0}(\cos \phi ,\,\sin \phi )$ ( $H_{0}$ в $\mathrm {A/m}$ или $\mathrm {G}$). Для удобства поле будет добавлено в конце расчета в магнитооптических параметрах.

Рассмотрим передаваемые электромагнитные волны ${\vec {E}}_{t}$ распространяющийся в среде длиной L. Из уравнения (5) получаем для $\alpha$ и $\beta$: $$\alpha ={\frac {2E_{0}n_{\parallel }\cos(\theta -\phi )}{1+n_{\parallel }}}$$$$\beta ={\frac {2E_{0}n_{\perp }^{2}\sin(\theta -\phi )}{n_{\perp }+1}}$$В позиции z = L выражение ${\vec {E}}_{t}$ является: $$(13)\quad {\vec {E}}_{t}=e^{-i\omega [t+{\frac {(n_{\parallel }+n_{\perp })L}{2c}}]}{\Big [}\alpha {\vec {E}}_{\parallel }e^{i{\frac {\omega \Delta nL}{c}}}+\beta {\vec {E}}_{\perp }e^{-i{\frac {\omega \Delta nL}{c}}}{\Big ]}$$где ${\vec {E}}_{\parallel }$ и ${\vec {E}}_{\perp }$— собственные векторы, вычисленные ранее, и $\Delta n={\frac {n_{\parallel }-n_{\perp }}{2}}$ – это разница двух показателей преломления. Затем вращение рассчитывается из соотношения $\chi ={\frac {E_{t_{y}}}{E_{t_{x}}}}$, с развитием в первом порядке в $B_{1}$ и второй порядок в $Q$. Это дает: $$(14)\quad \chi ={\frac {c-i~\omega L(1+n_{0})(B_{1}+n_{0}Q^{2})\sin[2(\beta -\phi )]}{4cn_{0}(1+n_{0})\cos ^{2}(\beta )}}={\frac {c-i~\omega L(1+n_{0})\Delta n\sin[2(\beta -\phi )]}{c~(1+n_{0})\cos ^{2}(\beta )}}$$

Снова мы получаем нечто пропорциональное $\Delta n$ и $L$, длина распространения света. Заметим, что $\Delta n$ пропорционально $(\mu _{0}H_{0})^{2}$ таким же образом и относительно геометрии, отражающей намагниченность. Чтобы извлечь вращение Фойгта, мы рассмотрим $n_{0}=\eta +i~\kappa$, $Q=Q_{r}+i~Q_{i}$ и $B_{1}$ настоящий. Затем нам нужно вычислить действительную часть (14). Полученное выражение затем подставляется в (8). В приближении отсутствия поглощения для вращения Фойгта в геометрии пропускания получаем: $$(15)\quad \delta \beta =(\mu _{0}H)^{2}{\frac {B_{1}+n_{0}^{2}{\Big [}{\frac {2L\omega }{c}}(1+n_{0})Q_{i}Q_{r}+Q_{r}^{2}-Q_{i}^{2}{\Big ]}}{n_{0}(1+n_{0})}}$$

Иллюстрация эффекта Фойгта в GaMnAs

Рис. 1: а) Экспериментальный цикл гистерезиса на плоском образце (Ga,Mn)As. б) Цикл гистерезиса Фойгта, полученный путем извлечения симметричной части (а). в) Продольный Керр, полученный путем выделения асимметричной части (а)

Рис. 2: а) Механизм переключения плоского образца (Ga,Mn)As для магнитного поля, приложенного вдоль оси [1-10] при температуре 12 К. б) Сигнал Фойгта, смоделированный с помощью механизма, показанного на а)

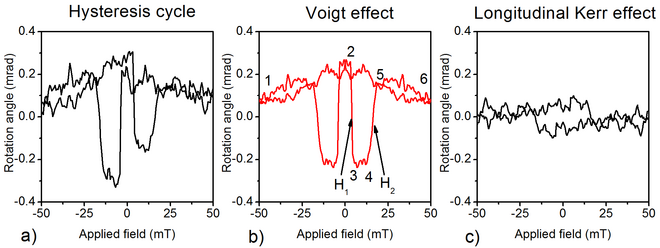
В качестве иллюстрации применения эффекта Фойгта приведем пример в магнитном полупроводнике (Ga,Mn)As, где наблюдался большой эффект Фойгта. При низких температурах (в основном для $T<{\frac {T_{c}}{2}}$) для материала с намагниченностью в плоскости (Ga,Mn)As демонстрирует двухосную анизотропию с намагниченностью, ориентированной вдоль (или близкого к) направлений <100>.

Типичный гистерезисный цикл, содержащий эффект Фойгта, показан на рисунке 1. Этот цикл был получен путем направления линейно поляризованного света вдоль направления [110] с углом падения примерно 3° (более подробную информацию можно найти в ) и измерение вращения за счет магнитооптических эффектов отраженного светового луча. В отличие от обычного продольного/полярного эффекта Керра, цикл гистерезиса равномерен по отношению к намагниченности, что является признаком эффекта Фойгта. Этот цикл был получен при падении света, очень близком к нормальному, и в нем также присутствует небольшая нечетная часть; необходимо провести правильную обработку, чтобы выделить симметричную часть гистерезиса, соответствующую эффекту Фойгта, и асимметричную часть, соответствующую продольному эффекту Керра.

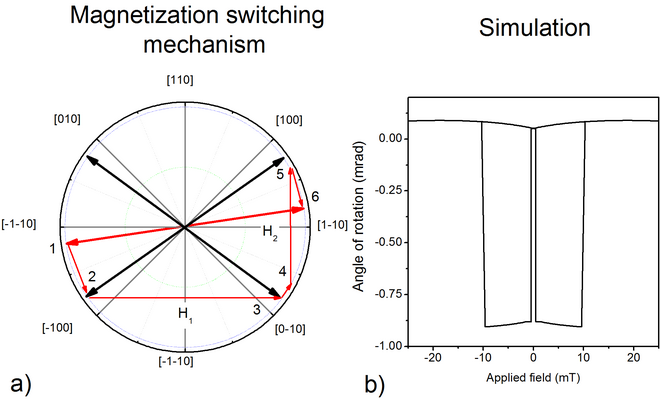
В представленном здесь случае гистерезиса поле прикладывалось в направлении [1-10]. Механизм переключения следующий:

1. Мы начинаем с сильного отрицательного поля и намагниченности, близкой к направлению [-1-10] в положении 1.
2. Магнитное поле уменьшается, что приводит к когерентному повороту намагниченности от 1 до 2.
3. В положительном поле намагниченность резко переключается с 2 на 3 за счет зарождения и распространения магнитных доменов, создавая первое коэрцитивное поле, названное здесь. $H_{1}$
4. Намагниченность остается близкой к состоянию 3, при этом когерентно вращаясь к состоянию 4, расположенному ближе к направлению приложенного поля.
5. И снова намагниченность резко переключается с 4 на 5 в результате зарождения и распространения магнитных доменов. Это переключение происходит из-за того, что конечное положение равновесия находится ближе от состояния 5 к состоянию 4 (и поэтому его магнитная энергия ниже). Это дает еще одно принудительное поле под названием $H_{2}$
6. Наконец, намагниченность когерентно вращается из состояния 5 в состояние 6.

Моделирование этого сценария представлено на рисунке 2, где $$\operatorname {Re} \left[{\frac {B_{1}+n_{0}^{2}Q^{2}}{2n_{0}(n_{0}^{2}-1)}}\right]P_{\text{Voigt}}=0.5\,\mathrm {mrad} .$$Как видно, смоделированный гистерезис качественно не отличается от экспериментального. Обратите внимание, что амплитуда при $H_{1}$ или $H_{2}$ примерно в два раза больше $P_{\text{Voigt}}$

См. также

• Атомный сетевой фильтр
• Эффект хлопка-мутона
• Эффект Фарадея

Дальнейшее чтение

• Чжао, Чжун-Цюань. Атомные линейные фильтры в возбужденном состоянии . Проверено 26 марта 2006 г.