Система подобия треугольников

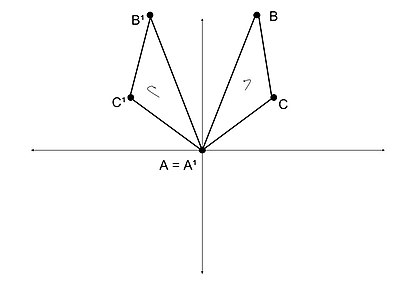
Система подобия треугольников — это определенная конфигурация, включающая набор треугольников. ^[1] Набор треугольников считается конфигурацией , когда все треугольники имеют как минимум одно отношение инцидентности с одним из других треугольников, присутствующих в наборе. ^[1] Отношение инцидентности между треугольниками означает, что два треугольника имеют общую точку. Например, два треугольника справа, $AHC$ и $BHC$ , представляют собой конфигурацию, состоящую из двух инцидентных отношений, поскольку точки $C$ и $H$ являются общими. Треугольники, составляющие конфигурации, называются составными треугольниками. ^[1] Чтобы попасть в систему подобия, треугольники должны быть не только частью набора конфигураций, но и быть непосредственно подобными. ^[1] Прямое подобие подразумевает, что все углы между двумя данными треугольниками равны и что они имеют одинаковое направление вращения. ^[2] Как видно на соседних изображениях, в прямоподобных треугольниках вращение $B$ на $C$ и $B^{1}$ на $C^{1}$ происходит в том же направлении. В противоположных подобных треугольниках вращение $B$ на $C$ и $B^{1}$ на $C^{1}$ происходит в противоположном направлении. В целом, конфигурация представляет собой систему подобия, когда все треугольники в наборе лежат в одной плоскости и справедливо следующее: если n в наборе треугольников и n - 1 треугольников прямо подобны, то n треугольников прямо подобны. . ^[1]

Фон

Дж. Г. Молдон представил идею систем подобия треугольников в своей статье в журнале Mathematics Magazine «Подобные треугольники». ^[1] Молдон начал свой анализ с рассмотрения заданных треугольников. $ABC,XYZ$ для прямого сходства через комплексные числа, в частности уравнение ${\begin{vmatrix}a&b&c\\x&y&z\\1&1&1\end{vmatrix}}=0$ . ^[1] Затем он продолжил свой анализ равносторонних треугольников, показав, что если треугольник $ABC$ удовлетворяет уравнению $a+wb+w^{2}c=0$ когда $w={\frac {-1+i\surd 3}{2}}$ , оно было равносторонним. ^[1] В качестве доказательства этой работы он применил свои гипотезы о прямом подобии и равносторонних треугольниках при доказательстве теоремы Наполеона . ^[1] Затем он построил Наполеона, доказав, что если бы равносторонний треугольник был построен с равносторонними треугольниками, инцидентными каждой вершине, то средние точки соединительных линий между неинцидентными вершинами трех внешних равносторонних треугольников образуют равносторонний треугольник. ^[1] Другая аналогичная работа была проделана французским геометром Тебо в его доказательстве того, что при наличии параллелограмма и квадратов, лежащих на каждой стороне параллелограмма, центры квадратов образуют квадрат. ^[3] Затем Молдон проанализировал компланарные множества треугольников, определяя, являются ли они системами подобия на основе критерия: если все треугольники, кроме одного, были прямо подобны, то все треугольники напрямую подобны. ^[1]

Примеры

Треугольники, добавленные к прямоугольнику

Прямое сходство

Если мы построим прямоугольник $ABCD$ с прямо подобными треугольниками $PAB,QBC,RCD,SDA$ на каждой стороне прямоугольника, подобные $PQS$ , затем $RQS$ прямо подобен, а множество треугольников $\{PAB,QBC,RCD,SDA,PQS,RQS\}$ это система подобия. ^[1]

Косвенное сходство

Однако если признать, что треугольники могут быть вырождены и принимать точки $B$ и $P$ лежать друг на друге и $Q,R,D$ и $S$ лежать друг на друге, то множество треугольников уже не является системой прямого подобия, так как второй треугольник имеет площадь, а остальные нет. ^[1]

Прямоугольный параллелепипед

Дана фигура, на которой три набора прямых параллельны, но не эквивалентны по длине (формально известная как прямоугольный параллелепипед ), причем все точки второго порядка помечены следующим образом:

\{A_{1}B_{1}C_{1},A_{2}B_{2}C_{2},A_{3}B_{3}C_{3},A_{4}B_{4}C_{4},A_{1}B_{4}C_{3},A_{2}B_{3}C_{4},A_{3}B_{2}C_{1},A_{4}B_{1}C_{2}\}

Затем мы можем взять вышеуказанные точки, проанализировать их как треугольники и показать, что они образуют систему подобия. ^[1]

Доказательство:

Чтобы для любого заданного треугольника $KLM$ , чтобы быть непосредственно похожим на $A_{1},B_{1},C_{1}$ должно выполняться следующее уравнение:

(\ell -m)a_{1}+(m-k)b_{1}+(k-1)c_{1}=0.

^[1] где ℓ , m , k , a1 _c1 , b1 _и — стороны _. треугольников

Если проследить ту же схему для остальных треугольников, можно заметить, что суммирование уравнений для первых четырех треугольников и суммирование уравнений для последних четырех треугольников дает один и тот же результат. ^[1] Следовательно, по определению системы подобия треугольников, независимо от того, будут ли выбраны семь подобных треугольников, восьмой будет удовлетворять системе, делая их всех непосредственно подобными. ^[1]

Галерея

Пример прямого сходства
Между треугольниками AHC и BHC существуют два инцидентных отношения.
Пример противоположного сходства
Теорема Тебо
Теорема Наполеона
Пример системы подобия
Пример системы несходства
Прямоугольный параллелепипед

Ссылки

^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот ^п ^д Молдон, Дж. Г. (май 1966 г.). «Подобные треугольники». Журнал «Математика» . 39 (3): 165–174. дои : 10.1080/0025570X.1966.11975709 .
^ Вайсштейн, Эрик. "Похожий" . Вольфрам Математический мир . Проверено 12 декабря 2018 г.
^ Гербер, Леон (октябрь 1980 г.). «Теорема Наполеона и неравенство параллелограмма для аффинно-правильных многоугольников». Американский математический ежемесячник . 87 (8): 644–648. дои : 10.1080/00029890.1980.11995110 . JSTOR 2320952 .

[:0-1] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот ^п ^д Молдон, Дж. Г. (май 1966 г.). «Подобные треугольники». Журнал «Математика» . 39 (3): 165–174. дои : 10.1080/0025570X.1966.11975709 .

[:2-2] Вайсштейн, Эрик. "Похожий" . Вольфрам Математический мир . Проверено 12 декабря 2018 г.

[:1-3] Гербер, Леон (октябрь 1980 г.). «Теорема Наполеона и неравенство параллелограмма для аффинно-правильных многоугольников». Американский математический ежемесячник . 87 (8): 644–648. дои : 10.1080/00029890.1980.11995110 . JSTOR 2320952 .

[1]

[2]

[3]