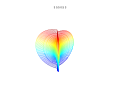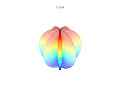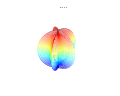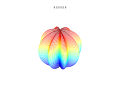Суперформула

Суперформула и обобщением суперэллипса является была предложена Йоханом Гиелисом около 2000 года. ^[1] Гилис предположил, что эту формулу можно использовать для описания многих сложных форм и кривых, встречающихся в природе. Гилис подал заявку на патент, связанный с синтезом шаблонов, созданных с помощью суперформулы, срок действия которой истек 10 мая 2020 г. ^[2]

В полярных координатах , с $r$ радиус и $\varphi$ угол, суперформула:

$r\left(\varphi \right)=\left(\left|{\frac {\cos \left({\frac {m\varphi }{4}}\right)}{a}}\right|^{n_{2}}+\left|{\frac {\sin \left({\frac {m\varphi }{4}}\right)}{b}}\right|^{n_{3}}\right)^{-{\frac {1}{n_{1}}}}.$ Выбирая разные значения параметров $a,b,m,n_{1},n_{2},$ и $n_{3},$ можно создавать разные формы.

Формула была получена путем обобщения суперэллипса, названного и популяризированного Питом Хейном , датским математиком .

2D-графики

В следующих примерах значения, показанные над каждым рисунком, должны быть m , n ₁ , n ₂ и n ₃ .

Программа GNU Octave для создания этих цифр.

function sf2d(n, a)
  u = [0:.001:2 * pi];
  raux = abs(1 / a(1) .* abs(cos(n(1) * u / 4))) .^ n(3) + abs(1 / a(2) .* abs(sin(n(1) * u / 4))) .^ n(4);
  r = abs(raux) .^ (- 1 / n(2));
  x = r .* cos(u);
  y = r .* sin(u);
  plot(x, y);
end

Расширение до более высоких измерений

Формулу можно расширить до 3, 4 или n измерений с помощью сферического произведения суперформул. Например, параметрическая 3D -поверхность получается перемножением двух суперформул r ₁ и r ₂ . Координаты определяются соотношениями:

$x=r_{1}(\theta )\cos \theta \cdot r_{2}(\phi )\cos \phi ,$ $y=r_{1}(\theta )\sin \theta \cdot r_{2}(\phi )\cos \phi ,$ $z=r_{2}(\phi )\sin \phi ,$

где $\phi$ ( широта ) варьируется между - π /2 и π /2, а θ ( долгота ) между - π и π .

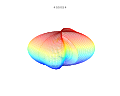
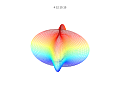
3D сюжет

3D-суперформула: a = b = 1; m , n ₁ , n ₂ и n ₃ показаны на рисунках.

Программа GNU Octave для создания этих цифр:

function sf3d(n, a)
  u = [- pi:.05:pi];
  v = [- pi / 2:.05:pi / 2];
  nu = length(u);
  nv = length(v);
  for i = 1:nu
    for j = 1:nv
      raux1 = abs(1 / a(1) * abs(cos(n(1) .* u(i) / 4))) .^ n(3) + abs(1 / a(2) * abs(sin(n(1) * u(i) / 4))) .^ n(4);
      r1 = abs(raux1) .^ (- 1 / n(2));
      raux2 = abs(1 / a(1) * abs(cos(n(1) * v(j) / 4))) .^ n(3) + abs(1 / a(2) * abs(sin(n(1) * v(j) / 4))) .^ n(4);
      r2 = abs(raux2) .^ (- 1 / n(2));
      x(i, j) = r1 * cos(u(i)) * r2 * cos(v(j));
      y(i, j) = r1 * sin(u(i)) * r2 * cos(v(j));
      z(i, j) = r2 * sin(v(j));
    endfor;
  endfor;
  mesh(x, y, z);
endfunction;

Обобщение

Суперформулу можно обобщить, допустив различные m параметров в двух членах суперформулы. Заменив первый параметр $m$ с y и вторым параметром $m$ с г : ^[3] $r\left(\varphi \right)=\left(\left|{\frac {\cos \left({\frac {y\varphi }{4}}\right)}{a}}\right|^{n_{2}}+\left|{\frac {\sin \left({\frac {z\varphi }{4}}\right)}{b}}\right|^{n_{3}}\right)^{-{\frac {1}{n_{1}}}}$

Это позволяет создавать вращательно-асимметричные и вложенные структуры. В следующих примерах а, б, ${n_{2}}$ и ${n_{3}}$ 1:

Ссылки

^ Гиелис, Йохан (2003), «Общее геометрическое преобразование, объединяющее широкий спектр естественных и абстрактных форм» , American Journal of Botany , 90 (3): 333–338, doi : 10.3732/ajb.90.3.333 , ISSN 0002 -9122 , PMID 21659124
^ Патент EP 1177529 , Гилис, Йохан, «Способ и устройство для синтеза рисунков», выдан 2 февраля 2005 г.
^ * Штёр, Уве (2004 г.), SuperformulaU (PDF) , заархивировано из оригинала (PDF) 8 декабря 2017 г.

Внешние ссылки

[1] Гиелис, Йохан (2003), «Общее геометрическое преобразование, объединяющее широкий спектр естественных и абстрактных форм» , American Journal of Botany , 90 (3): 333–338, doi : 10.3732/ajb.90.3.333 , ISSN 0002 -9122 , PMID 21659124

[2] Патент EP 1177529 , Гилис, Йохан, «Способ и устройство для синтеза рисунков», выдан 2 февраля 2005 г.

[3] * Штёр, Уве (2004 г.), SuperformulaU (PDF) , заархивировано из оригинала (PDF) 8 декабря 2017 г.

[1]

[2]

[3]