Планарный САТ

Пример планарной задачи SAT. Черные ребра соответствуют неинвертированным переменным, а красные ребра соответствуют инвертированным переменным.

В информатике плоская проблема 3-выполнимости (сокращенно PLANAR 3SAT или PL3SAT ) представляет собой расширение классической булевой проблемы 3-выполнимости до плоского графа инцидентности . Другими словами, он спрашивает, могут ли переменные данной логической формулы, график инцидентности которой, состоящий из переменных и предложений, может быть встроен в плоскость , последовательно заменены значениями ИСТИНА или ЛОЖЬ таким образом, чтобы формула имела значение ИСТИНА. . В этом случае формула называется выполнимой . С другой стороны, если такого присвоения не существует, функция, выраженная формулой, является ЛОЖНОЙ для всех возможных присвоений переменных, и формула является невыполнимой . Например, формула « a AND NOT b » выполнима, поскольку можно найти значения a = TRUE и b = FALSE, которые делают ( a AND NOT b ) = TRUE. Напротив, выражение « А И НЕ а » невыполнимо.

Как и 3SAT , PLANAR-SAT является NP-полным и обычно используется при сокращениях .

Определение

Любую задачу 3SAT можно преобразовать в граф заболеваемости следующим образом: Для каждой переменной $v_{i}$, граф имеет один соответствующий узел $v_{i}$, и для каждого предложения $c_{j}$, граф имеет один соответствующий узел $c_{j}.$ Край $(v_{i},c_{j})$ создается между переменной $v_{i}$ и пункт $c_{j}$ в любое время $v_{i}$ или $\lnot v_{i}$ находится в $c_{j}$. Положительные и отрицательные литералы различаются с помощью раскраски ребер .

Формула выполнима тогда и только тогда, когда существует способ присвоить ИСТИНА или ЛОЖЬ каждому узлу переменной, так что каждый узел предложения соединен хотя бы с одним ИСТИНА положительным ребром или ЛОЖЬ отрицательным ребром.

Планарный граф — это граф, который можно нарисовать на плоскости так, чтобы никакие два его ребра не пересекались. Планарный 3SAT — это подмножество 3SAT, в котором граф инцидентности переменных и предложений булевой формулы является плоским. Это важно, поскольку это ограниченный вариант, который по-прежнему NP-полный. Многие задачи (например, игры и головоломки) не могут представлять собой неплоские графы. Следовательно, Planar 3SAT дает возможность доказать NP-сложность этих задач.

Доказательство NP-полноты

Левая сторона — переезд; правая сторона — гаджет-кроссовер. Маленькие точки обозначают пункты. Черные и красные края соответствуют неинвертированным и инвертированным переменным соответственно.

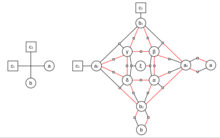
Следующий эскиз доказательства следует доказательству Д. Лихтенштейна.

Тривиально, PLANAR 3SAT находится в NP . Таким образом, достаточно показать, что это NP-трудно, путем редукции от 3SAT .

В этом доказательстве используется тот факт, что $(\lnot a\lor \lnot b\lor c)\land (a\lor \lnot c)\land (b\lor \lnot c)$ эквивалентно $(a\land b)\leftrightarrow c$ и это $(a\lor \lnot b)\land (\lnot a\lor b)$ эквивалентно $a\leftrightarrow b$.

Сначала нарисуйте график заболеваемости формулы 3SAT. Поскольку никакие две переменные или предложения не связаны между собой, результирующий граф будет двудольным . Предположим, что полученный граф не является плоским. каждого пересечения ребер ( , c1 ) _Для и ( b , c2 _{пересечение} ) введите девять новых переменных , _, α , _β γ , δ , ξ , a2 a1 a , b2 и _{замените} , каждое _b1 ребер края с помощью кроссовера, показанного на схеме. Он состоит из следующих новых положений:

$${\begin{array}{ll}(\lnot a_{2}\lor \lnot b_{2}\lor \alpha )\land (a_{2}\lor \lnot \alpha )\land (b_{2}\lor \lnot \alpha ),&\quad {\text{i.e.,}}\quad a_{2}\land b_{2}\leftrightarrow \alpha \\(\lnot a_{2}\lor b_{1}\lor \beta )\land (a_{2}\lor \lnot \beta )\land (\lnot b_{1}\lor \lnot \beta ),&\quad {\text{i.e.,}}\quad a_{2}\land \lnot b_{1}\leftrightarrow \beta \\(a_{1}\lor b_{1}\lor \gamma )\land (\lnot a_{1}\lor \lnot \gamma )\land (\lnot b_{1}\lor \lnot \gamma ),&\quad {\text{i.e.,}}\quad \lnot a_{1}\land \lnot b_{1}\leftrightarrow \gamma \\(a_{1}\lor \lnot b_{2}\lor \delta )\land (\lnot a_{1}\lor \lnot \delta )\land (b_{2}\lor \lnot \delta ),&\quad {\text{i.e.,}}\quad \lnot a_{1}\land b_{2}\leftrightarrow \delta \\(\alpha \lor \beta \lor \xi )\land (\gamma \lor \delta \lor \lnot \xi ),&\quad {\text{i.e.,}}\quad \alpha \lor \beta \lor \gamma \lor \delta \\(\lnot \alpha \lor \lnot \beta )\land (\lnot \beta \lor \lnot \gamma )\land (\lnot \gamma \lor \lnot \delta )\land (\lnot \delta \lor \lnot \alpha ),&\\(a_{2}\lor \lnot a)\land (a\lor \lnot a_{2})\land (b_{2}\lor \lnot b)\land (b\lor \lnot b_{2}),&\quad {\text{i.e.,}}\quad a\leftrightarrow a_{2},~b\leftrightarrow b_{2}\\\end{array}}$$

Если ребро ( a , c ₁ ) инвертировано в исходном графе, ( a ₁ , c ₁ ) должно быть инвертировано в гаджете кроссовера. Аналогично, если ребро ( b , c ₂ ) перевернуто в оригинале, ( b ₁ , c ₂ ) должно быть перевернуто.

Легко показать, что эти условия выполнимы тогда и только тогда, когда $a\leftrightarrow a_{1}$ и $b\leftrightarrow b_{1}$.

Этот алгоритм показывает, что можно преобразовать каждое пересечение в его планарный эквивалент, используя только постоянное количество новых дополнений. Поскольку количество пересечений полиномиально по количеству предложений и переменных, сокращение является полиномиальным.

Варианты и связанные с ними проблемы

• Планарный 3SAT с переменным циклом : Здесь, помимо графа инцидентности, граф также включает в себя цикл, проходящий через все переменные, и каждое предложение находится либо внутри, либо вне этого цикла. Полученный граф по-прежнему должен быть плоским. Эта задача является NP-полной.
  • Однако, если проблема дополнительно ограничена таким образом, что все предложения находятся внутри переменного цикла или все предложения находятся вне его, тогда проблема может быть решена за полиномиальное время с использованием динамического программирования .
• Планарный 3SAT с литералами : двудольный граф инцидентности литералов и предложений также является плоским. Эта задача является NP-полной.
• Плоский прямолинейный 3SAT : Вершины графа представлены в виде горизонтальных сегментов. Каждая переменная расположена на оси x , а каждое предложение находится выше/ниже оси x . Каждое соединение между переменной и предложением должно быть вертикальным сегментом. Каждое предложение может иметь не более трех связей с переменными и быть либо полностью положительными, либо полностью отрицательными. Эта задача является NP-полной.
  • Плоский монотонный прямолинейный 3SAT : это вариант плоского прямолинейного 3SAT, в котором предложения над осью X являются полностью положительными, а положения ниже оси X - полностью отрицательными. Эта задача NP-полна. и остается NP-полным, когда каждое предложение, содержащее три переменные, имеет две соседние переменные, соседние по оси x (т. е. никакая другая переменная не появляется горизонтально между соседними переменными).
• Планарный 1-в-3SAT : это плоский эквивалент 1-в-3SAT . Он NP-полный.
  • Плоский положительный прямолинейный 1-в-3SAT : это плоский эквивалент положительного 1-в-3SAT . Он NP-полный.
• Планарный NAE 3SAT : Эта задача является плоским эквивалентом NAE 3SAT . В отличие от других вариантов, эту задачу можно решить за полиномиальное время . Доказательство проводится сведением к плоскому максимальному разрезу .
• Планарная схема SAT : это вариант схемы SAT , в которой схема, вычисляющая формулу SAT, представляет собой планарный ориентированный ациклический граф . Обратите внимание, что это другой график, чем граф смежности формулы. Эта задача является NP-полной.

Скидки

Логические головоломки

Редукция из Planar SAT - это широко используемый метод доказательства NP-полноты логических головоломок. Примеры: Филломино , Нурикабе , Шакашака , Татамибари , и Тентай Шоу . Эти доказательства включают в себя создание устройств, которые могут имитировать провода, передающие сигналы (логические значения), входные и выходные вентили, разделители сигналов, вентили НЕ и вентили И (или ИЛИ), чтобы представить планарное вложение любой булевой схемы. Поскольку схемы плоские, пересечение проводов учитывать не нужно.

Плоское складывание цепей с фиксированным углом

Это проблема определения того, имеет ли многоугольная цепь с фиксированными длинами ребер и углами плоскую конфигурацию без пересечений. Было доказано, что он сильно NP-труден за счет сокращения плоского монотонного прямолинейного 3SAT.

Перегородка с минимальной длиной ребра

Это проблема разбиения многоугольника на более простые многоугольники так, чтобы общая длина всех ребер, используемых в разбиении, была как можно меньше.

Если фигура представляет собой прямолинейный многоугольник и его следует разбить на прямоугольники, а многоугольник не содержит дырок, то задача является полиномиальной. Но если он содержит дыры (даже вырожденные дырки — отдельные точки), проблема является NP-трудной, если исходить из Planar SAT. То же самое справедливо, если фигура представляет собой любой многоугольник и его следует разбить на выпуклые фигуры.

Связанной проблемой является триангуляция с минимальным весом - поиск триангуляции с минимальной общей длиной ребра. Доказано, что версия решения этой задачи является NP-полной за счет сокращения варианта Planar 1-in-3SAT.