Минимальное отклонение

В призме угол отклонения ( $δ$ ) уменьшается с увеличением угла падения ( $i$ ) до определенного угла. Этот угол падения, при котором угол отклонения призмы минимален, называется положением минимального отклонения призмы, а сам этот угол отклонения известен как минимальный угол отклонения (обозначается $δ min$ , $D λ$ или $D m$ ).

Угол минимального отклонения связан с показателем преломления следующим образом:

$n_{21}={\dfrac {\sin \left({\dfrac {A+D_{m}}{2}}\right)}{\sin \left({\dfrac {A}{2}}\right)}}$

Это полезно для расчета показателя преломления материала. Радуга и гало возникают при минимальном отклонении. Также тонкая призма всегда выставлена на минимальное отклонение.

Формула

При минимальном отклонении преломленный луч в призме параллелен ее основанию. Другими словами, луч света симметричен относительно оси симметрии призмы. ^[1]^[2]^[3] Также углы преломления равны, т.е. $r 1 = r 2$ . Угол падения и угол выхода равны друг другу ( $i = e$ ). Это хорошо видно на графике ниже.

Формулу минимального отклонения можно вывести, используя геометрию призмы. Подход предполагает замену переменных в законе Снелла на углы отклонения и призмы, используя вышеуказанные свойства.

Из суммы углов ${\textstyle \triangle OPQ}$ ,

$A+\angle OPQ+\angle OQP=180^{\circ }$ $\implies A=180^{\circ }-(90-r)-(90-r)$ $\implies r={\frac {A}{2}}$

Используя теорему о внешнем угле в ${\textstyle \triangle PQR}$ ,

$D_{m}=\angle RPQ+\angle RQP$ $\implies D_{m}=i-r+i-r$ $\implies 2r+D_{m}=2i$ $\implies A+D_{m}=2i$ $\implies i={\frac {A+D_{m}}{2}}$

Это также можно получить, поместив $i = e$ в формулу призмы : $i + e = A + δ.$

Из Снеллиуса закона

$n_{21}={\dfrac {\sin i}{\sin r}}$

$\therefore n_{21}={\dfrac {\sin \left({\dfrac {A+D_{m}}{2}}\right)}{\sin \left({\dfrac {A}{2}}\right)}}$ ^[4]^[3]^[1]^[2]^[5]^{[ чрезмерное цитирование ]}

$\therefore D_{m}=2\sin ^{-1}\left(n\sin \left({\frac {A}{2}}\right)\right)-A$

(где $n$ — показатель преломления, $A$ — угол призмы, а $D m$ — минимальный угол отклонения.)

Это удобный способ измерения показателя преломления материала (жидкости или газа) путем направления луча света через призму незначительной толщины с минимальным отклонением, заполненную материалом, или через погруженную в него стеклянную призму. ^[5]^[3]^[1]

Проработанные примеры:

Показатель преломления стекла равен 1,5. Желателен минимальный угол отклонения равносторонней призмы вместе с соответствующим углом падения.

Answer: 37°, 49°

Solution:

Here, $A = 60°$ , $n = 1.5$

Plugging them in the above formula,

${\textstyle {\frac {\sin \left({\frac {60+\delta }{2}}\right)}{\sin \left({\frac {60}{2}}\right)}}=1.5}$

${\textstyle \implies {\frac {\sin \left(30+{\frac {\delta }{2}}\right)}{\sin(30)}}=1.5}$

${\textstyle \implies \sin \left(30+{\frac {\delta }{2}}\right)=1.5\times 0.5}$

${\textstyle \implies 30+{\frac {\delta }{2}}=\sin ^{-1}(0.75)}$

${\textstyle \implies {\frac {\delta }{2}}=48.6-30}$

${\textstyle \implies \delta =2\times 18.6}$

${\textstyle \therefore \delta \approx 37^{\circ }}$

Also,

${\textstyle i={\frac {(A+\delta )}{2}}={\frac {60+2\times 18.6}{2}}\approx 49^{\circ }}$

This is also apparent in the graph below.

Если минимальный угол отклонения призмы с показателем преломления 1,4 равен ее углу преломления, угол призмы желателен.

Answer: 60°

Solution:

Here, ${\textstyle \delta =r}$

${\textstyle \implies \delta ={\frac {A}{2}}}$

Using the above formula,

${\textstyle {\frac {\sin \left({\frac {A+{\frac {A}{2}}}{2}}\right)}{\sin \left({\frac {A}{2}}\right)}}=1.4}$

${\textstyle \implies {\frac {\sin \left({\frac {3A}{4}}\right)}{\sin \left({\frac {A}{2}}\right)}}={\frac {\frac {1}{2}}{\frac {1}{\sqrt {2}}}}}$

${\textstyle \implies {\frac {\sin \left({\frac {3A}{4}}\right)}{\sin \left({\frac {A}{2}}\right)}}={\frac {\sin 45^{\circ }}{\sin 30^{\circ }}}}$

${\textstyle \therefore A=60^{\circ }}$

Кроме того, изменение угла отклонения при произвольном угле падения можно выразить в одном уравнении, выразив $e$ через $i$ в формуле призмы, используя закон Снеллиуса:

$\delta =i-A+\sin ^{-1}\left(n\cdot \sin \left(A-\sin ^{-1}\left({\frac {\sin i}{n}}\right)\right)\right)=f(i)(say)$

Нахождение минимумов этого уравнения также даст то же соотношение для минимального отклонения, что и выше.

положить $f'(i)=0$ , мы получаем,

${\frac {\cos \left(A-\sin ^{-1}\left({\frac {\sin i}{u}}\right)\right)\cos i}{\sqrt {\left(1-u^{2}\sin ^{2}\left(A-\sin ^{-1}\left({\frac {\sin i}{u}}\right)\right)\right)\left(1-{\frac {\sin ^{2}i}{u^{2}}}\right)}}}=1$ , и решив это уравнение, мы можем получить значение угла падения для определенного значения угла призмы и значение относительного показателя преломления призмы, при котором будет получен минимальный угол отклонения. Уравнение и описание приведены здесь.

Для тонкой призмы

В тонкой или малоугольной призме, когда углы становятся очень маленькими, синус угла почти равен самому углу, и это дает много полезных результатов.

Поскольку $D m$ и $A$ очень малы,

${\begin{aligned}n&\approx {\dfrac {\frac {A+D_{m}}{2}}{\frac {A}{2}}}\\n&={\frac {A+D_{m}}{A}}\\D_{m}&=An-A\end{aligned}}$

$\therefore D_{m}=A(n-1)$ ^[1]^[4]

Использование аналогичного подхода с законом Снелла и формулой призмы для вообще тонкой призмы приводит к тому же самому результату для угла отклонения.

Поскольку $i$ , $e$ и $r$ малы,

$n\approx {\frac {i}{r_{1}}},n\approx {\frac {e}{r_{2}}}$

По формуле призмы ${\begin{aligned}\delta &=nr_{1}+nr_{2}-A\\&=n(r_{1}+r_{2})-A\\&=nA-A\\&=A(n-1)\end{aligned}}$

Таким образом, можно сказать, что тонкая призма всегда находится в минимальном отклонении.

Экспериментальное определение

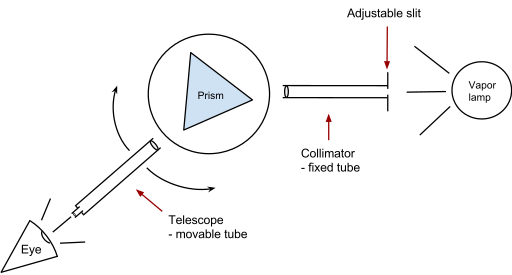
Минимальное отклонение можно найти вручную или с помощью спектрометра. Либо призму удерживают неподвижной и регулируют угол падения, либо призму поворачивают, сохраняя фиксированным источник света. ^[6]^[7]

Минимальный угол рассеивания

Минимальный угол рассеивания белого света — это разница минимального угла отклонения красного и фиолетового лучей светового луча, проходящего через призму. ^[2]

Для тонкой призмы отклонение фиолетового света $\delta _{v}$ является $(n_{v}-1)A$ и красный свет, $\delta _{r}$ является $(n_{r}-1)A$ . Разница в отклонении красного и фиолетового света, $(\delta _{v}-\delta _{r})=(n_{v}-n_{r})A$ называется угловой дисперсией, создаваемой призмой.

Приложения

Проведение радиусов к точкам интерференции показывает, что углы преломления равны, тем самым доказывая минимальное отклонение.

Одним из факторов, вызывающих радугу, является группировка световых лучей под минимальным углом отклонения, близким к углу радуги (42°). ^[3]^[8]

Он также ответственен за такие явления, как ореолы и солнечные лучи , возникающие в результате отклонения солнечного света в мини-призмах шестиугольных кристаллов льда в воздухе, преломляющих свет с минимальным отклонением 22°. ^[3]^[9]

См. также

Ссылки

^ Jump up to: Перейти обратно: ^а ^б ^с ^д «Глава девятая, ЛУЧЕВАЯ ОПТИКА И ОПТИЧЕСКИЕ ПРИБОРЫ». Учебник по физике, часть II для IX класса (PDF) . НЦЭРТ. п. 331.
^ Jump up to: Перейти обратно: ^а ^б ^с «Оптика-Призма» . A. Репетитор по физике уровня
^ Jump up to: Перейти обратно: ^а ^б ^с ^д ^и Марк А. Петерсон. «Минимальное отклонение призмы» . мтолиоке . Колледж Маунт-Холиок . Архивировано из оригинала 23 мая 2019 г.
^ Jump up to: Перейти обратно: ^а ^б «Преломление через призмы» . Школа физики .
^ Jump up to: Перейти обратно: ^а ^б «Призма» . Гиперфизика .
^ «Угол минимального отклонения» . Скрибд .
^ «Экспериментальная установка для измерения угла минимального отклонения призменным спектрометром» . Исследовательские ворота .
^ «Радуга» . www.school Physics.co.uk .
^ «Гало 22°» . Гиперфизика .

Внешние ссылки

Минимальное отклонение, часть 1 и часть 2 в Академии Хана
Преломление через призму в учебнике NCERT
Минимальное отклонение по Prism. Архивировано 23 мая 2019 г. в Wayback Machine Марком Петерсоном, Колледж Маунт-Холиок.

[:1-1] Jump up to: Перейти обратно: ^а ^б ^с ^д «Глава девятая, ЛУЧЕВАЯ ОПТИКА И ОПТИЧЕСКИЕ ПРИБОРЫ». Учебник по физике, часть II для IX класса (PDF) . НЦЭРТ. п. 331.

[:2-2] Jump up to: Перейти обратно: ^а ^б ^с «Оптика-Призма» . A. Репетитор по физике уровня

[:0-3] Jump up to: Перейти обратно: ^а ^б ^с ^д ^и Марк А. Петерсон. «Минимальное отклонение призмы» . мтолиоке . Колледж Маунт-Холиок . Архивировано из оригинала 23 мая 2019 г.

[:3-4] Jump up to: Перейти обратно: ^а ^б «Преломление через призмы» . Школа физики .

[:4-5] Jump up to: Перейти обратно: ^а ^б «Призма» . Гиперфизика .

[6] «Угол минимального отклонения» . Скрибд .

[7] «Экспериментальная установка для измерения угла минимального отклонения призменным спектрометром» . Исследовательские ворота .

[8] «Радуга» . www.school Physics.co.uk .

[9] «Гало 22°» . Гиперфизика .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]