Переписывание графа

В информатике преобразование графов или переписывание графов относится к методу алгоритмического создания нового графа из исходного графа. Он имеет множество применений, начиная от разработки программного обеспечения ( создания программного обеспечения , а также проверки программного обеспечения ) до алгоритмов компоновки и генерации изображений.

Преобразования графов можно использовать в качестве абстракции вычислений. Основная идея заключается в том, что если состояние вычисления можно представить в виде графа, то дальнейшие шаги в этом вычислении можно представить в виде правил преобразования на этом графе. Такие правила состоят из исходного графа, который должен быть сопоставлен с подграфом в завершенном состоянии, и замещающего графа, который заменит совпавший подграф.

Формально система переписывания графов обычно состоит из набора правил переписывания графов вида $L\rightarrow R$, с $L$ называется графом шаблона (или левой частью) и $R$ называется графом замены (или правой частью правила). Правило перезаписи графа применяется к главному графу путем поиска вхождения графа-шаблона ( сопоставление с образцом , таким образом решая проблему изоморфизма подграфа ) и путем замены найденного вхождения экземпляром графа замены. Правила перезаписи можно дополнительно регулировать в случае помеченных графов , например, в грамматиках графов, регулируемых строками.

Иногда грамматика графа используется как синоним системы переписывания графов , особенно в контексте формальных языков ; другая формулировка используется для подчеркивания цели конструкций, таких как перечисление всех графов из некоторого начального графа, т.е. генерация языка графов – вместо простого преобразования данного состояния (основного графа) в новое состояние.

Подходы к переписыванию графов

Вверху: пример правила перезаписи графа ( оптимизация конструкции компилятора: умножение на 2 заменено сложением). Внизу: применение правила для оптимизации «y=x*2» до «y=x+x».

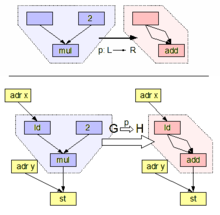
Алгебраический подход

Алгебраический подход к переписыванию графов основан на теории категорий . Алгебраический подход далее делится на подподходы, наиболее распространенными из которых являются подход двойного выталкивания (DPO) и подход одиночного выталкивания (SPO) . Другие подподходы включают подход полуторного выталкивания и метод отката .

С точки зрения подхода DPO правило переписывания графов представляет собой пару морфизмов в категории графов и гомоморфизмов графов между ними: $r=(L\leftarrow K\rightarrow R)$, также написано $L\supseteq K\subseteq R$, где $K\rightarrow L$ является инъективным . Граф K называется инвариантным или иногда графом склейки . Шаг переписывания морфизме или применение правила r к главному графу G определяется двумя диаграммами выталкивания , обе возникающими в одном и том же . $k\colon K\rightarrow D$, где D — контекстный граф (отсюда и название double -pushout). Еще один морфизм графа $m\colon L\rightarrow G$ моделирует появление L в G и называется совпадением . Практическое понимание этого заключается в том, что $L$ это подграф, который соответствует из $G$ (см. проблему изоморфизма подграфов ), и после того, как совпадение найдено, $L$ заменяется на $R$ в графе хоста $G$ где $K$ служит интерфейсом, содержащим узлы и ребра, сохраняющиеся при применении правила. График $K$ необходим для присоединения сопоставляемого шаблона к его контексту: если он пуст, совпадение может обозначать только целый связный компонент графа $G$.

Напротив, правило переписывания графа подхода SPO представляет собой единственный морфизм в категории помеченных мультиграфов и частичных отображений , которые сохраняют структуру мультиграфа: $r\colon L\rightarrow R$. Таким образом, шаг перезаписи определяется одной диаграммой выталкивания . Практическое понимание этого похоже на подход DPO. Разница в том, что между главным графом G и графом G', являющимся результатом этапа перезаписи, нет интерфейса.

С практической точки зрения ключевое различие между DPO и SPO заключается в том, как они справляются с удалением узлов со смежными ребрами, в частности, как они избегают того, чтобы такие удаления могли оставить после себя «висячие ребра». Подход DPO удаляет узел только тогда, когда правило определяет также удаление всех соседних ребер (это условие висячего узла можно проверить на предмет заданного совпадения), тогда как подход SPO просто удаляет соседние ребра, не требуя явного указания.

Существует также другой алгебраический подход к переписыванию графов, основанный главным образом на булевой алгебре и алгебре матриц, называемый грамматиками матричных графов .

Определить переписывание графа

Еще один подход к переписыванию графов, известный как детерминированное переписывание графов, возник из логики и теории баз данных . В этом подходе графы рассматриваются как экземпляры базы данных, а операции перезаписи — как механизм определения запросов и представлений; следовательно, любая перезапись необходима для получения уникальных результатов ( с точностью до изоморфизма ), и это достигается путем одновременного применения любого правила перезаписи по всему графу, где бы оно ни применялось, таким образом, чтобы результат действительно был определен однозначно.

Переписывание графика терминов

Другой подход к переписыванию графов — это переписывание графов терминов , которое включает обработку или преобразование графов терминов (также известных как абстрактные семантические графы ) с помощью набора правил синтаксической перезаписи.

компилятора Графы термов — важная тема в исследованиях языков программирования, поскольку правила переписывания графов термов способны формально выражать операционную семантику . Графы термов также используются в качестве абстрактных машин, способных моделировать химические и биологические вычисления, а также графические вычисления, такие как модели параллелизма. Графы термов могут выполнять автоматическую проверку и логическое программирование, поскольку они хорошо подходят для представления количественных утверждений в логике первого порядка. Программное обеспечение для символьного программирования — это еще одно приложение для графов термов, которые способны представлять и выполнять вычисления с помощью абстрактных алгебраических структур, таких как группы, поля и кольца.

Конференция ТЕРМГРАФ полностью сосредоточен на исследованиях в области переписывания графов терминов и его приложений.

Классы грамматики графов и система переписывания графов

Системы перезаписи графов естественным образом группируются в классы в зависимости от типа используемого представления графов и способа выражения переписывания. Термин «грамматика графа», иначе эквивалентный системе переписывания графов или системе замены графов, чаще всего используется в классификациях. Некоторые распространенные типы:

• Грамматики атрибутивных графов , обычно формализуемые с использованием либо подхода с одним выталкиванием , либо подхода с двойным выталкиванием для описания замен, упомянутых в приведенном выше разделе, посвященном алгебраическому подходу к переписыванию графа.
• Грамматики гиперграфов, включая в качестве более ограничительных подклассов грамматики графов портов , грамматики линейных графов и сети взаимодействия .

Реализации и приложения

Графы — выразительный, наглядный и математически точный формализм моделирования объектов (сущностей), связанных отношениями; объекты представлены узлами, а отношения между ними — ребрами. Узлы и ребра обычно типизируются и атрибутируются. Вычисления в этой модели описываются изменениями отношений между сущностями или изменениями атрибутов элементов графа. Они закодированы в правилах перезаписи/преобразования графов и выполняются системами перезаписи/инструментами преобразования графов.

• Инструменты, нейтральные к предметной области приложения:
  • AGG — грамматическая система атрибутированных графов ( Java ).
  • GP 2 — это визуальный язык графового программирования, основанный на правилах, предназначенный для облегчения формальных рассуждений над графовыми программами.
  • GMTE. Архивировано 13 марта 2018 г. в Wayback Machine , механизме сопоставления и преобразования графов для сопоставления и преобразования графов. Это реализация расширения алгоритма Мессмера с использованием C++ .
  • GrGen.NET — генератор перезаписи графов, инструмент преобразования графов, создающий C# -код или .NET-сборки.
  • GROOVE — набор инструментов на основе Java для редактирования графов и правил преобразования графов, исследования пространств состояний грамматик графов и проверки моделей этих пространств состояний; также может использоваться в качестве механизма преобразования графов.
  • Verigraph — система спецификации и проверки программного обеспечения, основанная на переписывании графов ( Haskell ).
• Инструменты, решающие задачи программной инженерии (в основном MDA ) с переписыванием графов:
  • eMoflon , EMF-совместимый инструмент преобразования моделей с поддержкой моделирования на основе историй и грамматик тройного графа.
  • EmorF. Архивировано 22 апреля 2016 г. на Wayback Machine. Система переписывания графов на основе EMF на месте и от модели к модели , поддерживающая преобразование .
  • Фуджаба использует моделирование на основе историй — язык переписывания графов, основанный на PROGRES.
  • Базы данных графов часто поддерживают динамическое переписывание графов.
  • Большой .
  • Gremlin — язык программирования на основе графов (см. «Переписывание графов »).
  • Henshin — система переписывания графов на основе EMF на месте и от модели к модели , поддерживающая преобразование , критический парный анализ и проверку модели .
  • PROGRES , интегрированная среда и язык очень высокого уровня для систем перезаписи графов PROGRES.
  • ВЕТРЫ .
• Инструменты машиностроения
  • GraphSynth — это интерпретатор и среда пользовательского интерфейса для создания неограниченных графовых грамматик, а также тестирования и поиска результирующего языкового варианта. Он сохраняет графики и правила грамматики графов в виде файлов XML и написан на C# .
  • Soley Studio — интегрированная среда разработки систем преобразования графов. Основное направление его применения — анализ данных в области машиностроения.
• Биологические приложения
  • Функционально-структурное моделирование объекта с помощью языка, основанного на графовой грамматике
  • Моделирование многоклеточного развития с помощью грамматик графов, регулируемых строками
  • Каппа — это основанный на правилах язык для моделирования систем взаимодействующих агентов, в первую очередь основанный на молекулярной системной биологии.
• Искусственный интеллект/обработка естественного языка
  • OpenCog предоставляет базовый инструмент сопоставления шаблонов (на гиперграфах ), который используется для реализации различных алгоритмов искусственного интеллекта.
  • RelEx — англоязычный парсер, который использует перезапись графа для преобразования анализа ссылок в анализ зависимостей .
• Язык компьютерного программирования
  • Язык программирования Clean реализован с помощью переписывания графов.

См. также

• Теория графов
• Грамматика фигур
• Формальная грамматика
• Абстрактное переписывание — обобщение переписывания графов.

Ссылки

Источники

• Розенберг, Гжегож (1997), Справочник по грамматикам графов и вычислениям посредством преобразований графов , том. 1–3, World Scientific Publishing, ISBN.  9810228848 , заархивировано из оригинала 4 октября 2013 г. , получено 11 июля 2012 г.
• Перес, П.П. (2009), Грамматики матричного графа: алгебраический подход к динамике графов , VDM Verlag , ISBN  978-3-639-21255-6 .
• Хекель, Р. (2006). Коротко о преобразовании графа . Электронные заметки по теоретической информатике 148 (1 СПЕЦ. Вып.), стр. 187–198.
• Кениг, Барбара (2004). Анализ и верификация систем с динамически развивающейся структурой . Докторская диссертация, Штутгартский университет. Архивировано 25 июня 2007 г. в Wayback Machine , стр. 65–180.
• Лобо, Дэниел; Вико, Франсиско Дж.; Дассов, Юрген (01 октября 2011 г.). «Грамматики графов с перезаписью, регулируемой строками» . Теоретическая информатика . 412 (43): 6101–6111. дои : 10.1016/j.tcs.2011.07.004 . HDL : 10630/6716 . ISSN   0304-3975 .
• Гжегож Розенберг , изд. (февраль 1997 г.). Фундаменты . Справочник по грамматикам графов и вычислениям путем преобразования графов. Том. 1. Мировая научная. дои : 10.1142/3303 . ISBN  978-981-02-2884-2 .
• Хартмут Эриг ; Грегор Энгельс; Ханс-Йорг Креовски ; Гжегож Розенберг, ред. (октябрь 1999 г.). Приложения, языки и инструменты . Справочник по грамматикам графов и вычислениям путем преобразования графов. Том. 2. Мировая научная. дои : 10.1142/4180 . ISBN  978-981-02-4020-2 .
• Хартмут Эриг; Ханс-Йорг Креовски; Уго Монтанари; Гжегож Розенберг, ред. (август 1999 г.). Параллелизм, параллелизм и распределение . Справочник по грамматикам графов и вычислениям путем преобразования графов. Том. 3. Мировая научная. дои : 10.1142/4181 . ISBN  978-981-02-4021-9 .