Структуры Мичелла

Структуры Мичелла — это структуры, которые являются оптимальными на основе критериев, определенных AGM Мичеллом в его часто цитируемой статье 1904 года.

Мичелл утверждает, что «рама (сегодня называемая фермой) (оптимальна) достигает предела экономии материала, возможного в любой рамной конструкции при одних и тех же приложенных силах, если занимаемое ею пространство может быть подвергнуто соответствующей небольшой деформации, например что деформации во всех стержнях рамы увеличиваются на равные доли их длины, не менее чем на дробное изменение длины любого элемента пространства».

Приведенный выше вывод основан на теореме Максвелла о траектории нагрузки:

$\sum _{}l_{p}f_{p}-\sum _{}l_{q}f_{q}=C$

Где $f_{p}$ — значение натяжения в любом натяжном элементе длины $l_{p}$, $f_{q}$ — значение сжатия в любом элементе сжатия длиной $l_{q}$ и $C$ — это постоянная величина, основанная на внешних нагрузках, приложенных к конструкции.

На основе теоремы Максвелла о пути нагрузки, уменьшающем путь нагрузки растянутых элементов. $\textstyle \sum _{}l_{p}f_{p}$ на ту же величину уменьшит путь нагрузки на компрессионные элементы $\textstyle \sum _{}l_{q}f_{q}$ для заданного набора внешних нагрузок. Конструкцией с минимальным путем нагрузки считается конструкция, имеющая минимальную податливость (имеющая минимальный взвешенный прогиб в точках приложения нагрузок, взвешенный по значениям этих нагрузок). В результате конструкции Michell представляют собой фермы с минимальным соответствием требованиям.

Особые случаи

1. Все стержни фермы испытывают нагрузку одного знака (растяжение или сжатие).

Требуемый объем материала одинаков для всех возможных случаев при заданном наборе нагрузок. Мичелл определяет минимально необходимый объем материала следующим образом: ${\textstyle V_{m}={\frac {\sum _{}lf}{P}}}$

Где $P$ – допустимое напряжение в материале.

2. Смешанные планки растяжения и сжатия.

Более общим случаем являются рамы, состоящие из стержней, которые как до, так и после соответствующей деформации образуют кривые ортогональных систем. Двумерная ортогональная система остается ортогональной после растяжения одной серии кривых и сжатия другой с равной деформацией тогда и только тогда, когда наклон между любыми двумя соседними кривыми одной и той же серии постоянен по всей их длине. Это требование приводит к тому, что перпендикулярная серия кривых должна быть либо:

а) системы касательных и эвольвент или

б) системы пересекающихся логарифмических спиралей .

Обратите внимание, что прямая линия или окружность являются частными случаями логарифмической спирали .

Примеры

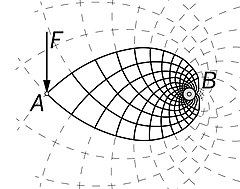
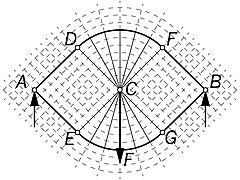
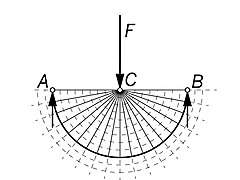
Мичелл привел несколько примеров оптимальных рамок:

а	б	с	д	и
Одна сила F, приложенная к точке А и действующая под прямым углом к ​​линии AB.	Одна сила F, приложенная в точке C, с центром между опорами в точках A и B (решение для всего пространства)	Одна сила F, приложенная в точке C, с центром между опорами в точках A и B (решение в полупространстве)	Балка с центральной нагрузкой, сила которой отклоняется от прямой линии между опорами. Конструкция аналогична примерам б и в.	Равные и противоположные пары приложены в точках А, В на прямой АВ. Минимальный кадр состоит из серии румбических линий, наклоненных под углом 45 градусов к меридианам сферы, имеющим полюса в точках А и В.

Фермы Прагера

В последние годы было проведено множество исследований дискретных оптимальных ферм. Несмотря на то, что фермы Мичелла определяются как континуум (бесконечное число элементов), их также иногда называют фермами Мичелла. Значительный вклад в тему дискретных оптимальных ферм внес Уильям Прагер , который использовал метод круга относительных перемещений, чтобы прийти к оптимальной топологии таких ферм (обычно консольных). В знак признания вклада Прагера дискретные фермы Мичелла иногда называют фермами Прагера. Более поздняя геометрия консольных ферм Прагера была формализована Мазуреком, Бейкером и Тортом. который заметил определенные геометрические соотношения между элементами оптимальных дискретных ферм для трехточечных или трехсиловых задач.