Анализ главных компонентов ядра

В области многомерной статистики анализ главных компонент ядра (kernel PCA) ^[1]является расширением анализа главных компонент (PCA) с использованием методов методов ядра . С помощью ядра первоначально линейные операции PCA выполняются в воспроизводящем ядерном гильбертовом пространстве .

Предыстория: линейный PCA

Напомним, что обычный PCA работает с данными с нулевым центром; то есть,

{\frac {1}{N}}\sum _{i=1}^{N}\mathbf {x} _{i}=\mathbf {0}

,

где $\mathbf {x} _{i}$ является одним из $N$ многомерные наблюдения.Он работает путем диагонализации ковариационной матрицы ,

C={\frac {1}{N}}\sum _{i=1}^{N}\mathbf {x} _{i}\mathbf {x} _{i}^{\top }

другими словами, он дает собственное разложение ковариационной матрицы:

\lambda \mathbf {v} =C\mathbf {v}

который можно переписать как

\lambda \mathbf {x} _{i}^{\top }\mathbf {v} =\mathbf {x} _{i}^{\top }C\mathbf {v} \quad {\textrm {for}}~i=1,\ldots ,N

. ^[2]

(См. также: Ковариационная матрица как линейный оператор )

Введение ядра в PCA

Чтобы понять полезность ядра PCA, особенно для кластеризации, обратите внимание, что, хотя N точек, как правило, не могут быть линейно разделены в $d<N$ измерениях, их почти всегда можно линейно разделить по $d\geq N$ размеры. То есть, учитывая N баллов, $\mathbf {x} _{i}$ , если мы отобразим их в N -мерное пространство с

\Phi (\mathbf {x} _{i})

где

\Phi :\mathbb {R} ^{d}\to \mathbb {R} ^{N}

,

легко построить гиперплоскость , разделяющую точки на произвольные кластеры. Конечно, это $\Phi$ создает линейно независимые векторы, поэтому нет никакой ковариации, по которой можно было бы явно выполнить собственное разложение , как в линейном PCA.

Вместо этого в ядре PCA нетривиальный, произвольный $\Phi$ «выбирается» функция, которая никогда не вычисляется явно, что дает возможность использовать очень многомерные значения. $\Phi$ если нам никогда не придется фактически оценивать данные в этом пространстве. Поскольку мы обычно стараемся избегать работы в $\Phi$ -space, которое мы назовем «пространством функций», мы можем создать ядро N на N.

K=k(\mathbf {x} ,\mathbf {y} )=(\Phi (\mathbf {x} ),\Phi (\mathbf {y} ))=\Phi (\mathbf {x} )^{T}\Phi (\mathbf {y} )

которое представляет собой внутреннее пространство продукта (см. матрицу Грамиана ) трудноразрешимого в противном случае пространства признаков. Двойственная форма, возникающая при создании ядра, позволяет нам математически сформулировать версию PCA, в которой мы фактически никогда не решаем собственные векторы и собственные значения ковариационной матрицы в $\Phi (\mathbf {x} )$ -space (см. трюк с ядром ). N-элементы в каждом столбце K представляют собой скалярное произведение одной точки преобразованных данных относительно всех преобразованных точек (N точек). Некоторые известные ядра показаны в примере ниже.

Поскольку мы никогда не работаем непосредственно в пространстве признаков, формулировка ядра PCA ограничена тем, что она вычисляет не сами основные компоненты, а проекции наших данных на эти компоненты. Чтобы оценить проекцию из точки в пространстве объектов $\Phi (\mathbf {x} )$ на k-ю главную компоненту $V^{k}$ (где верхний индекс k означает компонент k, а не степени k)

{V^{k}}^{T}\Phi (\mathbf {x} )=\left(\sum _{i=1}^{N}\mathbf {a} _{i}^{k}\Phi (\mathbf {x} _{i})\right)^{T}\Phi (\mathbf {x} )

Мы отмечаем, что $\Phi (\mathbf {x} _{i})^{T}\Phi (\mathbf {x} )$ обозначает скалярное произведение, которое представляет собой просто элементы ядра $K$ . Кажется, осталось только вычислить и нормализовать $\mathbf {a} _{i}^{k}$ , что можно сделать, решив уравнение на собственный вектор

N\lambda \mathbf {a} =K\mathbf {a}

где $N$ - количество точек данных в наборе, а $\lambda$ и $\mathbf {a}$ являются собственными значениями и собственными векторами $K$ . Затем для нормализации собственных векторов $\mathbf {a} ^{k}$ , мы требуем этого

1=(V^{k})^{T}V^{k}

Необходимо учитывать тот факт, что независимо от того, $x$ имеет нулевое среднее в исходном пространстве, его центрирование не гарантируется в пространстве признаков (которое мы никогда не вычисляем явно). Поскольку для выполнения эффективного анализа главных компонент необходимы центрированные данные, мы « централизуем » $K$ стать $K'$

K'=K-\mathbf {1_{N}} K-K\mathbf {1_{N}} +\mathbf {1_{N}} K\mathbf {1_{N}}

где $\mathbf {1_{N}}$ обозначает матрицу размера N на N, для которой каждый элемент принимает значение $1/N$ . Мы используем $K'$ для выполнения алгоритма ядра PCA, описанного выше.

Здесь следует проиллюстрировать одно предостережение относительно ядра PCA. В линейном PCA мы можем использовать собственные значения для ранжирования собственных векторов в зависимости от того, какая часть изменений данных захватывается каждым главным компонентом. Это полезно для уменьшения размерности данных, а также может быть применено к KPCA. Однако на практике бывают случаи, когда все варианты данных одинаковы. Обычно это вызвано неправильным выбором масштаба ядра.

Большие наборы данных

На практике большой набор данных приводит к большому K, и хранение K может стать проблемой. Один из способов справиться с этой проблемой — выполнить кластеризацию набора данных и заполнить ядро средствами этих кластеров. Поскольку даже этот метод может дать относительно большое значение K, обычно вычисляются только верхние собственные значения P, а собственные векторы собственных значений вычисляются таким образом.

Пример

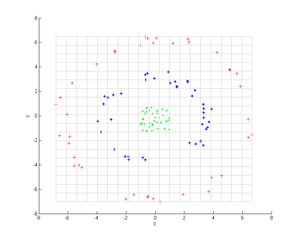
Рассмотрим три концентрических облака точек (показано); мы хотим использовать ядро PCA для идентификации этих групп. Цвет точек не представляет информацию, используемую в алгоритме, а только показывает, как преобразование перемещает точки данных.

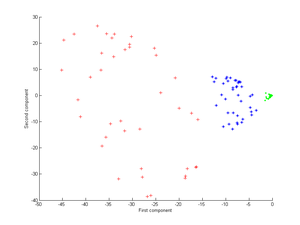
Сначала рассмотрим ядро

k({\boldsymbol {x}},{\boldsymbol {y}})=({\boldsymbol {x}}^{\mathrm {T} }{\boldsymbol {y}}+1)^{2}

Применение этого к PCA ядра дает следующее изображение.

Теперь рассмотрим гауссово ядро:

k({\boldsymbol {x}},{\boldsymbol {y}})=e^{\frac {-||{\boldsymbol {x}}-{\boldsymbol {y}}||^{2}}{2\sigma ^{2}}},

То есть это ядро является мерой близости, равной 1 при совпадении точек и равной 0 на бесконечности.

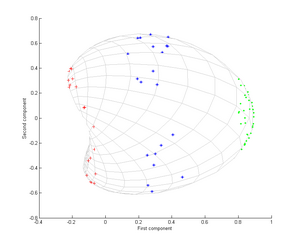
Обратите внимание, в частности, что первого главного компонента достаточно, чтобы различить три разные группы, что невозможно при использовании только линейного PCA, поскольку линейный PCA работает только в заданном (в данном случае двумерном) пространстве, в котором эти концентрические облака точек являются не является линейно разделимым.

Приложения

Было продемонстрировано, что Kernel PCA полезен для обнаружения новинок. ^[3] и шумоподавление изображения. ^[4]

См. также

Ссылки

^ Шёлкопф, Бернхард; Смола, Алекс; Мюллер, Клаус-Роберт (1998). «Анализ нелинейных компонентов как проблема собственных значений ядра». Нейронные вычисления . 10 (5): 1299–1319. CiteSeerX 10.1.1.100.3636 . дои : 10.1162/089976698300017467 . S2CID 6674407 .
^ Шолькопф, Бернхард; Смола, Александр; Мюллер, Клаус-Роберт (декабрь 1996 г.). Нелинейный анализ компонентов как проблема собственных значений ядра (PDF) (Технический отчет). Институт биологической кибернетики Макса Планка. 44.
^ Хоффманн, Хейко (2007). «Ядро PCA для обнаружения новинок» . Распознавание образов . 40 (3): 863–874. Бибкод : 2007PatRe..40..863H . дои : 10.1016/j.patcog.2006.07.009 .
^ PCA ядра и шумоподавление в пространствах функций. НИПС, 1999 г.

[1] Шёлкопф, Бернхард; Смола, Алекс; Мюллер, Клаус-Роберт (1998). «Анализ нелинейных компонентов как проблема собственных значений ядра». Нейронные вычисления . 10 (5): 1299–1319. CiteSeerX 10.1.1.100.3636 . дои : 10.1162/089976698300017467 . S2CID 6674407 .

[2] Шолькопф, Бернхард; Смола, Александр; Мюллер, Клаус-Роберт (декабрь 1996 г.). Нелинейный анализ компонентов как проблема собственных значений ядра (PDF) (Технический отчет). Институт биологической кибернетики Макса Планка. 44.

[3] Хоффманн, Хейко (2007). «Ядро PCA для обнаружения новинок» . Распознавание образов . 40 (3): 863–874. Бибкод : 2007PatRe..40..863H . дои : 10.1016/j.patcog.2006.07.009 .

[4] PCA ядра и шумоподавление в пространствах функций. НИПС, 1999 г.

[1]

[2]

[3]

[4]