Спектральная кластеризация

В многомерной статистике методы спектральной кластеризации используют спектр ( собственные значения ) матрицы сходства данных для уменьшения размерности перед кластеризацией в меньшем количестве измерений. Матрица сходства предоставляется в качестве входных данных и состоит из количественной оценки относительного сходства каждой пары точек в наборе данных.

Применительно к сегментации изображений спектральная кластеризация известна как категоризация объектов на основе сегментации .

Определения

Учитывая нумерованный набор точек данных, матрица подобия может быть определена как симметричная матрица. $A$ , где $A_{ij}\geq 0$ представляет собой меру сходства между точками данных с индексами $i$ и $j$ . Общий подход к спектральной кластеризации заключается в использовании стандартного метода кластеризации (таких методов много, k -means обсуждается ниже ) на соответствующих векторах матрицы Лапласа собственных $A$ . Существует много разных способов определения лапласиана, которые имеют разные математические интерпретации, поэтому кластеризация также будет иметь разные интерпретации. Соответствующими собственными векторами являются те, которые соответствуют нескольким наименьшим собственным значениям лапласиана, за исключением наименьшего собственного значения, которое будет иметь значение 0. Для эффективности вычислений эти собственные векторы часто вычисляются как собственные векторы, соответствующие нескольким наибольшим собственным значениям оператора Лапласа. функция лапласиана.

Матрица Лапласа

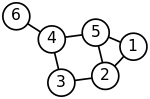
Хорошо известно, что спектральная кластеризация связана с разделением системы масса-пружина, где каждая масса связана с точкой данных, а каждая жесткость пружины соответствует весу края, описывающему сходство двух связанных точек данных, как в пружине. система . В частности, классическая ссылка ^[1] объясняет, что проблема собственных значений, описывающая режимы поперечных колебаний системы масса-пружина, в точности такая же, как проблема собственных значений для графической матрицы Лапласа, определяемой как

L:=D-A

,

где $D$ диагональная матрица

D_{ii}=\sum _{j}A_{ij},

A — матрица смежности .

Массы, плотно связанные пружинами в системе масса-пружина, очевидно, движутся вместе из положения равновесия в низкочастотных режимах вибрации, так что компоненты собственных векторов, соответствующие наименьшим собственным значениям графа Лапласа, можно использовать для осмысленных скопление масс. Например, предполагая, что все пружины и массы идентичны в изображенной двумерной пружинной системе, можно было бы интуитивно ожидать, что наиболее свободные соединенные массы в правой части системы будут двигаться с наибольшей амплитудой и в противоположном направлении. направлению к остальным массам при встряхивании системы — и это ожидание будет подтверждено анализом компонент собственных векторов графа Лапласа, соответствующих наименьшим собственным значениям, т. е. наименьшим частотам колебаний .

Нормализация матрицы Лапласа

Цель нормализации состоит в том, чтобы сделать все диагональные элементы матрицы Лапласа единичными, а также соответствующим образом масштабировать недиагональные элементы. Во взвешенном графе вершина может иметь большую степень из-за малого числа связных ребер, но с большими весами, а также из-за большого количества связных ребер с единичными весами.

Популярным методом нормализованной спектральной кластеризации является алгоритм нормализованных разрезов или алгоритм Ши-Малика, предложенный Цзянбо Ши и Джитендрой Маликом . ^[2] обычно используется для сегментации изображений . Он делит точки на два набора $(B_{1},B_{2})$ на основе собственного вектора $v$ соответствующее второму наименьшему собственному значению симметричного нормализованного лапласиана, определенного как

L^{\text{norm}}:=I-D^{-1/2}AD^{-1/2}.

Вектор $v$ также является собственным вектором , соответствующим второму по величине собственному значению симметрично нормализованной матрицы смежности. $D^{-1/2}AD^{-1/2}.$

Нормированный лапласиан случайного блуждания (или левый) определяется как

L^{\text{rw}}:=D^{-1}L=I-D^{-1}A

а также может использоваться для спектральной кластеризации. Математически эквивалентный алгоритм ^[3] принимает собственный вектор $u$ соответствующее наибольшему собственному значению смежности случайного блуждания нормализованной матрицы $P=D^{-1}A$ .

Собственный вектор $v$ симметрично нормированного лапласиана и собственного вектора $u$ левого нормированного лапласиана связаны тождеством $D^{-1/2}v=u.$

Кластерный анализ с помощью спектрального внедрения

Зная $n$ -к- $k$ матрица $V$ выбранных собственных векторов, отображение — называемое спектральным вложением — исходного $n$ точки данных выполняются для $k$ -мерное векторное пространство с использованием строк $V$ . Теперь анализ сводится к кластеризации векторов с $k$ компонентов, что может быть выполнено различными способами.

В самом простом случае $k=1$ , выбранный единственный собственный вектор $v$ , называемый вектором Фидлера , соответствует второму наименьшему собственному значению. Используя компоненты $v,$ можно разместить все точки, компоненты которых в $v$ положителен в множестве $B_{+}$ и остальное в $B_{-}$ , таким образом разделив график на два раздела и пометив точки данных двумя метками. Этот подход, основанный на знаках, следует интуитивному объяснению спектральной кластеризации с помощью модели массовой пружины - в режиме низкочастотной вибрации, которую вектор Фидлера $v$ представляет собой, точки данных одного кластера, идентифицированные с взаимно сильно связанными массами, будут двигаться вместе в одном направлении, в то время как в дополнительном кластере точки данных, идентифицированные с остальными массами, будут двигаться вместе в противоположном направлении. Алгоритм можно использовать для иерархической кластеризации путем многократного разделения подмножеств одинаковым образом.

В общем случае $k>1$ можно использовать любой метод векторной кластеризации, например DBSCAN .

Алгоритмы

Основной алгоритм

Вычислить лапласиан $L$ (или нормированный лапласиан)
Рассчитаем первый $k$ собственные векторы (собственные векторы, соответствующие $k$ наименьшие собственные значения $L$ )
Рассмотрим матрицу, образованную первым $k$ собственные векторы; тот $l$ -я строка определяет особенности узла графа $l$
Кластеризируйте узлы графа на основе этих функций (например, с помощью кластеризации k-средних ).

Если матрица подобия $A$ еще не было явно построено, эффективность спектральной кластеризации может быть повышена, если решение соответствующей проблемы собственных значений выполняется безматрицным способом ( без явного манипулирования или даже вычисления матрицы подобия), как в алгоритме Ланцоша .

Для графов большого размера второе собственное значение (нормализованной) матрицы Лапласа графа часто плохо обусловлено , что приводит к медленной сходимости итеративных решателей собственных значений. Предварительное обуславливание является ключевой технологией, ускоряющей сходимость, например, в безматричном методе LOBPCG . Спектральная кластеризация успешно применялась к большим графам путем сначала определения структуры их сообществ , а затем кластеризации сообществ. ^[4]

Спектральная кластеризация тесно связана с нелинейным уменьшением размерности , а методы уменьшения размерности, такие как локально-линейное внедрение, могут использоваться для уменьшения ошибок из-за шума или выбросов. ^[5]

Затраты

Обозначая количество точек данных через $n$ , важно оценить объем памяти и время вычислений или количество выполненных арифметических операций (АО) в зависимости от $n$ . Независимо от алгоритма спектральной кластеризации, двумя основными затратными статьями являются построение графа Лапласа и определение его $k$ собственные векторы для спектрального вложения. Последний шаг — определение меток от $n$ -к- $k$ матрица собственных векторов — обычно самый дешевый вариант, требующий только $kn$ АО и создание просто $n$ -к- $1$ вектор меток в памяти.

Необходимость построения графа Лапласа является общей для всех методов кластеризации, основанных на расстоянии или корреляции. Вычисление собственных векторов характерно только для спектральной кластеризации.

Построение графа Лапласа

Граф Лапласа может быть и обычно строится на основе матрицы смежности. Построение может быть выполнено безматрично, т.е. без явного формирования матрицы лапласиана графа и без АО. Это также можно выполнить вместо матрицы смежности без увеличения объема памяти. В любом случае, затраты на построение лапласиана графа по существу определяются затратами на построение графа Лапласа. $n$ -к- $n$ Матрица смежности графов.

Более того, нормированный лапласиан имеет точно такие же собственные векторы, что и нормализованная матрица смежности, но с обратным порядком собственных значений. Таким образом, вместо вычисления собственных векторов, соответствующих наименьшим собственным значениям нормализованного лапласиана, можно эквивалентным образом вычислить собственные векторы, соответствующие наибольшим собственным значениям нормализованной матрицы смежности, даже не говоря о матрице Лапласа.

графа Наивные конструкции матрицы смежности , например, с использованием ядра RBF, делают ее плотной, требуя таким образом $n^{2}$ память и $n^{2}$ АО для определения каждого из $n^{2}$ записи матрицы. Метод Нистрома ^[6] может использоваться для аппроксимации матрицы подобия, но приближенная матрица не является поэлементно положительной, ^[7] т.е. не может быть интерпретировано как сходство, основанное на расстоянии.

Алгоритмы построения матрицы смежности графа в виде разреженной матрицы обычно основаны на поиске ближайшего соседа , который оценивает или выбирает окрестность заданной точки данных для ближайших соседей и вычисляет ненулевые элементы матрицы смежности путем сравнения только пар соседи. Таким образом, количество выбранных ближайших соседей определяет количество ненулевых записей и часто фиксируется так, чтобы объем памяти, занимаемой $n$ -к- $n$ матрица смежности графа - это только $O(n)$ , только $O(n)$ необходимы последовательные арифметические операции для вычисления $O(n)$ ненулевые записи, и вычисления можно тривиально выполнять параллельно.

Вычисление собственных векторов

Стоимость расчета $n$ -к- $k$ (с $k\ll n$ ) матрица выбранных собственных векторов лапласиана графа обычно пропорциональна стоимости умножения $n$ -к- $n$ граф матрица Лапласа с помощью вектора, который сильно зависит от того, является ли матрица Лапласа графа плотной или разреженной. Таким образом, для плотного случая стоимость равна $O(n^{2})$ . Очень часто упоминаемая в литературе стоимость $O(n^{3})$ происходит от выбора $k=n$ и явно вводит в заблуждение, поскольку, например, при иерархической спектральной кластеризации $k=1$ как определяется вектором Фидлера .

В редком случае $n$ -к- $n$ графическая матрица Лапласа с $O(n)$ ненулевые записи, стоимость произведения матрицы-вектора и, следовательно, вычисления $n$ -к- $k$ с $k\ll n$ матрица выбранных собственных векторов равна $O(n)$ , с объемом памяти тоже только $O(n)$ — оба являются оптимальными нижними границами сложности кластеризации $n$ точки данных. Более того, безматричные решатели собственных значений, такие как LOBPCG, могут эффективно работать параллельно, например, на нескольких графических процессорах с распределенной памятью, что приводит не только к созданию кластеров высокого качества, которыми славится спектральная кластеризация, но и к максимальной производительности. ^[8]

Программное обеспечение

Бесплатное программное обеспечение, реализующее спектральную кластеризацию, доступно в крупных проектах с открытым исходным кодом, таких как scikit-learn. ^[9] используя ЛОБПКГ ^[10] с многосеточной предварительной обработкой ^[11] ^[12] или ARPACK , MLlib для кластеризации псевдособственных векторов с использованием метода степенной итерации , ^[13] и Р. ^[14]

Связь с другими методами кластеризации

Идеи, лежащие в основе спектральной кластеризации, могут быть не сразу очевидны. Может быть полезно выделить связи с другими методами. В частности, его можно описать в контексте методов кластеризации ядра, что обнаруживает некоторые сходства с другими подходами. ^[15]

Связь с k -средними

с взвешенным ядром k -средних Проблема ^[16]разделяет целевую функцию с задачей спектральной кластеризации, которую можно оптимизировать непосредственно с помощью многоуровневых методов. ^[17]

Связь с DBSCAN

В тривиальном случае определения компонентов связного графа — оптимальных кластеров без разрезанных ребер — спектральная кластеризация также связана со спектральной версией кластеризации DBSCAN , которая находит компоненты, связанные по плотности. ^[18]

Меры по сравнению кластеризации

Рави Каннан, Сантош Вемпала и Адриан Ветта ^[19] предложил меру бикритериев для определения качества данной кластеризации. Они говорили, что кластеризация является (α, ε)-кластеризацией, если проводимость каждого кластера (в кластере) была не менее α, а вес межкластерных ребер составлял не более ε доли от общего веса всех кластеров. ребра в графе. В одной статье они также рассматривают два алгоритма аппроксимации.

История и сопутствующая литература

Спектральная кластеризация имеет долгую историю. ^[20]^[21]^[22]^[23]^[24]^[2]^[25] Спектральная кластеризация как метод машинного обучения была популяризирована Ши и Маликом. ^[2] и Нг, Джордан и Вайс. ^[25]

Идеи и сетевые меры, связанные со спектральной кластеризацией, также играют важную роль в ряде приложений, очевидно, отличных от задач кластеризации. Например, сетям с более сильным спектральным разделением требуется больше времени, чтобы сходиться в моделях обновления общественного мнения, используемых в социологии и экономике. ^[26]^[27]

См. также

Ссылки

^ Деммель, Дж. «CS267: Примечания к лекции 23, 9 апреля 1999 г., Разделение графов, Часть 2» .
^ Jump up to: Перейти обратно: ^а ^б ^с Цзянбо Ши и Джитендра Малик, «Нормализованные разрезы и сегментация изображений» , Транзакции IEEE на PAMI, Vol. 22, № 8, август 2000 г.
^ Марина Мейлэ и Цзянбо Ши, « Сегментация обучения путем случайных блужданий », Нейронные системы обработки информации 13 (NIPS 2000), 2001, стр. 873–879.
^ Заре, Хабиль; Шуштари, П.; Гупта, А.; Бринкман, Р. (2010). «Сокращение данных для спектральной кластеризации для анализа данных высокопроизводительной проточной цитометрии» . БМК Биоинформатика . 11 : 403. дои : 10.1186/1471-2105-11-403 . ПМЦ 2923634 . ПМИД 20667133 .
^ Ариас-Кастро, Э.; Чен, Г.; Лерман, Г. (2011), «Спектральная кластеризация на основе локальных линейных аппроксимаций», Электронный статистический журнал , 5 : 1537–87, arXiv : 1001.1323 , doi : 10.1214/11-ejs651 , S2CID 88518155
^ Фаулкс, К. (2004). «Спектральная группировка по методу Нистрома» . Транзакции IEEE по анализу шаблонов и машинному интеллекту . 26 (2): 214–25. дои : 10.1109/TPAMI.2004.1262185 . ПМИД 15376896 . S2CID 2384316 .
^ Ван, С.; Гиттенс, А.; Махони, MW (2019). «Масштабируемая кластеризация K-средних в ядре с приближением Нистрома: границы относительной ошибки». Журнал исследований машинного обучения . 20 : 1–49. arXiv : 1706.02803 .
^ Асер, Сехер; Боман, Эрик Г.; Глуса, Кристиан А.; Раджаманикам, Сивасанкаран (2021 г.). «Sphynx: параллельный разделитель графов с несколькими графическими процессорами для систем с распределенной памятью». Параллельные вычисления . 106 : 102769. arXiv : 2105.00578 . дои : 10.1016/j.parco.2021.102769 . S2CID 233481603 .
^ «2.3. Кластеризация» .
^ Князев, Андрей Васильевич (2003). Боли; Диллон; Гоша; Коган (ред.). Современные предварительно подготовленные собственные решатели для спектральной сегментации изображений и деления графа пополам . Кластеризация больших наборов данных; Третья Международная конференция IEEE по интеллектуальному анализу данных (ICDM 2003) Мельбурн, Флорида: Компьютерное общество IEEE. стр. 59–62.
^ Князев, Андрей В. (2006). Многомасштабная сегментация спектрального изображения. Многомасштабная предварительная подготовка для вычисления собственных значений лапласианов графа при сегментации изображений . Семинар по быстрому изучению многообразий, В.М. Вильямбург, Вирджиния. дои : 10.13140/RG.2.2.35280.02565 .
^ Князев, Андрей В. (2006). Многомасштабное разбиение спектрального графа и сегментация изображений . Семинар по алгоритмам обработки современных массивных наборов данных Стэнфордского университета и Yahoo! Исследовать.
^ «Кластеризация — API на основе RDD — Документация Spark 3.2.0» .
^ «Кернлаб: лаборатория машинного обучения на основе ядра» . 12 ноября 2019 г.
^ Филиппоне, М.; Камастра, Ф.; Масулли, Ф.; Роветта, С. (январь 2008 г.). «Обзор ядерных и спектральных методов кластеризации» (PDF) . Распознавание образов . 41 (1): 176–190. Бибкод : 2008PatRe..41..176F . дои : 10.1016/j.patcog.2007.05.018 .
^ Диллон, Исландия; Гуань, Ю.; Кулис, Б. (2004). «Ядро k -средних: спектральная кластеризация и нормализованные разрезы» (PDF) . Материалы десятой международной конференции ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных . стр. 551–6.
^ Диллон, Индерджит; Гуань, Юцян; Кулис, Брайан (ноябрь 2007 г.). «Взвешенные разрезы графа без собственных векторов: многоуровневый подход». Транзакции IEEE по анализу шаблонов и машинному интеллекту . 29 (11): 1944–1957. CiteSeerX 10.1.1.131.2635 . дои : 10.1109/tpami.2007.1115 . ПМИД 17848776 . S2CID 9402790 .
^ Шуберт, Эрих; Гесс, Сибилла; Морик, Катарина (2018). Связь DBSCAN с матричной факторизацией и спектральной кластеризацией (PDF) . ЛВДА. стр. 330–334.
^ Каннан, Рави; Вемпала, Сантош; Ветта, Адриан (2004). «О кластеризациях: хорошо, плохо и спектрально». Журнал АКМ . 51 (3): 497–515. дои : 10.1145/990308.990313 . S2CID 207558562 .
^ Чигер, Джефф (1969). «Нижняя оценка наименьшего собственного значения лапласиана». Материалы Принстонской конференции в честь профессора С. Бохнера .
^ Донат, Уильям; Хоффман, Алан (1972). «Алгоритмы разбиения графов и компьютерная логика на основе собственных векторов матриц связей». Бюллетень технической информации IBM .
^ Фидлер, Мирослав (1973). «Алгебраическая связность графов» . Чехословацкий математический журнал . 23 (2): 298–305. дои : 10.21136/CMJ.1973.101168 .
^ Гваттери, Стивен; Миллер, Гэри Л. (1995). «О работоспособности методов разделения спектральных графов». Ежегодный симпозиум ACM-SIAM по дискретным алгоритмам .
^ Дэниел А. Спилман и Шан-Хуа Тэн (1996). «Работы по спектральному разбиению: плоские графы и сетки конечных элементов». Ежегодный симпозиум IEEE по основам информатики .
^ Jump up to: Перейти обратно: ^а ^б Нг, Эндрю Ю.; Джордан, Майкл И.; Вайс, Яир (2002). «О спектральной кластеризации: анализ и алгоритм» (PDF) . Достижения в области нейронных систем обработки информации .
^ ДеМарзо, премьер-министр; Ваянос, Д.; Цвибель, Дж. (1 августа 2003 г.). «Предвзятость убеждения, социальное влияние и одномерные мнения» . Ежеквартальный экономический журнал . 118 (3). Издательство Оксфордского университета: 909–968. дои : 10.1162/00335530360698469 . ISSN 0033-5533 .
^ Голуб, Бенджамин; Джексон, Мэтью О. (26 июля 2012 г.). «Как гомофилия влияет на скорость обучения и динамику наилучшего ответа». Ежеквартальный экономический журнал . 127 (3). Издательство Оксфордского университета (OUP): 1287–1338. дои : 10.1093/qje/qjs021 . ISSN 0033-5533 .

[1] Деммель, Дж. «CS267: Примечания к лекции 23, 9 апреля 1999 г., Разделение графов, Часть 2» .

[:0-2] Jump up to: Перейти обратно: ^а ^б ^с Цзянбо Ши и Джитендра Малик, «Нормализованные разрезы и сегментация изображений» , Транзакции IEEE на PAMI, Vol. 22, № 8, август 2000 г.

[3] Марина Мейлэ и Цзянбо Ши, « Сегментация обучения путем случайных блужданий », Нейронные системы обработки информации 13 (NIPS 2000), 2001, стр. 873–879.

[4] Заре, Хабиль; Шуштари, П.; Гупта, А.; Бринкман, Р. (2010). «Сокращение данных для спектральной кластеризации для анализа данных высокопроизводительной проточной цитометрии» . БМК Биоинформатика . 11 : 403. дои : 10.1186/1471-2105-11-403 . ПМЦ 2923634 . ПМИД 20667133 .

[5] Ариас-Кастро, Э.; Чен, Г.; Лерман, Г. (2011), «Спектральная кластеризация на основе локальных линейных аппроксимаций», Электронный статистический журнал , 5 : 1537–87, arXiv : 1001.1323 , doi : 10.1214/11-ejs651 , S2CID 88518155

[6] Фаулкс, К. (2004). «Спектральная группировка по методу Нистрома» . Транзакции IEEE по анализу шаблонов и машинному интеллекту . 26 (2): 214–25. дои : 10.1109/TPAMI.2004.1262185 . ПМИД 15376896 . S2CID 2384316 .

[7] Ван, С.; Гиттенс, А.; Махони, MW (2019). «Масштабируемая кластеризация K-средних в ядре с приближением Нистрома: границы относительной ошибки». Журнал исследований машинного обучения . 20 : 1–49. arXiv : 1706.02803 .

[msw2014-8] Асер, Сехер; Боман, Эрик Г.; Глуса, Кристиан А.; Раджаманикам, Сивасанкаран (2021 г.). «Sphynx: параллельный разделитель графов с несколькими графическими процессорами для систем с распределенной памятью». Параллельные вычисления . 106 : 102769. arXiv : 2105.00578 . дои : 10.1016/j.parco.2021.102769 . S2CID 233481603 .

[9] «2.3. Кластеризация» .

[10] Князев, Андрей Васильевич (2003). Боли; Диллон; Гоша; Коган (ред.). Современные предварительно подготовленные собственные решатели для спектральной сегментации изображений и деления графа пополам . Кластеризация больших наборов данных; Третья Международная конференция IEEE по интеллектуальному анализу данных (ICDM 2003) Мельбурн, Флорида: Компьютерное общество IEEE. стр. 59–62.

[spectralmultigrid2006-11] Князев, Андрей В. (2006). Многомасштабная сегментация спектрального изображения. Многомасштабная предварительная подготовка для вычисления собственных значений лапласианов графа при сегментации изображений . Семинар по быстрому изучению многообразий, В.М. Вильямбург, Вирджиния. дои : 10.13140/RG.2.2.35280.02565 .

[12] Князев, Андрей В. (2006). Многомасштабное разбиение спектрального графа и сегментация изображений . Семинар по алгоритмам обработки современных массивных наборов данных Стэнфордского университета и Yahoo! Исследовать.

[13] «Кластеризация — API на основе RDD — Документация Spark 3.2.0» .

[14] «Кернлаб: лаборатория машинного обучения на основе ядра» . 12 ноября 2019 г.

[filippone2008survey-15] Филиппоне, М.; Камастра, Ф.; Масулли, Ф.; Роветта, С. (январь 2008 г.). «Обзор ядерных и спектральных методов кластеризации» (PDF) . Распознавание образов . 41 (1): 176–190. Бибкод : 2008PatRe..41..176F . дои : 10.1016/j.patcog.2007.05.018 .

[dhillon2004kernel-16] Диллон, Исландия; Гуань, Ю.; Кулис, Б. (2004). «Ядро k -средних: спектральная кластеризация и нормализованные разрезы» (PDF) . Материалы десятой международной конференции ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных . стр. 551–6.

[17] Диллон, Индерджит; Гуань, Юцян; Кулис, Брайан (ноябрь 2007 г.). «Взвешенные разрезы графа без собственных векторов: многоуровневый подход». Транзакции IEEE по анализу шаблонов и машинному интеллекту . 29 (11): 1944–1957. CiteSeerX 10.1.1.131.2635 . дои : 10.1109/tpami.2007.1115 . ПМИД 17848776 . S2CID 9402790 .

[18] Шуберт, Эрих; Гесс, Сибилла; Морик, Катарина (2018). Связь DBSCAN с матричной факторизацией и спектральной кластеризацией (PDF) . ЛВДА. стр. 330–334.

[19] Каннан, Рави; Вемпала, Сантош; Ветта, Адриан (2004). «О кластеризациях: хорошо, плохо и спектрально». Журнал АКМ . 51 (3): 497–515. дои : 10.1145/990308.990313 . S2CID 207558562 .

[20] Чигер, Джефф (1969). «Нижняя оценка наименьшего собственного значения лапласиана». Материалы Принстонской конференции в честь профессора С. Бохнера .

[21] Донат, Уильям; Хоффман, Алан (1972). «Алгоритмы разбиения графов и компьютерная логика на основе собственных векторов матриц связей». Бюллетень технической информации IBM .

[22] Фидлер, Мирослав (1973). «Алгебраическая связность графов» . Чехословацкий математический журнал . 23 (2): 298–305. дои : 10.21136/CMJ.1973.101168 .

[23] Гваттери, Стивен; Миллер, Гэри Л. (1995). «О работоспособности методов разделения спектральных графов». Ежегодный симпозиум ACM-SIAM по дискретным алгоритмам .

[24] Дэниел А. Спилман и Шан-Хуа Тэн (1996). «Работы по спектральному разбиению: плоские графы и сетки конечных элементов». Ежегодный симпозиум IEEE по основам информатики .

[:1-25] Jump up to: Перейти обратно: ^а ^б Нг, Эндрю Ю.; Джордан, Майкл И.; Вайс, Яир (2002). «О спектральной кластеризации: анализ и алгоритм» (PDF) . Достижения в области нейронных систем обработки информации .

[DeMarzo_Vayanos_Zwiebel_pp._909–968-26] ДеМарзо, премьер-министр; Ваянос, Д.; Цвибель, Дж. (1 августа 2003 г.). «Предвзятость убеждения, социальное влияние и одномерные мнения» . Ежеквартальный экономический журнал . 118 (3). Издательство Оксфордского университета: 909–968. дои : 10.1162/00335530360698469 . ISSN 0033-5533 .

[Golub_Jackson_pp._1287–1338-27] Голуб, Бенджамин; Джексон, Мэтью О. (26 июля 2012 г.). «Как гомофилия влияет на скорость обучения и динамику наилучшего ответа». Ежеквартальный экономический журнал . 127 (3). Издательство Оксфордского университета (OUP): 1287–1338. дои : 10.1093/qje/qjs021 . ISSN 0033-5533 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]