Обратное распространение ошибки во времени

«БПТТ» перенаправляется сюда. Информацию о беговых соревнованиях, первоначально известных как гонка на время в Буши-парке, см. в parkrun .

Обратное распространение ошибки во времени (BPTT) — это метод, основанный на градиенте , для обучения определенных типов рекуррентных нейронных сетей . Его можно использовать для обучения сетей Элмана . Алгоритм был независимо разработан многочисленными исследователями.

Алгоритм

BPTT разворачивает рекуррентную нейронную сеть во времени.

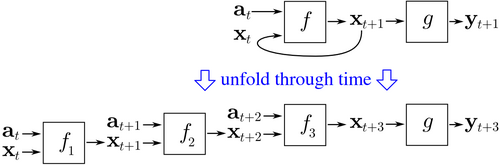
Данные обучения рекуррентной нейронной сети представляют собой упорядоченную последовательность $k$ пары ввода-вывода, $\langle \mathbf {a} _{0},\mathbf {y} _{0}\rangle ,\langle \mathbf {a} _{1},\mathbf {y} _{1}\rangle ,\langle \mathbf {a} _{2},\mathbf {y} _{2}\rangle ,...,\langle \mathbf {a} _{k-1},\mathbf {y} _{k-1}\rangle$. Для скрытого состояния необходимо указать начальное значение. $\mathbf {x} _{0}$. Обычно для этой цели используется вектор, состоящий из всех нулей.

BPTT начинается с развертывания рекуррентной нейронной сети во времени. Развернутая сеть содержит $k$ входы и выходы, но каждая копия сети имеет одни и те же параметры. Затем алгоритм обратного распространения ошибки используется для нахождения градиента стоимости по всем параметрам сети.

Рассмотрим пример нейронной сети, содержащей рекуррентный слой. $f$ и прямой связи слой $g$. Существуют разные способы определения стоимости обучения, но совокупная стоимость всегда представляет собой среднее значение затрат каждого временного шага. Стоимость каждого временного шага может быть рассчитана отдельно. На рисунке выше показано, как стоимость за раз $t+3$ можно вычислить, развернув рекуррентный слой $f$ для трех временных шагов и добавления слоя прямой связи $g$. Каждый экземпляр $f$ в развернутой сети имеют те же параметры. Таким образом, вес обновляется в каждом экземпляре ( $f_{1},f_{2},f_{3}$) суммируются.

Псевдокод

Псевдокод для усеченной версии BPTT, где обучающие данные содержат $n$ пары ввода-вывода, но сеть развернута для $k$ временные шаги:

Back_Propagation_Through_Time(a, y)   // a[t] is the input at time t. y[t] is the output
    Unfold the network to contain k instances of f
    do until stopping criterion is met:
        x := the zero-magnitude vector // x is the current context
        for t from 0 to n − k do      // t is time. n is the length of the training sequence
            Set the network inputs to x, a[t], a[t+1], ..., a[t+k−1]
            p := forward-propagate the inputs over the whole unfolded network
            e := y[t+k] − p;           // error = target − prediction
            Back-propagate the error, e, back across the whole unfolded network
            Sum the weight changes in the k instances of f together.
            Update all the weights in f and g.
            x := f(x, a[t]);           // compute the context for the next time-step

Преимущества

BPTT имеет тенденцию быть значительно быстрее при обучении рекуррентных нейронных сетей, чем методы оптимизации общего назначения, такие как эволюционная оптимизация.

Недостатки

У BPTT есть трудности с локальными оптимумами. В рекуррентных нейронных сетях локальные оптимумы представляют собой гораздо более серьезную проблему, чем в нейронных сетях прямого распространения. Рекуррентная обратная связь в таких сетях имеет тенденцию создавать хаотичные реакции на поверхности ошибок, что приводит к частому возникновению локальных оптимумов и в неудачных местах на поверхности ошибок.

См. также

• Обратное распространение ошибки через структуру