Загадка проливания воды

Загадки с наливанием воды (также называемые задачами с кувшинами для воды , задачами со сцеживанием , ^[1]^[2] головоломки с измерением или головоломки «Крепкий орешек с местью» ) — класс головоломок , включающий конечный набор кувшинов с водой известной целочисленной вместимости (в терминах меры жидкости , такой как литры или галлоны ).Первоначально каждый кувшин содержит известный целый объем жидкости, не обязательно равный его вместимости.

Загадки этого типа спрашивают, сколько шагов переливания воды из одного кувшина в другой (пока один кувшин не станет пустым, а другой не наполнится) необходимо для достижения целевого состояния, определяемого объемом жидкости, которая должна присутствовать в какой-нибудь кувшин или кувшины. ^[3]

Согласно тождеству Безу , такие головоломки имеют решение тогда и только тогда, когда искомый объем кратен наибольшему общему делителю всех целочисленных объемов кувшинов.

Правила

В рамках этих головоломок высказывается распространенное предположение, что кувшины в головоломке имеют неправильную форму и не имеют опознавательных знаков, поэтому невозможно точно измерить любое количество воды, которое не наполняет кувшин полностью. Другие предположения об этих проблемах могут включать в себя то, что вода не может быть пролита и что на каждом этапе выливание воды из источникакувшин в пункт назначения останавливается, когда либо исходный кувшин пуст, либо кувшин назначения полон, в зависимости от того, что произойдет раньше.

Стандартный пример

Стандартный пазл такого типа работает с тремя кувшинами емкостью 8, 5 и 3 литра. Изначально они заправлены объемом 8, 0 и 0 литров. В целевом состоянии они должны быть заполнены 4, 4 и 0 литрами. Загадку можно решить за семь шагов, пройдя через следующую последовательность состояний (обозначаемую тройкой в квадратных скобках трех объемов воды в трех кувшинах):

[8,0,0] → [3,5,0] → [3,2,3] → [6,2,0] → [6,0,2] → [1,5,2] → [1,4,3] → [4,4,0].

Коули (1926) пишет, что эта конкретная головоломка «возродилась еще в средневековье», и отмечает ее появление в учебнике математики Баше 17-го века.

Обратимость действий

Поскольку правила допускают остановку/поворот только на границах декартовой сетки (т.е. при полной мощности каждого кувшина), единственными обратимыми действиями (обратимыми за один шаг) являются:

Переливание воды из полного кувшина в любой кувшин
Переливание воды из любого кувшина в пустой кувшин

Единственные необратимые действия, которые нельзя отменить за один шаг:

Перекачивание воды из частично полного кувшина в другой частично полный кувшин

Ограничиваясь только обратимыми действиями, мы можем построить решение проблемы из желаемого результата. Из пункта [4,4,0] существует только два обратимых действия: Перелить 3 литра из 8-литрового кувшина в пустой 3-литровый кувшин [1,4,3], или перелить 3 литра из 5-литрового кувшина в пустой 3-х литровый кувшин [4,1,3]. Поэтому есть только два решения этой проблемы:

[4,4,0] ↔ [1,4,3] ↔ [1,5,2] ↔ [6,0,2] ↔ [6,2,0] ↔ [3,2,3] ↔ [3,5,0] ↔ [8,0,0]

[4,4,0] ↔ [4,1,3] ↔ [7,1,0] ↔ [7,0,1] ↔ [2,5,1] ↔ [2,3,3] ↔ [5,3,0] ↔ [5,0,3] ↔ [8,0,0]

Вариант с кранами и раковинами

Решение головоломки с кувшинами на 3 и 5 л, краном и сливом.

Правила иногда формулируются путем добавления крана (источника «кувшина» с бесконечной водой) и раковины (сливного «кувшина», принимающего любое количество воды без ограничений). Наполнение кувшина до краёв из-под крана или выливание всего содержимого кувшина в канализацию – каждый шаг при решении проблемы считается одним шагом. Эта версия головоломки была показана в сцене фильма 1995 года « Крепкий орешек с местью» . ^[4] Этот вариант имеет оптимальное решение, которое можно получить с помощью барицентрического графика бильярдной формы (или математического биллиарда). ^[5]

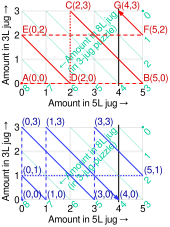
На графике показаны два способа получения 4 литров с использованием 3-литровых и 5-литровых кувшинов, а также источник и сток воды на декартовой сетке с диагональными линиями наклона -1 (такими, что $x+y=const.$ на этих диагональных линиях, обозначающих переливание воды из одного кувшина в другой). Оси x и y представляют количество в кувшинах емкостью 5 и 3 л соответственно. Начиная с (0, 0), обходим сетку по отрезкам линии, поворачиваясь только на ее границах, пока не дойдем до черной линии, обозначающей 4 л в кувшине емкостью 5 л. Сплошные линии обозначают переливание между кувшинами, пунктирные линии — наполнение кувшина, пунктирные линии — опорожнение кувшина.

Объединение любого решения, обход линии 4 L и обращение другого решения возвращается к (0, 0), давая граф цикла . Если и только если объемы кувшинов взаимно просты , посещается каждая граничная точка, что дает алгоритм для измерения любого целого числа вплоть до суммы объемов.

Как было показано в предыдущем разделе, мы можем построить решение проблемы на основе желаемого результата, используя только обратимые действия (опорожнение полного кувшина в раковину и наполнение пустого кувшина из-под крана обратимы). Чтобы получить 4 литра, используя 3-литровые и 5-литровые кувшины, нам нужно достичь точки (4, 0). С точки (4, 0) есть только два обратимых действия: наполнить пустой 3-литровый кувшин до полного из-под крана (4,3), либо перелить 1 л воды из 5-литрового кувшина в 3-литровый. литровый кувшин (1,3). Поэтому есть только два решения проблемы:

(4, 0) ↔ (4, 3) ↔ (5, 2) ↔ (0, 2) ↔ (2, 0) ↔ (2, 3) ↔ (5, 0) ↔ (0, 0)

(4, 0) ↔ (1, 3) ↔ (1, 0) ↔ (0, 1) ↔ (5, 1) ↔ (3, 3) ↔ (3, 0) ↔ (0, 3) ↔ (0, 0)

Граф цикла можно представить упорядоченными парами, соединенными обратимыми действиями:

(0, 0) ↔ (5, 0) ↔ (2, 3) ↔ (2, 0) ↔ (0, 2) ↔ (5, 2) ↔ (4, 3) ↔ (4, 0) ↔ (1, 3) ↔ (1, 0) ↔ (0, 1) ↔ (5, 1) ↔ (3, 3) ↔ (3, 0) ↔ (0, 3) ↔ (0, 0)

который содержит все возможные состояния, достижимые с помощью 3-литрового кувшина и 5-литрового кувшина. Состояния (1, 2), например, невозможно достичь из начального состояния (0, 0), так как в (1, 2) оба кувшина частично заполнены, и никакое обратимое действие из этого состояния невозможно.

Кувшин с исходной водой

Другой вариант ^[6] это когда в одном из кувшинов изначально есть известный объем воды; В этом случае достижимые объемы либо кратны наибольшему общему делителю между двумя контейнерами от существующего известного объема, либо равны нулю. Например, если один кувшин, вмещающий 8 литров, пуст, а в другом кувшине, вмещающем 12 литров, изначально находится 9 литров воды, то с источником (кран) и сливом (раковина) эти два кувшина могут измерять объемами 9 литров, 5 литров, 1 литр, а также 12 литров, 8 литров, 4 литра и 0 литров. Самое простое решение для 5 литров: (9,0) → (9,8) → (12,5); Самое простое решение для 4 литров: (9,0) → (12,0) → (4,8). Эти решения можно визуализировать красными и синими стрелками в декартовой сетке с диагональными линиями (с наклоном -1, такими что $x+y=const.$ на этих диагональных линиях) на расстоянии 4 литров друг от друга как по горизонтали, так и по вертикали.

Опять же, если ограничиться только обратимыми действиями, из нужной точки (5,0) обратимых действий всего два: перелить 5 литров воды из 12-литрового кувшина в 8-литровый кувшин (0,5) , или наполнив пустой 8-литровый кувшин до отказа из-под крана (5,8). Поэтому есть только два решения проблемы:

(5, 0) ↔ (0, 5) ↔ (12, 5) ↔ (9, 8) ↔ (9, 0)

(5, 0) ↔ (5, 8) ↔ (12, 1) ↔ (0, 1) ↔ (1, 0) ↔ (1, 8) ↔ (9, 0)

По вопросу о 4 литрах, т.к. $4\equiv 0\!\mod \!4$ , в начале решения необходимо одно необратимое действие; Это может быть просто вылить все 9 литров воды из 12-литрового кувшина в раковину (0,0) или полностью заполнить ее до 12 литров из-под крана (12,0). Затем мы можем построить наши решения в обратном порядке, как и раньше:

(4, 0) ↔ (4, 8) ↔ (12, 0) ← (9, 0)

(4, 0) ↔ (0, 4) ↔ (12, 4) ↔ (8, 8) ↔ (8, 0) ↔ (0, 8) ↔ (0, 0) ← (9, 0)

Решение для трех кувшинов с использованием барицентрического графика

Если количество кувшинов равно трем, состояние наполнения после каждого шага можно описать диаграммой барицентрических координат , поскольку сумма всех трех целых чисел остается одинаковой на всех этапах. ^[7] В результате шаги можно визуализировать как бильярдные ходы в (обрезанной) системе координат на треугольной решетке.

Барицентрический график справа дает два решения загадки 8, 5 и 3 л. Желтая область обозначает комбинации, достижимые с помощью кувшинов. Начиная с квадрата, сплошные красные и пунктирные синие пути обозначают плавные переходы. Когда вершина попадает в пунктирный черный треугольник, измерено 4 L. При повторном наливании алмаза получается по 4 л в кувшины емкостью 8 и 5 л.

Синий путь на один шаг короче, чем путь для головоломки с двумя кувшинами с краном и сливом, поскольку мы можем накопить 4 л в кувшине на 8 л, чего нет в варианте с двумя кувшинами.

См. также

Головоломка со сжиганием веревки , еще один класс головоломок, включающий комбинацию измерений.
Эффект настройки

Литература

Коули, Элизабет Б. (1926). «Заметка о линейном диофантовом уравнении». Вопросы и обсуждения. Американский математический ежемесячник . 33 (7): 379–381. дои : 10.2307/2298647 . JSTOR 2298647 . МР 1520987 .
Твиди, MCK (1939). «Графический метод решения измерительных задач Тарталья». Математический вестник . Том. 23, нет. 255. С. 278–282. JSTOR 3606420 .
Саксена, JP (1968). «Стохастическая оптимальная маршрутизация». Бизнес-исследования . 12 (1): 173–177. дои : 10.1007/BF01918326 . S2CID 10064660 .
Этвуд, Майкл Э.; Полсон, Питер Г. (1976). «Модель процесса решения проблем с кувшинами для воды». Когнитивная психология . 8 (2): 191–216. дои : 10.1016/0010-0285(76)90023-2 . S2CID 54388726 .
Рем, Мартин; Чу, Янг Иль (1982). «Программа с фиксированным пространством линейной сложности вывода для задачи трех сосудов» . Наука компьютерного программирования . 2 (2): 133–141. дои : 10.1016/0167-6423(82)90011-9 .
Томас, Гланфруд П. (1995). «Проблема кувшинов с водой: решения с точки зрения искусственного интеллекта и математики». Математика в школе . Том. 24, нет. 2. С. 34–37. JSTOR 30215221 .
Мюррей-Лассо, Массачусетс (2003). «Математические головоломки, мощные идеи, алгоритмы и компьютеры в обучении решению задач» . Журнал прикладных исследований и технологий . Том. 1, нет. 3. С. 215–234.
Лалчев, Здравко Воутов; Варбанова, Маргарита Генова; Вутова, Ирирна Здравкова (2009). «Геометрический метод Перлмана решения задач обливания жидкостью» .
Гетшалькс, Марк (2011). «Однопоточная маршрутизация через сеть». Проектирование цепочек поставок . Международная серия по исследованию операций и науке управления. Том. 161. стр. 155–180. дои : 10.1007/978-1-4419-6512-7_6 . ISBN 978-1-4419-6511-0 .

Ссылки

^ Вайсштейн, Эрик В. «Задача о трех кувшинах» . mathworld.wolfram.com . Проверено 21 января 2020 г.
^ «Решение задач декантации с помощью теории графов» . Вольфрам Альфа .
^ «Задачи декантации и алгоритм Дейкстры» . Франсиско Бланко-Сильва . 29 июля 2016 г. Проверено 25 мая 2020 г.
^ Подсказка к загадке № 22: Загадка с твердой водой на 3 и 5 литров . Puzzles.nigelcoldwell.co.uk. Проверено 9 июля 2017 г.
^ Как не умереть с математикой , получено 25 мая 2020 г.
^ «Выберите свой объем» . блестящий.орг . Проверено 22 сентября 2020 г.
^ Вайсштейн, Эрик В. «Задача о трех кувшинах» . mathworld.wolfram.com . Проверено 27 августа 2019 г.

[1] Вайсштейн, Эрик В. «Задача о трех кувшинах» . mathworld.wolfram.com . Проверено 21 января 2020 г.

[2] «Решение задач декантации с помощью теории графов» . Вольфрам Альфа .

[3] «Задачи декантации и алгоритм Дейкстры» . Франсиско Бланко-Сильва . 29 июля 2016 г. Проверено 25 мая 2020 г.

[4] Подсказка к загадке № 22: Загадка с твердой водой на 3 и 5 литров . Puzzles.nigelcoldwell.co.uk. Проверено 9 июля 2017 г.

[5] Как не умереть с математикой , получено 25 мая 2020 г.

[6] «Выберите свой объем» . блестящий.орг . Проверено 22 сентября 2020 г.

[Weisstein2019-7] Вайсштейн, Эрик В. «Задача о трех кувшинах» . mathworld.wolfram.com . Проверено 27 августа 2019 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]