Колонка Тейлора

Движение жидкости над и под движущимся объектом вынуждено циркулировать и, таким образом, ограничивается пределами столбца, вытянутого объектом по оси вращения.

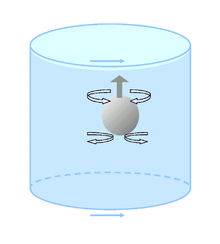
Столбец Тейлора — явление гидродинамики, возникающее в результате эффекта Кориолиса . Он был назван в честь Джеффри Ингрэма Тейлора . Вращающиеся жидкости, возмущенные твердым телом, имеют тенденцию образовывать столбцы, параллельные оси вращения, называемые столбцами Тейлора.

Объект, движущийся параллельно оси вращения во вращающейся жидкости, испытывает большую силу сопротивления, чем в невращающейся жидкости. Например, сильно плавучий мяч (например, мяч для пинг-понга) будет подниматься на поверхность медленнее, чем в невращающейся жидкости. Это связано с тем, что жидкость на пути отталкиваемого мяча имеет тенденцию циркулировать обратно в точку, от которой он был смещен, из-за эффекта Кориолиса. Чем выше скорость вращения, тем меньше радиус инерционной окружности, по которой движется жидкость.

Единица жидкости (представленная черной точкой) отталкивается обратно в точку, из которой она была смещена.

В невращающейся жидкости жидкость отделяется над поднимающимся шаром и закрывается под ним, оказывая шару относительно небольшое сопротивление. Во вращающейся жидкости шару необходимо вытолкнуть вверх целый столб жидкости над собой и тащить за собой целый столб жидкости, чтобы подняться на поверхность.

Таким образом, вращающаяся жидкость обладает некоторой степенью жесткости.

История

Колонны Тейлора впервые наблюдал Уильям Томсон, лорд Кельвин , в 1868 году. Колонны Тейлора были представлены на демонстрациях лекций Кельвина в 1881 году. и Джон Перри в 1890 году. Это явление объясняется теоремой Тейлора-Прудмана и исследовалось Тейлором. Милость, Стюартсон, и Максворти — среди прочих.

Теория

Столбец Тейлора в жидкости

Колонки Тейлора были тщательно изучены. Для Re <<1, Ek <<1, Ro <<1, уравнения сопротивления для цилиндра радиуса a было найдено следующее соотношение.

$F={\frac {16}{3}}\rho a^{3}\Omega U$

Чтобы получить это, Мур и Саффман решили линеаризованное уравнение Навье – Стокса в цилиндрических координатах: где некоторые из вертикальных и радиальных составляющих вязкого члена считаются малыми по сравнению с членом Кориолиса:

$-2\Omega v=-{\frac {1}{\rho }}{\frac {\partial p}{\partial r}}$

$2\Omega u=\nu \left({\frac {\partial ^{2}v}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial v}{\partial r}}-{\frac {v^{2}}{r}}\right)$

$0=-{\frac {1}{\rho }}{\frac {\partial p}{\partial z}}+\nu \left({\frac {\partial ^{2}w}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial w}{\partial r}}\right)$

Для решения этих уравнений мы также включаем условие сохранения объема:

${\frac {1}{r}}{\frac {\partial (ur)}{\partial r}}+{\frac {\partial w}{\partial z}}=0$

Мы используем соотношение совместимости Экмана для этой геометрии, чтобы ограничить форму скорости на поверхности диска:

$w-U=\pm {\frac {1}{2}}{\sqrt {\frac {\nu }{\Omega }}}{\frac {1}{r}}{\frac {\partial (rv)}{\partial r}}$

Полученные поля скорости можно решить в терминах функций Бесселя .

$u=-{\frac {\nu }{2\Omega }}\int \limits _{0}^{\infty }k^{2}A(k)J_{1}(kr)e^{-\nu k^{3}z/2\Omega }dk$

$v=\int \limits _{0}^{\infty }A(k)J_{1}(kr)e^{-\nu k^{3}z/2\Omega }dk$

$w=-\int \limits _{0}^{\infty }A(k)J_{0}(kr)e^{-\nu k^{3}z/2\Omega }dk$

при этом для Ek <<1 функция A(k) определяется выражением:

$A(k)={\frac {2Ua}{\pi }}\left(\cos ka-{\frac {\sin ka}{ka}}\right)$

Интегрируя уравнение для v , мы можем найти давление и, следовательно, силу сопротивления, заданную первым уравнением.

Дальнейшее чтение

• Бреннер, Майкл П.; Стоун, Ховард А. (май 2000 г.). «Современная классическая физика через работы Г.И. Тейлора» . Физика сегодня . 53 (5): 30–35. Бибкод : 2000PhT....53e..30B . дои : 10.1063/1.883100 .

Внешние ссылки

• Колонки Тейлора (Марта Бакли, Массачусетский технологический институт)
• Динамика жидкости проигрывателя пластинок: эксперимент с колонкой Тейлора (Spin Lab Калифорнийского университета в Лос-Анджелесе)