Подкасательная

Субкасательная и родственные понятия для кривой ( черной в данной точке P. ) Касательная и нормальная линии показаны зеленым и синим цветом соответственно. Показаны расстояния по ординате ( AP ), касательной ( TP ), субкасательной ( TA ), нормальной ( PN ) и субнормальной ( AN ). Угол φ — это угол наклона касательной или касательный угол.

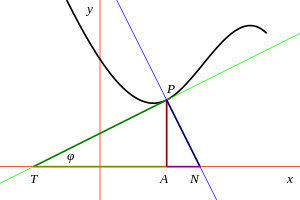
В геометрии субкасательная и связанные с ней термины представляют собой определенные отрезки прямой, определяемые с помощью касательной к кривой в данной точке и координатных осей . Сегодня эти термины несколько архаичны, но широко использовались до начала 20 века.

Определения

Пусть P = ( x , y ) будет точкой на данной кривой с A = ( x , 0) ее проекцией на ось x . Нарисуйте касательную к кривой в точке P и пусть T будет точкой, где эта линия пересекает ось x . Тогда TA определяется как субкасательная в точке P . Аналогично, если нормаль к кривой в точке P пересекает ось x в точке N, то AN называется субнормальной . В этом контексте длины PT и PN называются касательной и нормальной линией , не путать с касательной и нормальной линией, которые также называются касательной и нормальной линией.

Уравнения

Пусть φ — угол наклона касательной относительно оси x ; это также известно как тангенциальный угол . Затем

$\tan \varphi ={\frac {dy}{dx}}={\frac {AP}{TA}}={\frac {AN}{AP}}.$

Итак, подкасательная

$y\cot \varphi ={\frac {y}{\tfrac {dy}{dx}}},$

и субнормальное это

$y\tan \varphi =y{\frac {dy}{dx}}.$

Норма определяется

$y\sec \varphi =y{\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}},$

а тангенс определяется выражением

$y\csc \varphi ={\frac {y}{\tfrac {dy}{dx}}}{\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}.$

определения

понятия для кривой ( черной ) в данной точке P. Полярный субкасательный и связанные с ним Касательная и нормальная линии показаны зеленым и синим цветом соответственно. Показанные расстояния — это радиус ( OP ), полярная субкасательная ( OT ) и полярная субнормаль ( ON ). Угол θ представляет собой радиальный угол и угол ψ наклона касательной к радиусу или полярный тангенциальный угол.

Пусть P = ( r , θ) будет точкой на данной кривой, определяемой полярными координатами , и пусть O обозначает начало координат. линию Проведите через O , перпендикулярную OP и пусть теперь T будет точкой, где эта линия пересекает касательную к кривой в точке P. , Аналогично, пусть теперь N будет точкой, где нормаль к кривой пересекает линию. Тогда OT и ON называются соответственно полярной субкасательной и полярной субнормалью кривой в точке P .

Полярные

Пусть ψ — угол между касательной и лучом OP ; это также известно как полярный тангенциальный угол. Затем

$\tan \psi ={\frac {r}{\tfrac {dr}{d\theta }}}={\frac {OP}{ON}}={\frac {OT}{OP}}.$

Итак, полярный субтангенс

$r\tan \psi ={\frac {r^{2}}{\tfrac {dr}{d\theta }}},$

и субнормальное это

$r\cot \psi ={\frac {dr}{d\theta }}.$

Ссылки

• Дж. Эдвардс (1892). Дифференциальное исчисление . Лондон: MacMillan and Co., стр. 150 , 154.

• Б. Уильямсон «Субкасательная и субнормальная» и «Полярная субкасательная и полярная субнормальная» в «Элементарном трактате по дифференциальному исчислению» (1899), стр. 215, 223 Интернет-архив.