Уоткинс язвит
| Уоткинс язвит | |
|---|---|
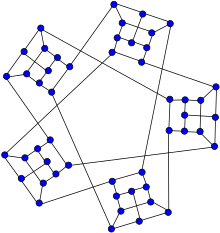 Уоткинс язвит | |
| Назван в честь | Джей Джей Уоткинс |
| Вершины | 50 |
| Края | 75 |
| Радиус | 7 |
| Диаметр | 7 |
| Обхват | 5 |
| Автоморфизмы | 5 |
| Хроматическое число | 3 |
| Хроматический индекс | 4 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Снарк |
| Таблица графиков и параметров | |
В математической области теории графов снарк Уоткинса представляет собой снарк с 50 вершинами и 75 ребрами . [1] [2] Он был открыт Джоном Дж. Уоткинсом в 1989 году. [3]
В качестве снарка граф Уоткинса представляет собой связный без мостов кубический граф с хроматическим индексом , равным 4. Снарк Уоткинса также непланарен и негамильтонов . Имеет толщину книги 3 и номер очереди 2. [4]
Другой известный снарк на 50 вершинах — это снарк Секереса , пятый известный снарк, открытый Джорджем Секересом в 1973 году. [5]
Галерея
[ редактировать ]
Края
[ редактировать ][[1,2], [1,4], [1,15], [2,3], [2,8], [3,6], [3,37], [4,6], [4,7], [5,10], [5,11], [5,22], [6,9], [7,8], [7,12], [8,9], [9,14], [10,13], [10,17], [11,16], [11,18], [12,14], [12,33], [13,15], [13,16], [14,20], [15,21], [16,19], [17,18], [17,19], [18,30], [19,21], [20,24], [20,26], [21,50], [22,23], [22,27], [23,24], [23,25], [24,29], [25,26], [25,28], [26,31], [27,28], [27,48], [28,29], [29,31], [30,32], [30,36], [31,36], [32,34], [32,35], [33,34], [33,40], [34,41], [35,38], [35,40], [36,38], [37,39], [37,42], [38,41], [39,44], [39,46], [40,46], [41,46], [42,43], [42,45], [43,44], [43,49], [44,47], [45,47], [45,48], [47,50], [48,49], [49,50]]
Ссылки
[ редактировать ]- ^ Вайсштейн, Эрик В. «Уоткинс Снарк» . Математический мир .
- ^ Уоткинс, Дж. Дж. и Уилсон, Р. Дж. «Обзор снарков». В книге «Теория графов, комбинаторика и приложения» (под ред. Ю. Алави, Г. Чартрана, О. Р. Оллермана и А. Дж. Швенка ). Нью-Йорк: Уайли, стр. 1129–1144, 1991.
- ^ Уоткинс, Джей Джей «Снаркс». Энн. Нью-Йоркская академия. наук. 576, 606–622, 1989.
- ^ Вольц, Джессика; Проектирование линейных макетов с помощью SAT . Магистерская диссертация, Тюбингенский университет, 2018 г.
- ^ Секерес, Г. (1973). «Многогранные разложения кубических графов» . Бык. Австрал. Математика. Соц . 8 (3): 367–387. дои : 10.1017/S0004972700042660 .
 | Эта комбинаторике статья, посвященная , незавершена . Вы можете помочь Википедии, расширив ее . |