Поток точки застоя

В гидродинамике поток в точке торможения относится к потоку жидкости в окрестности точки торможения (в двумерных потоках) или линии торможения (в трехмерных потоках), при котором точка/линия торможения относится к точке/ линия, где скорость равна нулю в невязком приближении. В потоке конкретно рассматривается класс точек застоя, известных как седловые точки, в которых входящие линии тока отклоняются и направляются наружу в другом направлении; прогибы линий тока направляются сепаратрисами. Течение в окрестности критической точки или линии, как правило, можно описать с помощью теории потенциального потока , хотя эффектами вязкости нельзя пренебрегать, если критическая точка лежит на твердой поверхности.

Поток в критической точке без твердых поверхностей

Когда два потока двумерной или осесимметричной природы сталкиваются друг с другом, создается плоскость застоя, где входящие потоки отклоняются по касательной наружу; таким образом, на плоскости торможения компонента скорости, нормальная к этой плоскости, равна нулю, тогда как тангенциальная составляющая отлична от нуля. В окрестности критической точки можно описать локальное описание поля скорости.

Общее трехмерное поле скоростей

Поток критической точки соответствует линейной зависимости от координат, которую можно описать в декартовых координатах $(x,y,z)$ с компонентами скорости $(v_{x},v_{y},v_{z})$ следующее

$v_{x}=\alpha x,\quad v_{y}=\beta y,\quad v_{z}=\gamma z$

где $(\alpha ,\beta ,\gamma )$ – константы (или зависящие от времени функции), называемые скоростями деформации; три скорости деформации не являются полностью произвольными, поскольку уравнение непрерывности требует $\alpha +\beta +\gamma =0$, то есть только две из трех констант являются независимыми. Мы будем считать $\gamma <0\leq \alpha$ так что поток направлен к точке застоя в $z$ направлении и от точки застоя в $x$ направление. Не ограничивая общности, можно предположить, что $\beta \geq \alpha$. Поле потока можно разделить на различные типы на основе одного параметра.

$\lambda ={\frac {\alpha -\beta }{\alpha +\beta }}$

Плоское течение в критической точке

Двумерное течение критической точки относится к случаю $\beta =0\,(\lambda =1)$. Поле течения описывается следующим образом

$v_{x}=kx,\quad v_{z}=-kz$

где мы позволяем $k=\alpha =-\gamma >0$. Это поле течения исследовал еще в 1934 году Г.И. Тейлор . В лаборатории это поле течения создается с помощью четырехмельничного аппарата, хотя в турбулентных потоках эти поля течения встречаются повсеместно.

Осесимметричное течение в критической точке

Осесимметричное течение в критической точке соответствует $\alpha =\beta \,(\lambda =0)$. Поле течения можно просто описать в цилиндрической системе координат. $(r,\theta ,z)$ с компонентами скорости $(v_{r},0,v_{z})$ следующее

$v_{r}=kr,\quad v_{z}=-2kz$

где мы позволяем $k=\alpha =\beta =-\gamma /2>0$.

Радиальные застойные потоки

В радиальных застойных течениях вместо застойной точки мы имеем застойный круг, а застойная плоскость заменяется застойным цилиндром. Радиальное застойное течение описывается в цилиндрической системе координат $(r,z)$ с компонентами скорости $(v_{r},v_{z})$ следующее

$v_{r}=-k\left(r-{\frac {r_{s}^{2}}{r}}\right),\quad v_{z}=2kz$

где $r_{s}$ - расположение застойного цилиндра.

Поток Хименца

Двумерное течение в критической точке

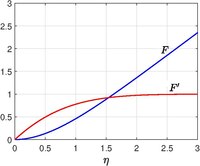
Течение из-за наличия твердой поверхности при $z=0$ плоское течение в критической точке было впервые описано Карлом Хименцем в 1911 году. чьи численные расчеты решений были позже улучшены Лесли Ховартом . Известным примером применимости течения Хименца является прямая линия торможения, возникающая при обтекании круглого цилиндра.

Твердая поверхность лежит на $xy$. Согласно теории потенциального потока, движение жидкости описывается функцией тока $\psi$ и компоненты скорости $(v_{x},0,v_{z})$ даны

$\psi =kxz,\quad v_{x}=kx,\quad v_{z}=-kz.$

Линия застоя для этого течения равна $(x,y,z)=(0,y,0)$. Компонент скорости $v_{x}$ не равно нулю на твердой поверхности, что указывает на то, что указанное выше поле скорости не удовлетворяет граничным условиям прилипания на стенке. Чтобы найти компоненты скорости, удовлетворяющие граничному условию прилипания, принимают следующий вид

$\psi ={\sqrt {\nu k}}xF(\eta ),\quad \eta ={\frac {z}{\sqrt {\nu /k}}}$

где $\nu$ – кинематическая вязкость и ${\sqrt {\nu /k}}$ — характерная толщина, при которой вязкие эффекты значительны. Существование постоянной величины толщины вязких эффектов обусловлено конкурирующим балансом между конвекцией жидкости, направленной к поверхности твердого тела, и вязкой диффузией, направленной от поверхности. Таким образом, завихренность, возникающая на поверхности твердого тела, способна диффундировать лишь на расстояния порядка ${\sqrt {\nu /k}}$; Аналогичные ситуации, напоминающие это поведение, возникают в асимптотическом профиле всасывания и закрученном потоке фон Кармана . компоненты скорости, давление и уравнения Навье – Стокса Тогда примут вид

$v_{x}=kxF',\quad v_{z}=-{\sqrt {\nu k}}F,\quad {\frac {p_{o}-p}{\rho }}={\frac {1}{2}}k^{2}x^{2}+k\nu F'+{\frac {1}{2}}k\nu F^{2}$

$F'''+FF''-F'^{2}+1=0$

Требования, которые $(v_{x},v_{z})=(0,0)$ в $z=0$ и это $v_{x}\rightarrow kx$ как $z\rightarrow \infty$ перевести на

$F(0)=0,\ F'(0)=0,F'(\infty )=1.$

Условие для $v_{z}$ как $z\rightarrow \infty$ не может быть задана и получается как часть решения. Сформулированная здесь задача представляет собой частный случай пограничного слоя Фолкнера-Скана . Решение может быть получено путем численного интегрирования и показано на рисунке. Асимптотическое поведение для больших $\eta \rightarrow \infty$ являются

$F\sim \eta -0.6479,\quad v_{x}\sim kx,\quad v_{z}\sim -k(z-\delta ^{*}),\quad \delta ^{*}=0.6479\delta$

где $\delta ^{*}$ - толщина смещения .

Поток в критической точке с подвижной стенкой

Течение Хименца, когда твердая стенка перемещается с постоянной скоростью. $U$ вдоль $x$ была решена Роттом (1956). Эта задача описывает течение в окрестности передней линии торможения, возникающее при обтекании вращающегося цилиндра. Требуемая функция потока:

$\psi ={\sqrt {\nu k}}xF(\eta )+U\delta \int _{0}^{\eta }G(\eta )d\eta$

где функция $G(\eta )$ удовлетворяет

$G''+FG'-F'G=0,\quad G(0)=1,\quad G(\infty )=0$

Решение приведенного выше уравнения имеет вид $G(\eta )=F''(\eta )/F''(0).$

Косое течение в критической точке

Если набегающий поток перпендикулярен линии застоя, но приближается под углом, то внешний поток не является потенциальным, а имеет постоянную завихренность. $-\zeta _{o}$. Соответствующая функция тока для потока в наклонной критической точке определяется выражением

$\psi =kxz+{\frac {1}{2}}\zeta _{o}z^{2}$

Вязкие эффекты, обусловленные наличием твердой стенки, изучал Стюарт (1959): Тамада (1979) и Доррепаал (1986). В их подходе функция потока принимает вид

$\psi ={\sqrt {\nu k}}xF(\eta )+\zeta _{o}\delta ^{2}\int _{0}^{\eta }H(\eta )d\eta$

где функция $H(\eta )$

$H''+FH'-F'H=0,\quad H(0)=0,\quad H'(\infty )=1$.

Поток Хомана

Поток Хомана с впрыском

Поток Хомана с отсосом

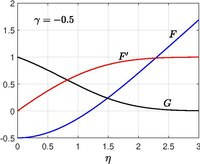
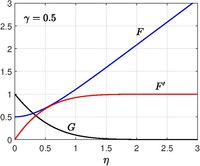
Решение для осесимметричного течения в критической точке при наличии твердой стенки было впервые получено Хоманном (1936). Типичным примером такого течения является прямая критическая точка, возникающая при обтекании сферы. Пол А. Либби (1974) (1976) расширил работу Хоманна, позволив твердой стенке перемещаться вдоль своей плоскости с постоянной скоростью и обеспечивая постоянное всасывание или впрыскивание на твердую поверхность.

Решение этой задачи получено в цилиндрической системе координат $(r,\theta ,z)$ представив

$\eta ={\frac {z}{\sqrt {\nu /k}}},\quad \gamma =-{\frac {V}{2{\sqrt {k\nu }}}},\quad v_{r}=krF'(\eta )+U\cos \theta G(\eta ),\quad v_{\theta }=-U\sin \theta G(\eta ),\quad v_{z}=-2{\sqrt {k\nu }}F(\eta )$

где $U$ - поступательная скорость стенки и $V$ — скорость впрыска (или всасывания) у стенки. Задача является осесимметричной только тогда, когда $U=0$. Давление определяется

${\frac {p-p_{o}}{\rho }}=-{\frac {1}{2}}k^{2}r^{2}-2k\nu (F^{2}+F')$

Тогда уравнения Навье – Стокса сводятся к

${\begin{aligned}F'''+2FF''-F'^{2}+1&=0,\\G''+2FG'-F'G&=0\end{aligned}}$

наряду с граничными условиями,

$F(0)=\gamma ,\quad F'(0)=0,\quad F'(\infty )=1,\quad G(0)=1,\quad G(\infty )=0.$

Когда $U=V=0$, классическая задача Хомана восстановлена.

Плоские противотоки

Согласно потенциальной теории, струи, выходящие из щелевых струй, создают точку застоя между ними. Течение вблизи критической точки можно изучить с помощью автомодельного решения. Эта установка широко используется в экспериментах по горению . Первоначальное исследование набегающих застойных потоков принадлежит К. Вангу. Пусть две жидкости с постоянными свойствами обозначаются суффиксом $1({\text{top}}),\ 2({\text{bottom}})$ Текущие в противоположном направлении сталкиваются, и предположим, что две жидкости несмешивающиеся, а граница раздела (расположенная в точке $y=0$) плоская. Скорость определяется выражением

$u_{1}=k_{1}x,\quad v_{1}=-k_{1}y,\quad u_{2}=k_{2}x,\quad v_{2}=-k_{2}y$

где $k_{1},\ k_{2}$ – скорости деформации жидкостей. На границе раздела скорости, касательное напряжение и давление должны быть непрерывными.Вводя самоподобное преобразование,

$\eta _{1}={\sqrt {\frac {\nu _{1}}{k_{1}}}}y,\quad u_{1}=k_{1}xF_{1}',\quad v_{1}=-{\sqrt {\nu _{1}k_{1}}}F_{1}$

$\eta _{2}={\sqrt {\frac {\nu _{2}}{k_{2}}}}y,\quad u_{2}=k_{2}xF_{2}',\quad v_{2}=-{\sqrt {\nu _{2}k_{2}}}F_{2}$

уравнения результатов,

$F_{1}'''+F_{1}F_{1}''-F_{1}'^{2}+1=0,\quad {\frac {p_{o1}-p_{1}}{\rho _{1}}}={\frac {1}{2}}k_{1}^{2}x^{2}+k_{1}\nu _{1}F_{1}'+{\frac {1}{2}}k_{1}\nu _{1}F_{1}^{2}$

$F_{2}'''+F_{2}F_{2}''-F_{2}'^{2}+1=0,\quad {\frac {p_{o2}-p_{2}}{\rho _{2}}}={\frac {1}{2}}k_{2}^{2}x^{2}+k_{2}\nu _{2}F_{2}'+{\frac {1}{2}}k_{2}\nu _{2}F_{2}^{2}.$

Условия непроникновения на границе раздела и условия набегающего потока вдали от плоскости застоя становятся

$F_{1}(0)=0,\quad F_{1}'(\infty )=1,\quad F_{2}(0)=0,\quad F_{2}'(-\infty )=1.$

Но уравнения требуют еще двух граничных условий. В $\eta =0$, тангенциальные скорости $u_{1}=u_{2}$, касательное напряжение $\rho _{1}\nu _{1}\partial u_{1}/\partial y=\rho _{2}\nu _{2}\partial u_{2}/\partial y$ и давление $p_{1}=p_{2}$ являются непрерывными. Поэтому,

${\begin{aligned}k_{1}F_{1}'(0)&=k_{2}F_{2}'(0),\\\rho _{1}{\sqrt {\nu _{1}k_{1}^{3}}}F_{1}''(0)&=\rho _{2}{\sqrt {\nu _{2}k_{2}^{3}}}F_{2}''(0),\\p_{o1}-\rho _{1}\nu _{1}k_{1}F_{1}'(0)&=p_{o2}-\rho _{2}\nu _{2}k_{2}F_{2}'(0).\end{aligned}}$

где $\rho _{1}k_{1}^{2}=\rho _{2}k_{2}^{2}$ (из внешней невязкой задачи). Оба $F_{i}'(0),F_{i}''(0)$ не известны априорно , но выводятся из условий совмещения. Третье уравнение определяет изменение внешнего давления. $p_{o1}-p_{o2}$ из-за эффекта вязкости. Таким образом, есть только два параметра, которые управляют потоком:

$\Lambda ={\frac {k_{1}}{k_{2}}}=\left({\frac {\rho _{2}}{\rho _{1}}}\right)^{1/2},\quad \Gamma ={\frac {\nu _{2}}{\nu _{1}}}$

тогда граничные условия станут

$F_{1}'(0)=\Lambda F_{2}'(0),\quad F_{1}''(0)={\sqrt {\frac {\Gamma }{\Lambda }}}F_{2}''(0)$.