Кубосвязные циклы
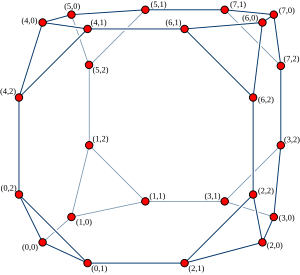
В теории графов кубосвязные циклы — это неориентированный кубический граф образованный заменой каждой вершины графа гиперкуба циклом , . Он был представлен Preparata & Vuillemin (1981) для использования в качестве топологии сети в параллельных вычислениях .
Определение
[ редактировать ]Кубосвязные циклы порядка n (обозначаемые CCC n ) можно определить как граф, сформированный из набора n 2 н узлы, индексированные парами чисел ( x , y ), где 0 ≤ x < 2 н и 0 ≤ y < n . Каждый такой узел соединен с тремя соседями: ( x , ( y + 1) mod n ) , ( x , ( y − 1) mod n ) и ( x ⊕ 2 и , y ) , где «⊕» обозначает побитовую исключающую операцию или операцию над двоичными числами.
Этот граф также можно интерпретировать как результат замены каждой вершины n -мерного графа гиперкуба на n -вершинный цикл. Вершины графа гиперкуба индексируются числами x , а позиции внутри каждого цикла — числами y .
Характеристики
[ редактировать ]Кубосвязные циклы порядка n — это Кэли граф группа , которая действует на двоичные слова длины n путем вращения и переворачивания битов слова. [1] Генераторы, используемые для формирования этого графа Кэли из группы, представляют собой элементы группы, которые действуют, поворачивая слово на одну позицию влево, поворачивая его на одну позицию вправо или переворачивая его первый бит. Поскольку это граф Кэли, он вершинно-транзитивен : существует симметрия графа, отображающая любую вершину в любую другую вершину.
Диаметр для кубосвязных циклов порядка n равен 2 n + ⌊n/2⌋ − 2 любого n ≥ 4; самая дальняя точка от ( x , y ) - (2 н − x − 1, ( y + n /2) mod n ). [2] Сикора и Вртё (1993) показали, что число пересечений CCC n равно ((1/20) + o(1)) 4 н .
Согласно гипотезе Ловаса , граф кубически-связных циклов всегда должен содержать гамильтонов цикл , и теперь известно, что это верно. В более общем смысле, хотя эти графы не являются панциклическими , они содержат циклы всех возможных четных длин, кроме ограниченного числа, а когда n нечетно, они также содержат множество возможных нечетных длин циклов. [3]
Приложение для параллельной обработки
[ редактировать ]Циклы, связанные с кубом, были исследованы Preparata & Vuillemin (1981) , которые применили эти графики в качестве схемы взаимосвязей сети, соединяющей процессоры в параллельном компьютере . В этом приложении циклы, связанные с кубом, обладают преимуществами связности гиперкубов, но при этом требуют всего три соединения на процессор. Препарата и Вийемен показали, что планарная планировка, основанная на этой сети, имеет оптимальную площадь × время. 2 сложность многих задач параллельной обработки.
Примечания
[ редактировать ]Ссылки
[ редактировать ]- Акерс, Шелдон Б.; Кришнамурти, Балакришнан (1989), «Теоретико-групповая модель для симметричных межсетевых сетей», IEEE Transactions on Computers , 38 (4): 555–566, doi : 10.1109/12.21148 .
- Аннекстайн, Фред; Баумслаг, Марк; Розенберг, Арнольд Л. (1990), «Графы групповых действий и параллельные архитектуры», SIAM Journal on Computing , 19 (3): 544–569, doi : 10.1137/0219037 .
- Фриш, Иван; Гавел, Иван; Либл, Петр (1997), «Диаметр циклов, связанных с кубом», Information Processing Letters , 61 (3): 157–160, doi : 10.1016/S0020-0190(97)00013-6 .
- Джерма, Энн; Хадеманн, Мари-Клод; Сотто, Доминик (1998), «Циклы в графе кубически-связных циклов», Discrete Applied Mathematics , 83 (1–3): 135–155, doi : 10.1016/S0166-218X(98)80001-2 , MR 1622968 .
- Препарата, Франко П .; Вуйемен, Жан (1981), «Циклы, связанные с кубом: универсальная сеть для параллельных вычислений», Communications of the ACM , 24 (5): 300–309, doi : 10.1145/358645.358660 , hdl : 2142/74219 , S2CID 8538576 .
- Сикора, Ондрей; Вртё, Имрих (1993), «О числах пересечений гиперкубов и связанных циклов куба», BIT Numerical Mathematics , 33 (2): 232–237, doi : 10.1007/BF01989746 , hdl : 11858/00-001M-0000-002D- 92E4-9 , S2CID 15913153 .