Сообщающиеся сосуды

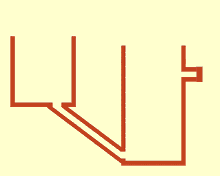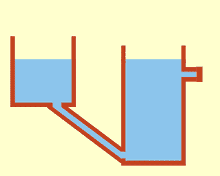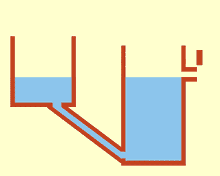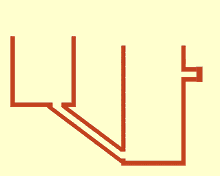
Сообщающиеся сосуды или сообщающиеся вазы [1] представляют собой набор емкостей, содержащих однородную жидкость и соединенных достаточно далеко ниже верха жидкости: когда жидкость оседает, ее уровень уравновешивается до одного и того же уровня во всех емкостях независимо от формы и объема емкостей. Если в один сосуд добавить дополнительную жидкость, то жидкость снова найдет новый равный уровень во всех соединенных сосудах. Это было обнаружено Саймоном Стевином как следствие закона Стевина . [2] Это происходит потому, что сила тяжести и давление в каждом сосуде постоянны ( гидростатическое давление ). [3]
Блез Паскаль доказал в семнадцатом веке, что давление, оказываемое на молекулу жидкости, передается полностью и с одинаковой интенсивностью во все стороны.
Приложения
[ редактировать ]Со времен Древнего Рима концепция сообщающихся сосудов использовалась для внутреннего водопровода через водоносные горизонты и свинцовые трубы. Вода достигнет одинакового уровня во всех частях системы, которая действует как сообщающиеся сосуды, независимо от того, какая самая низкая точка у труб – хотя на практике самая низкая точка системы зависит от способности водопровода выдерживать воздействие воды. давление жидкости.

В городах часто используются водонапорные башни , чтобы городская водопроводная система выполняла функцию сообщающихся сосудов, распределяя воду на верхние этажи зданий под достаточным давлением.
Гидравлические прессы , использующие системы сообщающихся сосудов, широко используются в различных приложениях промышленных процессов.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Марио Бунге , Философия науки: от объяснения к обоснованию , 1998, ISBN 1412830834 , с. 369
- ^ Спеллман, Фрэнк Р.; Уайтинг, Нэнси Э. (2005). Справочник инженера-эколога по математике . ЦРК Пресс. ISBN 978-1-56670-681-0 .
- ^ Фонтана, Фабрицио; ДиКапуа Роберто (август 2005 г.). «Роль гидростатических парадоксов в формировании научной мысли студентов на академическом уровне». Европейский журнал физики . 26 (6): 1017–1030. Бибкод : 2005EJPh...26.1017F . дои : 10.1088/0143-0807/26/6/009 . S2CID 120595888 .