Кусочно-линейное продолжение

Симплициальное продолжение или кусочно-линейное продолжение (Алговер и Георг), с одним параметром — это метод продолжения , который хорошо подходит для небольших и средних пространств встраивания. Алгоуэр и Гнутцман обобщили алгоритм для вычисления многообразий более высокой размерности. и (Аллгоуэр и Шмидт).

Алгоритм рисования контуров представляет собой алгоритм симплициального продолжения, и, поскольку его легко визуализировать, он служит хорошим введением в алгоритм.

Контурное построение

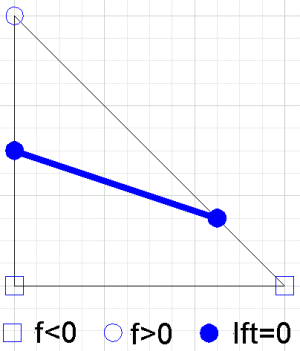
Задача построения контуров состоит в нахождении нулей (контуров) $f(x,y)=0\,$ ( $f(\cdot )\,$ гладкая скалярная функция) в квадрате $0\leq x\leq 1,0\leq y\leq 1\,$,

Квадрат делится на маленькие треугольники, обычно путем введения точек в углах обычной квадратной сетки. $ih_{x}\leq x\leq (i+1)h_{x}\,$, $jh_{y}\leq y\leq (j+1)h_{y}\,$, составив таблицу значений $f(x_{i},y_{j})\,$ на каждом углу $(i,j)\,$, а затем разделив каждый квадрат на два треугольника. Стоимость $f(x_{i},y_{j})\,$ в углах треугольника определяет уникальный кусочно-линейный интерполянт. $lf(x,y)\,$ к $f(\cdot )\,$ над каждым треугольником. Один из способов записи этого интерполянта на треугольнике с углами $(x_{0},y_{0}),~(x_{1},y_{1}),~(x_{2},y_{2})\,$ представляет собой систему уравнений

$(x,y)=(x_{0},y_{0})+(x_{1}-x_{0},y_{1}-y_{0})s+(x_{2}-x_{0},y_{2}-y_{0})t\,$

$0\leq s\,$

$0\leq t\,$

$s+t\leq 1\,$

$lf(x,y)=f(x_{0},y_{0})+(f(x_{1},y_{1})-f(x_{0},y_{0}))s+(f(x_{2},y_{2})-f(x_{0},y_{0}))t\,$

Первые четыре уравнения можно решить относительно $(s,t)\,$ (при этом исходный треугольник преобразуется в прямоугольный единичный треугольник), тогда оставшееся уравнение дает интерполированное значение $f(\cdot )\,$. По всей сетке треугольников этот кусочно-линейный интерполянт непрерывен.

Контур интерполянта на отдельном треугольнике представляет собой отрезок (это интервал на пересечении двух плоскостей). Уравнение прямой можно найти, однако точки, где линия пересекает края треугольника, являются конечными точками отрезка.

Контур кусочно-линейного интерполянта представляет собой набор кривых, составленных из этих отрезков. Любая точка на краю, соединяющем $(x_{0},y_{0})\,$ и $(x_{1},y_{1})\,$ можно записать как

$(x,y)=(x_{0},y_{0})+t(x_{1}-x_{0},y_{1}-y_{0}),\,$

с $t\,$ в $(0,1)\,$, а линейный интерполянт по краю равен

$f\sim f_{0}+t(f_{1}-f_{0})\,$

Итак, установка $f=0\,$

$t=-f_{0}/(f_{1}-f_{0})\,$ и $(x,y)=(x_{0},y_{0})-f_{0}*(x_{1}-x_{0},y_{1}-y_{0})/(f_{1}-f_{0})\,$

Поскольку это зависит только от значений на ребре, каждый треугольник, разделяющий это ребро, будет создавать одну и ту же точку, поэтому контур будет непрерывным. Каждый треугольник можно протестировать независимо, и если все отмечены галочкой, можно найти весь набор контурных кривых.

Кусочно-линейное продолжение

Кусочно-линейное продолжение аналогично контурному построению (Добкин, Леви, Терстон и Уилкс). но в более высоких измерениях. Алгоритм основан на следующих результатах:

Лемма 1

Если F(x) отображает $\mathbb {R} ^{n}$ в $\mathbb {R} ^{n-1}$, существует единственный линейный интерполянт на '(n-1)'-мерном симплексе , который согласуется со значениями функции в вершинах симплекса.

'(n-1)'-мерный симплекс имеет n вершин, и функция F присваивает каждой 'n'-вектор. Симплекс выпуклый , и любая точка внутри симплекса представляет собой выпуклую комбинацию вершин. То есть:

Если x находится внутри (n-1)-мерного симплекса с n вершинами $v_{i}$, то существуют положительные скаляры $0<\alpha _{i}$ такой, что

$\mathbf {x} =\sum _{i}\alpha _{i}\mathbf {v} _{i}$

$\sum _{i}\alpha _{i}=1.\,$

Если вершины симплекса линейно независимы, то неотрицательные скаляры $\alpha$ уникальны для каждой точки x и называются барицентрическими координатами x. Определяют значение уникального интерполянта по формуле:

$LF=\sum _{i}\alpha _{i}F(\mathbf {v} _{i})$

Лемма 2

(n-1)-мерный симплекс можно проверить, чтобы определить, содержит ли он начало координат.

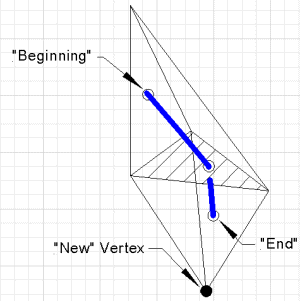
По сути, это два теста. Тот, который был использован первым, помечает вершины симплекса вектором знаков (+/-) координат вершины. Например, вершина (.5,-.2,1.) будет помечена (+,-,+). Симплекс называется полностью размеченным, если существует вершина, метка которой начинается со строки знаков «+» длины 0,1,2,3,4,...n. Полностью помеченный симплекс содержит окрестность начала координат. Это может показаться удивительным, но в основе этого результата лежит то, что для каждой координаты полностью помеченного симплекса существует вектор с «+» и другой с «-». Другими словами, наименьший куб с ребрами, параллельными осям координат и покрывающий симплекс, имеет пары граней на противоположных сторонах от 0 (т.е. «+» и «-» для каждой координаты).

Второй подход называется векторной маркировкой . Он основан на барицентрических координатах вершин симплекса. Первый шаг — найти барицентрические координаты начала координат, а затем проверка того, что симплекс содержит начало координат, заключается в том, что все барицентрические координаты положительны, а сумма меньше 1.

Лемма 3

Существует триангуляция (триангуляция Коксетера-Фрейденталя-Куна [1]), которая инвариантна относительно операции поворота. $P_{v_{i}}(v_{0},v_{1},...,v_{n}):=(v_{0},v_{1},...,v_{i-1},{\tilde {v}}_{i},v_{i+1},...,v_{n})$ где ${\tilde {v}}_{i}=\left\{{\begin{array}{lcl}v_{1}+v_{n}-v_{0}&&i=0\\v_{i+1}+v_{i-1}-v_{i}&\qquad \qquad &0\\v_{n-1}+v_{0}-v_{n}&&i=n\\\end{array}}\right.$