Скорость дрейфа

В физике электроны скорость дрейфа — это средняя скорость, достигаемая заряженными частицами, такими как , в материале под действием электрического поля . В общем, электрон в проводнике будет распространяться случайным образом со скоростью Ферми , в результате чего средняя скорость будет равна нулю. Приложение электрического поля добавляет к этому хаотическому движению небольшой результирующий поток в одном направлении; это дрейф.

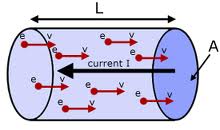
Скорость дрейфа пропорциональна току . В резистивном материале она также пропорциональна величине внешнего электрического поля. Таким образом, закон Ома можно объяснить с точки зрения скорости дрейфа. Самое элементарное выражение закона таково:

u=\mu E,

где $u$ — скорость дрейфа, $μ$ материала — подвижность электронов , а $E$ — электрическое поле . В системе МКС скорость дрейфа имеет единицы м/с, подвижность электронов - м ²/( В ·с) и электрическое поле, В/м.

Когда к проводнику приложена разность потенциалов, свободные электроны между последовательными столкновениями набирают скорость в направлении, противоположном электрическому полю (и теряют скорость при движении в направлении поля), таким образом, дополнительно приобретая компонент скорости в этом направлении. его случайной тепловой скорости. В результате возникает определенная малая дрейфовая скорость электронов, которая накладывается на хаотическое движение свободных электронов. Из-за этой скорости дрейфа возникает чистый поток электронов, противоположный направлению поля. Скорость дрейфа электронов обычно составляет порядка 10 ^-3 метров в секунду, тогда как тепловая скорость порядка 10 ⁶ метров в секунду.

Экспериментальная мера

Формула для оценки скорости дрейфа носителей заряда в материале постоянной площади поперечного сечения имеет вид: ^[1]

u={j \over nq},

где $u$ — скорость дрейфа электронов, $j$ — плотность тока, протекающего через материал, $n$ носителей заряда — плотность числа , а $q$ — заряд на носителе заряда.

Это также можно записать как:

j=nqu

Но плотность тока и скорость дрейфа j и u на самом деле являются векторами, поэтому это соотношение часто записывается как:

\mathbf {J} =\rho \mathbf {u} \,

где

\rho =nq

— плотность заряда (единица СИ: кулоны на кубический метр ).

С точки зрения основных свойств правоцилиндрического металлического током с омического проводника , в котором носителями заряда являются электроны , это выражение можно переписать как: ^{[ нужна ссылка ]}

u={m\;\sigma \Delta V \over \rho ef\ell },

где

$u$ снова скорость дрейфа электронов, м ⋅ с. ⁻¹
$m$ — молекулярная масса металла, кг.
$σ$ — электропроводность среды при рассматриваемой температуре, См / м .
$Δ V$ — напряжение, приложенное к проводнику, в В.
$ρ$ — плотность ( масса единицы объема ) проводника, кг ⋅ м. ⁻³
$e$ — элементарный заряд , в C
$f$ - количество свободных электронов на атом
$ℓ$ — длина проводника, м

Численный пример

Электричество чаще всего проводится по медным проводам. Медь имеет плотность 8,94 г/см. ³ и атомный вес 63,546 г/моль , то есть 140 685,5 моль/м ³. В одном моле любого элемента содержится 6,022 × 10 ²³ атомы ( число Авогадро ). Следовательно, через 1 м ³ меди насчитывается около 8,5 × 10 ²⁸ атомы ( 6,022 × 10 ²³ × 140 685,5 моль/м ³). Медь имеет один свободный электрон на атом, поэтому $n$ равно 8,5 × 10. ²⁸ электронов на кубический метр.

Предположим, ток $I$ = 1 ампер и провод диаметром 2 мм (радиус = 0,001 м ). Этот провод имеет площадь поперечного сечения $A$ π × ( 0,001 м ). ² = 3.14 × 10 ⁻⁶ м ² = 3,14 мм ². Заряд электрона q $\times$ = −1,6 одного 10 ⁻¹⁹ С. Таким образом, скорость дрейфа можно рассчитать: ${\begin{aligned}u&={I \over nAq}\\&={\frac {1{\text{C}}/{\text{s}}}{\left(8.5\times 10^{28}{\text{m}}^{-3}\right)\left(3.14\times 10^{-6}{\text{m}}^{2}\right)\left(1.6\times 10^{-19}{\text{C}}\right)}}\\&=2.3\times 10^{-5}{\text{m}}/{\text{s}}\end{aligned}}$

Размерный анализ : $u={\dfrac {\text{A}}{{\dfrac {\text{electron}}{{\text{m}}^{3}}}{\cdot }{\text{m}}^{2}\cdot {\dfrac {\text{C}}{\text{electron}}}}}={\dfrac {\dfrac {\text{C}}{\text{s}}}{{\dfrac {1}{\text{m}}}{\cdot }{\text{C}}}}={\dfrac {\text{m}}{\text{s}}}$

Следовательно, в этом проводе электроны движутся со скоростью 23 мкм/с . При переменном токе частотой 60 Гц это означает, что за полпериода (1/120 секунды) электроны в среднем смещаются на расстояние менее 0,2 мкм. В контексте, на один ампер около 3 × 10 ¹⁶ электроны будут проходить через точку контакта дважды за цикл. Но из примерно 1 × 10 ²² подвижных электронов на метр провода, это незначительная доля.

Для сравнения, скорость потока Ферми этих электронов (которую при комнатной температуре можно рассматривать как их приблизительную скорость в отсутствие электрического тока) составляет около 1570 км/с . ^[2]

См. также

Ссылки

^ Гриффитс, Дэвид (1999). Введение в электродинамику (3-е изд.). Река Аппер-Сэддл, Нью-Джерси: Прентис-Холл. п. 289 . ISBN 9780138053260 .
^ http://hyperphysicals.phy-astr.gsu.edu/hbase/electric/ohmmic.html Закон Ома, микроскопический вид, получено 16 ноября 2015 г.

Внешние ссылки

Закон Ома: микроскопический взгляд на гиперфизику

[1] Гриффитс, Дэвид (1999). Введение в электродинамику (3-е изд.). Река Аппер-Сэддл, Нью-Джерси: Прентис-Холл. п. 289 . ISBN 9780138053260 .

[2] ttp://hyperphysicals.phy-astr.gsu.edu/hbase/electric/ohmmic.html Закон Ома, микроскопический вид, получено 16 ноября 2015 г.

[1]

[2]