Код проверки четности низкой плотности

В теории информации код с низкой плотностью проверки четности ( LDPC ) — это линейный код с исправлением ошибок , метод передачи сообщения по зашумленному каналу передачи. Код LDPC строится с использованием разреженного графа Таннера (подкласса двудольного графа ). Коды LDPC являются кодами, приближающимися к пропускной способности , а это означает, что существуют практические конструкции, позволяющие устанавливать шумовой порог очень близко к теоретическому максимуму ( пределу Шеннона ) для симметричного канала без памяти. Шумовой порог определяет верхнюю границу шума канала, до которой вероятность потери информации может быть минимальной. Используя итеративные методы распространения доверия , коды LDPC можно декодировать во времени, линейном по длине блока.

Коды LDPC также известны как коды Галлагера , в честь Роберта Г. Галлагера , который разработал концепцию LDPC в своей докторской диссертации в Массачусетском технологическом институте в 1960 году. Однако коды LDPC требуют дорогостоящего итеративного декодирования, поэтому они не использовались в течение десятилетий. В 1993 году недавно изобретенные турбокоды продемонстрировали, что коды с итеративным декодированием могут значительно превосходить другие коды, использовавшиеся в то время, но турбокоды были запатентованы и требовали платы за использование. Это вызвало возобновление интереса к кодам LDPC, которые, как было показано, имели аналогичные характеристики, но были намного старше и не имели патентов. Теперь, когда срок действия фундаментального патента на турбокоды истек (29 августа 2013 г.), Коды LDPC до сих пор используются из-за своих технических достоинств.

Было показано, что коды LDPC обладают идеальными комбинаторными свойствами. В своей диссертации Галлагер показал, что LDPC-коды достигают границы Гилберта-Варшамова для линейных кодов с высокой вероятностью над двоичными полями. В 2020 году было показано, что LDPC-коды Галлагера достигают способности декодирования списков , а также достигают границы Гилберта-Варшамова для линейных кодов над общими полями.

История

Непрактично реализовать, когда он был впервые разработан Галлагером в 1963 году. Коды LDPC были забыты, пока его работа не была вновь открыта в 1996 году. Турбокоды , еще один класс кодов, приближающихся к пропускной способности, открытый в 1993 году, стал предпочтительной схемой кодирования в конце 1990-х годов и использовался для таких приложений, как сеть дальнего космоса и спутниковая связь . Затем коды LDPC вновь вызвали интерес как непатентованная альтернатива с аналогичными характеристиками. С тех пор достижения в области кодов с низкой плотностью проверки четности привели к тому, что они превзошли турбокоды с точки зрения минимального количества ошибок и производительности в более высоком диапазоне кодовых скоростей , в результате чего турбокоды лучше подходят только для более низких скоростей кодирования.

Приложения

В 2003 году код LDPC в стиле нерегулярного повторения (IRA) превзошел шесть турбокодов и стал кодом исправления ошибок в новом стандарте DVB-S2 для цифрового телевидения . Отборочный комитет DVB-S2 сделал оценку сложности декодера для предложений турбокода, используя гораздо менее эффективную архитектуру последовательного декодера, а не архитектуру параллельного декодера. Это вынудило предложения турбокодов использовать размеры кадров порядка половины размера кадра предложений LDPC.

В 2008 году LDPC превзошла сверточные турбокоды в качестве системы прямого исправления ошибок (FEC) для ITU-T G.hn. стандарта G.hn предпочел коды LDPC турбокодам из-за их меньшей сложности декодирования (особенно при работе со скоростями передачи данных, близкими к 1,0 Гбит/с), а также потому, что предложенные турбокоды демонстрировали значительный минимальный уровень ошибок в желаемом диапазоне работы.

Коды LDPC также используются для Ethernet 10GBASE-T , который передает данные со скоростью 10 гигабит в секунду по витой паре. С 2009 года коды LDPC также являются частью стандарта Wi-Fi 802.11 в качестве дополнительной части 802.11n и 802.11ac в спецификации PHY высокой пропускной способности (HT). LDPC является обязательной частью 802.11ax (Wi-Fi 6).

Некоторые системы OFDM добавляют дополнительную внешнюю коррекцию ошибок, которая исправляет случайные ошибки («минимальный уровень ошибок»), которые выходят за пределы внутреннего кода коррекции LDPC, даже при низкой частоте битовых ошибок .

Например:Код Рида-Соломона с кодовой модуляцией LDPC (RS-LCM) использует внешний код Рида-Соломона. Стандарты DVB-S2, DVB-T2 и DVB-C2 используют внешний код BCH для устранения остаточных ошибок после декодирования LDPC.

5G NR использует полярный код для каналов управления и LDPC для каналов данных.

Хотя код LDPC добился успеха в коммерческих жестких дисках, для полного использования его возможностей исправления ошибок в твердотельных накопителях требуется нетрадиционное детальное определение флэш-памяти, что приводит к увеличению задержки чтения из памяти. LDPC-в-SSD — это эффективный подход к развертыванию LDPC в SSD с очень небольшим увеличением задержки, который превращает LDPC в SSD в реальность. С тех пор LDPC широко применяется в коммерческих твердотельных накопителях как потребительского, так и корпоративного уровня крупными поставщиками систем хранения данных. Многие твердотельные накопители TLC (и более поздних версий) используют коды LDPC. Сначала предпринимается попытка быстрого жесткого декодирования (двоичного стирания), которая может вернуться к более медленному, но более мощному мягкому декодированию.

Оперативное использование

Коды LDPC функционально определяются разреженной матрицей проверки четности . Эта разреженная матрица часто генерируется случайным образом с учетом разреженности ограничений — конструкция кода LDPC обсуждается позже . Эти коды были впервые разработаны Робертом Галлагером в 1960 году.

Ниже приведен фрагмент графа примера кода LDPC с использованием нотации графа факторов Форни . В этом графе n узлов переменных в верхней части графа соединены с ( n − k ) узлами ограничений в нижней части графа.

Это популярный способ графического представления ( n , k ) LDPC-кода. Биты допустимого сообщения, помещенные в буквы Т в верхней части графика, удовлетворяют графическим ограничениям. В частности, все строки, соединяющиеся с узлом переменной (поле со знаком «=»), имеют одно и то же значение, а все значения, соединяющиеся с узлом фактора (поле со знаком «+»), должны суммироваться по модулю два до нуля (в другими словами, их сумма должна составлять четное число или должно быть четное количество нечетных значений).

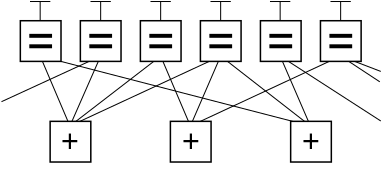
Если игнорировать любые строки, выходящие за пределы изображения, существует восемь возможных шестибитовых строк, соответствующих допустимым кодовым словам: (т. е. 000000, 011001, 110010, 101011, 111100, 100101, 001110, 010111). Этот фрагмент кода LDPC представляет собой трехбитное сообщение, закодированное как шесть бит. Здесь используется избыточность, чтобы увеличить вероятность восстановления после ошибок канала. Это (6, 3) линейный код с n = 6 и k = 3.

Опять игнорируя линии, выходящие за пределы изображения, матрица проверки четности, представляющая этот фрагмент графа, имеет вид

$\mathbf {H} ={\begin{pmatrix}1&1&1&1&0&0\\0&0&1&1&0&1\\1&0&0&1&1&0\\\end{pmatrix}}.$

В этой матрице каждая строка представляет одно из трех ограничений проверки четности, а каждый столбец представляет один из шести бит полученного кодового слова.

В этом примере восемь кодовых слов можно получить, придав матрице проверки четности H следующую форму: ${\begin{bmatrix}-P^{T}|I_{n-k}\end{bmatrix}}$ через базовые операции со строками в GF(2) :

$\mathbf {H} ={\begin{pmatrix}1&1&1&1&0&0\\0&0&1&1&0&1\\1&0&0&1&1&0\\\end{pmatrix}}_{1}\sim {\begin{pmatrix}1&1&1&1&0&0\\0&0&1&1&0&1\\0&1&1&0&1&0\\\end{pmatrix}}_{2}\sim {\begin{pmatrix}1&1&1&1&0&0\\0&1&1&0&1&0\\0&0&1&1&0&1\\\end{pmatrix}}_{3}\sim {\begin{pmatrix}1&1&1&1&0&0\\0&1&1&0&1&0\\1&1&0&0&0&1\\\end{pmatrix}}_{4}.$

Шаг 1: Х.

Шаг 2: Строка 1 добавляется к строке 3.

Шаг 3: Строки 2 и 3 меняются местами.

Шаг 4: Строка 1 добавляется к строке 3.

Отсюда порождающая матрица G может быть получена как ${\begin{bmatrix}I_{k}|P\end{bmatrix}}$ (отмечая, что в частном случае, когда это двоичный код $P=-P$), или конкретно:

$\mathbf {G} ={\begin{pmatrix}1&0&0&1&0&1\\0&1&0&1&1&1\\0&0&1&1&1&0\\\end{pmatrix}}.$

Наконец, умножая все восемь возможных 3-битных строк на G , получаются все восемь допустимых кодовых слов. Например, кодовое слово для битовой строки «101» получается следующим образом:

${\begin{pmatrix}1&0&1\\\end{pmatrix}}\odot {\begin{pmatrix}1&0&0&1&0&1\\0&1&0&1&1&1\\0&0&1&1&1&0\\\end{pmatrix}}={\begin{pmatrix}1&0&1&0&1&1\\\end{pmatrix}}$,

где $\odot$ является символом умножения по модулю 2.

Для проверки пространство строк G ортогонально H , так что $G\odot H^{T}=0$

Битовая строка «101» находится в первых трех битах кодового слова «101011».

Пример кодировщика

LDPC-кодер

Во время кодирования кадра биты входных данных (D) повторяются и распределяются по набору составляющих кодеров. Составляющие кодеры обычно представляют собой аккумуляторы, и каждый аккумулятор используется для генерации символа четности. Единственная копия исходных данных (S _0,K-1 ) передается с битами четности (P) для формирования кодовых символов. Биты S от каждого составного кодера отбрасываются.

Бит четности может использоваться в другом составляющем коде.

В примере с использованием кода DVB-S2 со скоростью 2/3 размер кодированного блока составляет 64800 символов (N=64800) с 43200 битами данных (K=43200) и 21600 битами четности (M=21600). Каждый составной код (проверочный узел) кодирует 16 бит данных, за исключением первого бита четности, который кодирует 8 бит данных. Первые 4680 бит данных повторяются 13 раз (используются в 13 кодах четности), а остальные биты данных используются в 3 кодах четности (нерегулярный код LDPC).

Для сравнения, классические турбокоды обычно используют два составляющих кода, настроенных параллельно, каждый из которых кодирует весь входной блок (K) битов данных. Эти составляющие кодеры представляют собой рекурсивные сверточные коды (RSC) умеренной глубины (8 или 16 состояний), которые разделены перемежителем кода, который чередует одну копию кадра.

В коде LDPC, напротив, параллельно используется множество составных кодов малой глубины (аккумуляторов), каждый из которых кодирует лишь небольшую часть входного кадра. Многие составляющие коды можно рассматривать как множество « сверточных кодов » малой глубины (2 состояния), которые соединены посредством операций повторения и распределения. Операции повторения и распределения выполняют функцию перемежителя в турбокоде.

Возможность более точно управлять связями различных составляющих кодов и уровнем избыточности для каждого входного бита дает большую гибкость при разработке кодов LDPC, что в некоторых случаях может привести к более высокой производительности, чем турбокоды. Турбокоды по-прежнему работают лучше, чем LDPC, при низких скоростях кодирования, или, по крайней мере, для турбокодов проще разрабатывать хорошо работающие коды с низкой скоростью.

На практике оборудование, формирующее аккумуляторы, повторно используется в процессе кодирования. То есть, как только первый набор битов четности сгенерирован и биты четности сохранены, то же самое аппаратное обеспечение аккумулятора используется для генерации следующего набора битов четности.

Декодирование

Как и в случае с другими кодами, с максимальным правдоподобием декодирование кода LDPC в двоичном симметричном канале является NP-полной задачей. показано путем сокращения трехмерного сопоставления . Таким образом, если предположить, что P != NP , что широко распространено, то выполнение оптимального декодирования для произвольного кода любого полезного размера непрактично.

Однако неоптимальные методы, основанные на итеративном декодировании с распространением доверия , дают отличные результаты и могут быть практически реализованы. Методы неоптимального декодирования рассматривают каждую проверку четности, составляющую LDPC, как независимый код одиночной проверки четности (SPC). Каждый код SPC декодируется отдельно с использованием методов soft-in-soft-out (SISO), таких как SOVA , BCJR , MAP и других их производных. Информация мягкого решения от каждого SISO-декодирования перекрестно проверяется и обновляется с помощью других избыточных SPC-декодирований того же информационного бита. Каждый код SPC затем снова декодируется с использованием обновленной информации мягкого решения. Этот процесс повторяется до тех пор, пока не будет получено допустимое кодовое слово или пока декодирование не будет исчерпано. Этот тип декодирования часто называют декодированием суммы произведений.

Декодирование кодов SPC часто называют обработкой «проверочного узла», а перекрестную проверку переменных часто называют обработкой «переменного узла».

В практической реализации декодера LDPC наборы кодов SPC декодируются параллельно для увеличения пропускной способности.

Напротив, распространение убеждений в канале двоичного стирания особенно просто, когда оно состоит из итеративного удовлетворения ограничений.

Например, предположим, что допустимое кодовое слово 101011 из приведенного выше примера передается по каналу двоичного стирания и принимается со стиранием первого и четвертого битов, что дает ?01?11. Поскольку переданное сообщение должно удовлетворять ограничениям кода, сообщение можно представить, записав полученное сообщение в верхней части графа коэффициентов.

В этом примере первый бит еще невозможно восстановить, поскольку все связанные с ним ограничения содержат более одного неизвестного бита. Чтобы приступить к декодированию сообщения, необходимо выявить ограничения, связанные только с одним из стертых битов. В этом примере достаточно только второго ограничения. При рассмотрении второго ограничения выяснилось, что четвертый бит должен быть нулевым, поскольку только ноль в этой позиции удовлетворяет ограничению.

Затем эта процедура повторяется. Новое значение четвертого бита теперь можно использовать в сочетании с первым ограничением для восстановления первого бита, как показано ниже. Это означает, что первый бит должен быть единицей, чтобы удовлетворить крайнему левому ограничению.

Таким образом, сообщение может быть декодировано итеративно. Для других моделей каналов сообщения, передаваемые между узлами переменных и узлами проверки, представляют собой действительные числа , которые выражают вероятности и вероятности доверия.

Этот результат можно проверить, умножив исправленное кодовое слово r на матрицу проверки четности H :

$\mathbf {z} =\mathbf {H\odot r} ={\begin{pmatrix}1&1&1&1&0&0\\0&0&1&1&0&1\\1&0&0&1&1&0\\\end{pmatrix}}\odot {\begin{pmatrix}1\\0\\1\\0\\1\\1\\\end{pmatrix}}={\begin{pmatrix}0\\0\\0\\\end{pmatrix}}.$

Поскольку результатом z ( синдромом ) этой операции является нулевой вектор три × один, результирующее кодовое слово r успешно проверяется.

После завершения декодирования исходные биты сообщения «101» можно извлечь, просмотрев первые 3 бита кодового слова.

Хотя этот пример стирания является иллюстративным, он не показывает использование декодирования с мягким решением или передачи сообщений с мягким решением, которое используется практически во всех коммерческих декодерах LDPC.

Обновление информации об узле

В последние годы Также было проведено много работы по изучению влияния альтернативных графиков обновления узлов переменных и узлов ограничений. Оригинальный метод, который использовался для декодирования кодов LDPC, был известен как лавинная рассылка . Этот тип обновления требовал, чтобы перед обновлением узла переменной необходимо было обновить все узлы ограничений, и наоборот. В более поздней работе Вила Касадо и др. , Были изучены альтернативные методы обновления, при которых узлы переменных обновляются новейшей доступной информацией о контрольных узлах.

Интуиция, лежащая в основе этих алгоритмов, заключается в том, что узлы переменных, значения которых различаются больше всего, — это те, которые необходимо обновить в первую очередь. Высоконадежные узлы, чья величина логарифмического отношения правдоподобия (LLR) велика и существенно не меняется от одного обновления к другому, не требуют обновлений с той же частотой, что и другие узлы, знак и величина которых колеблются более широко. Эти алгоритмы планирования демонстрируют более высокую скорость сходимости и более низкий уровень ошибок, чем те, которые используют лавинную рассылку. Эти более низкие уровни ошибок достигаются благодаря возможности информированного динамического планирования (IDS). Алгоритм преодоления перехвата наборов близких кодовых слов.

При использовании алгоритмов планирования без лавинной рассылки используется альтернативное определение итерации. Для ( n , k ) LDPC-кода со скоростью k / n полная итерация происходит, когда n переменных и n - k узлов ограничений были обновлены, независимо от порядка, в котором они были обновлены.

Построение кода

Для блоков большого размера коды LDPC обычно создаются путем предварительного изучения поведения декодеров. Поскольку размер блока стремится к бесконечности, можно показать, что декодеры LDPC имеют шумовой порог, ниже которого декодирование надежно достигается, а выше которого декодирование не достигается. в просторечии его называют эффектом обрыва . Этот порог можно оптимизировать, найдя наилучшую пропорцию дуг из проверочных узлов и дуг из переменных узлов. Примерный графический подход к визуализации этого порога — диаграмма EXIT .

Построение конкретного LDPC-кода после такой оптимизации делится на два основных типа методов:

• Псевдослучайные подходы
• Комбинаторные подходы

Построение псевдослучайным подходом основано на теоретических результатах, согласно которым для блоков большого размера случайная конструкция обеспечивает хорошую производительность декодирования. В общем, псевдослучайные коды имеют сложные кодеры, но псевдослучайные коды с лучшими декодерами могут иметь простые кодеры. Часто применяются различные ограничения, чтобы гарантировать, что желаемые свойства, ожидаемые при теоретическом пределе бесконечного размера блока, проявляются при конечном размере блока.

Комбинаторные подходы можно использовать для оптимизации свойств кодов LDPC небольшого размера или для создания кодов с помощью простых кодировщиков.

Некоторые коды LDPC основаны на кодах Рида-Соломона , например код RS-LDPC, используемый в стандарте 10 Gigabit Ethernet . По сравнению со случайно генерируемыми кодами LDPC, структурированные коды LDPC, такие как код LDPC, используемый в стандарте DVB-S2 , могут иметь более простое и, следовательно, более дешевое оборудование, в частности, коды, построенные таким образом, что матрица H является циркулянтной матрицей .

Еще одним способом построения кодов LDPC является использование конечной геометрии . Этот метод был предложен Ю. Коу и др. в 2001 году.

По сравнению с турбокодами

Коды LDPC можно сравнить с другими мощными схемами кодирования, например турбокодами . С одной стороны, на производительность турбокодов по BER влияют ограничения низких кодов. Коды LDPC не имеют ограничений по минимальному расстоянию, это косвенно означает, что коды LDPC могут быть более эффективными при относительно больших скоростях кодирования (например, 3/4, 5/6, 7/8), чем турбокоды. Однако коды LDPC не являются полной заменой: турбокоды являются лучшим решением при более низких скоростях кодирования (например, 1/6, 1/3, 1/2).

См. также

Люди

• Ричард Хэмминг
• Клод Шеннон
• Дэвид Джей Си Маккей
• Ирвинг С. Рид
• Майкл Люби

Теория

• Теория графов
• Код Хэмминга
• Код разреженного графа
• Код расширителя

Приложения

• G.hn/G.9960 (Стандарт ITU-T для организации сетей по линиям электропередачи, телефонным линиям и коаксиальному кабелю)
• 802.3an или 10GBASE-T (Ethernet 10 Гбит/с по витой паре)
• CMMB (Китайское мультимедийное мобильное вещание)
• DVB-S2 / DVB-T2 / DVB-C2 (цифровое видеовещание, 2-го поколения)
• ДМБ-Т/Ч (цифровое видеовещание)
• WiMAX (стандарт IEEE 802.16e для микроволновой связи)
• IEEE 802.11n-2009 ( стандарт Wi-Fi )
• ДОКСИС 3.1
• ATSC 3.0 (цифровое наземное вещание в Северной Америке следующего поколения)
• 3GPP (канал передачи данных 5G-NR)

Другие коды приближения к мощности

• Коды фонтанов
• LT-коды
• Онлайн коды
• Коды Раптора
• Коды с повторением и накоплением (класс простых турбокодов)
• Последовательные составные сверточные коды
• Коды Торнадо (коды LDPC, предназначенные для декодирования со стиранием )
• Турбо коды

Коды достижения потенциала

На данный момент существует только один код достижения мощности путем проектирования и проверки.

• Полярные коды

Внешние ссылки

• Знакомство с кодами проверки четности низкой плотности (Сара Дж. Джонсон, 2010 г.)
• Коды LDPC – краткое руководство (Бернхард Лейнер, 2005 г.)
• Коды LDPC (TU Wien). Архивировано 28 февраля 2019 г. на Wayback Machine.
• Маккей, Дэвид Дж. К. (25 сентября 2003 г.). «47. Коды с низкой плотностью проверки четности» . Теория информации, вывод и алгоритмы обучения . Издательство Кембриджского университета. стр. 557–573. ISBN  9780521642989 .
• Гурусвами, Венкатесан (2006). «Итеративное декодирование кодов проверки четности низкой плотности». arXiv : cs/0610022 .
• Коды LDPC: введение (Амин Шокроллахи, 2003 г.)
• Декодирование кодов LDPC для распространения убеждений (Амир Беннатан, Принстонский университет)
• Коды Turbo и LDPC: реализация, моделирование и стандартизация (Университет Западной Вирджинии)
• Теория информации и кодирование (Марко Хеннхёфер, 2011, TU Ilmenau) - коды LDPC обсуждаются на страницах 74–78.
• Коды LDPC и результаты производительности
• Канал DVB-S.2, включая кодирование LDPC (MatLab)
• Исходный код для кодирования, декодирования и моделирования кодов LDPC доступен в различных местах:
  • Двоичные коды LDPC на языке C
  • Двоичные коды LDPC для Python (основной алгоритм на C)
  • Кодер LDPC и декодер LDPC в MATLAB
  • Инструмент быстрого исправления ошибок (AFF3CT) на C++ 11 для быстрого моделирования LDPC.