Фазовая манипуляция

Эта статья о типе цифровой модуляции. Информацию о протоколе шифрования PSK см. в разделе Предварительный общий ключ .

Фазовая манипуляция ( PSK ) — это процесс цифровой модуляции , который передает данные путем изменения (модулирования) фазы постоянной частоты несущей волны . Модуляция осуществляется путем изменения входных сигналов синуса и косинуса в определенное время. Он широко используется для беспроводных локальных сетей , RFID и связи Bluetooth .

Любая схема цифровой модуляции использует конечное число различных сигналов для представления цифровых данных. PSK использует конечное число фаз, каждой из которых присвоен уникальный набор двоичных цифр . Обычно каждая фаза кодирует одинаковое количество битов. Каждый набор битов образует символ , который представлен конкретной фазой. Демодулятор , разработанный специально для набора символов , используемого модулятором, определяет фазу принятого сигнала и отображает его обратно на символ, который он представляет, восстанавливая таким образом исходные данные. Для этого требуется, чтобы приемник мог сравнивать фазу принятого сигнала с опорным сигналом — такая система называется когерентной (и называется CPSK).

Для CPSK требуется сложный демодулятор, поскольку он должен извлекать опорную волну из принятого сигнала и отслеживать ее, чтобы сравнивать с ней каждую выборку. Альтернативно, фазовый сдвиг каждого отправленного символа может быть измерен относительно фазы предыдущего отправленного символа. Поскольку символы кодируются разностью фаз между последовательными выборками, это называется дифференциальной фазовой манипуляцией (DPSK) . DPSK может быть значительно проще в реализации, чем обычная PSK, поскольку это «некогерентная» схема, т. е. нет необходимости в демодуляторе отслеживать опорную волну. Компромисс заключается в том, что он имеет больше ошибок демодуляции.

Введение

Существует три основных класса методов цифровой модуляции, используемых для передачи данных в цифровом виде:

• Амплитудно-сдвиговая манипуляция (ASK)
• Частотная манипуляция (FSK)
• Фазовая манипуляция (PSK)

Все они передают данные путем изменения некоторых аспектов базового сигнала, несущей волны (обычно синусоиды ), в ответ на сигнал данных. В случае PSK фаза изменяется для представления сигнала данных. Существует два основных способа использования фазы сигнала таким образом:

• Рассматривая саму фазу как передачу информации, в этом случае демодулятор должен иметь опорный сигнал для сравнения фазы принятого сигнала; или
• Рассматривая изменение фазы как передачу информации – дифференциальные схемы, некоторые из которых не нуждаются в опорной несущей (в определенной степени).

Удобный метод представления схем PSK — созвездная диаграмма . Это показывает точки на комплексной плоскости , где в этом контексте действительная и мнимая оси называются синфазными и квадратурными осями соответственно из-за их разделения на 90 °. Такое представление на перпендикулярных осях легко реализовать. Амплитуда каждой точки вдоль синфазной оси используется для модуляции косинусоидальной (или синусоидальной) волны, а амплитуда вдоль квадратурной оси — для модуляции синусоидальной (или косинусоидальной) волны. По соглашению, синфазный сигнал модулирует косинус, а квадратурный – синус.

В PSK выбранные точки созвездия обычно располагаются с одинаковым угловым интервалом по кругу . Это обеспечивает максимальное разделение фаз между соседними точками и, следовательно, лучшую устойчивость к искажениям. Они расположены по кругу, чтобы все они могли передаваться с одинаковой энергией. Таким образом, модули комплексных чисел, которые они представляют, будут одинаковыми, а значит, и амплитуды, необходимые для косинусоидальных и синусоидальных волн. Двумя распространенными примерами являются «двоичная фазовая манипуляция» ( BPSK ), в которой используются две фазы, и «квадратурная фазовая манипуляция» ( QPSK ), в которой используются четыре фазы, хотя может использоваться любое количество фаз. Поскольку передаваемые данные обычно являются двоичными, схема PSK обычно разрабатывается с количеством точек созвездия, равным степени двойки.

Двоичная фазовая манипуляция (BPSK)

созвездной диаграммы для BPSK Пример

BPSK (также иногда называемая PRK, фазовая манипуляция или 2PSK) — это простейшая форма фазовой манипуляции (PSK). В нем используются две фазы, разделенные на 180°, поэтому его также можно назвать 2-PSK. Не имеет особого значения, где именно расположены точки созвездия, и на этом рисунке они показаны на реальной оси, под углами 0° и 180°. Таким образом, он обрабатывает самый высокий уровень шума или искажений до того, как демодулятор примет неправильное решение. Это делает его самым надежным из всех PSK. Однако он способен модулировать только со скоростью 1   бит/символ (как показано на рисунке) и поэтому не подходит для приложений с высокой скоростью передачи данных.

При наличии произвольного фазового сдвига, вносимого каналом связи , демодулятор (см., например, петлю Костаса ) не может определить, какая точка созвездия какая. В результате данные часто дифференциально кодируются перед модуляцией.

BPSK функционально эквивалентен модуляции 2-QAM .

Выполнение

Общая форма BPSK соответствует уравнению:

$s_{n}(t)={\sqrt {\frac {2E_{b}}{T_{b}}}}\cos(2\pi ft+\pi (1-n)),\quad n=0,1.$

Это дает две фазы: 0 и π.В конкретной форме двоичные данные часто передаются с помощью следующих сигналов:

$s_{0}(t)={\sqrt {\frac {2E_{b}}{T_{b}}}}\cos(2\pi ft+\pi )=-{\sqrt {\frac {2E_{b}}{T_{b}}}}\cos(2\pi ft)$ для двоичного "0"

$s_{1}(t)={\sqrt {\frac {2E_{b}}{T_{b}}}}\cos(2\pi ft)$ для двоичной «1»

где f — частота базовой полосы.

Следовательно, пространство сигналов может быть представлено единственной базисной функцией

$\phi (t)={\sqrt {\frac {2}{T_{b}}}}\cos(2\pi ft)$

где 1 представлено ${\sqrt {E_{b}}}\phi (t)$ и 0 представлен $-{\sqrt {E_{b}}}\phi (t)$. Это назначение является произвольным.

Такое использование этой базовой функции показано в конце следующего раздела на временной диаграмме сигнала. Самый верхний сигнал представляет собой косинусоидальную волну, модулированную BPSK, которую будет генерировать модулятор BPSK. Битовый поток, вызывающий этот выходной сигнал, показан над сигналом (остальные части этого рисунка относятся только к QPSK). После модуляции сигнал основной полосы будет перемещен в полосу высоких частот путем умножения $\cos(2\pi f_{c}t)$.

Частота битовых ошибок

Коэффициент ошибок по битам (BER) BPSK при аддитивном белом гауссовском шуме (AWGN) можно рассчитать как:

$P_{b}=Q\left({\sqrt {\frac {2E_{b}}{N_{0}}}}\right)$ или $P_{e}={\frac {1}{2}}\operatorname {erfc} \left({\sqrt {\frac {E_{b}}{N_{0}}}}\right)$

Поскольку на символ приходится только один бит, это также коэффициент ошибок символа.

Квадратурная фазовая манипуляция (QPSK)

Созвездная диаграмма для QPSK с кодированием Грея . Каждый соседний символ отличается только на один бит.

Иногда это называют четырехфазной PSK , 4-PSK или 4- QAM . (Хотя основные концепции QPSK и 4-QAM различны, полученные модулированные радиоволны совершенно одинаковы.) QPSK использует четыре точки на диаграмме созвездия, равноудаленные вокруг круга. Имея четыре фазы, QPSK может кодировать два бита на символ, что показано на диаграмме с кодированием Грея для минимизации частоты ошибок по битам (BER), что иногда ошибочно воспринимается как удвоенный BER по сравнению с BPSK.

Математический анализ показывает, что QPSK можно использовать либо для удвоения скорости передачи данных по сравнению с системой BPSK при сохранении той же полосы пропускания сигнала, либо для поддержания скорости передачи данных BPSK, но вдвое уменьшив необходимую полосу пропускания. В этом последнем случае BER QPSK точно такой же, как BER BPSK, и иное мнение является распространенной путаницей при рассмотрении или описании QPSK. Передаваемая несущая может претерпевать множество фазовых изменений.

Учитывая, что каналы радиосвязи выделяются такими агентствами, как Федеральная комиссия по связи, предоставляя заданную (максимальную) полосу пропускания, преимущество QPSK перед BPSK становится очевидным: QPSK передает в два раза большую скорость передачи данных в заданной полосе пропускания по сравнению с BPSK - при том же BER. . Инженерный штраф заключается в том, что передатчики и приемники QPSK более сложны, чем передатчики и приемники для BPSK. Однако благодаря современным электронным технологиям снижение стоимости очень умеренное.

Как и в случае с BPSK, на принимающей стороне возникают проблемы фазовой неоднозначности, и дифференциально-кодированная на практике часто используется QPSK.

Выполнение

Реализация QPSK является более общей, чем реализация BPSK, и также указывает на реализацию PSK более высокого порядка. Запись символов на диаграмме созвездия в терминах синусоидальных и косинусоидальных волн, используемых для их передачи:

$s_{n}(t)={\sqrt {\frac {2E_{s}}{T_{s}}}}\cos \left(2\pi f_{c}t+(2n-1){\frac {\pi }{4}}\right),\quad n=1,2,3,4.$

Это дает четыре фазы π/4, 3π/4, 5π/4 и 7π/4 по мере необходимости.

В результате получается двумерное пространство сигналов с единичными базисными функциями.

${\begin{aligned}\phi _{1}(t)&={\sqrt {\frac {2}{T_{s}}}}\cos \left(2\pi f_{c}t\right)\\\phi _{2}(t)&={\sqrt {\frac {2}{T_{s}}}}\sin \left(2\pi f_{c}t\right)\end{aligned}}$

Первая базисная функция используется как синфазная составляющая сигнала, а вторая — как квадратурная составляющая сигнала.

Следовательно, сигнальное созвездие состоит из 4 точек сигнального пространства.

${\begin{pmatrix}\pm {\sqrt {\frac {E_{s}}{2}}}&\pm {\sqrt {\frac {E_{s}}{2}}}\end{pmatrix}}.$

Коэффициенты 1/2 указывают на то, что общая мощность делится поровну между двумя несущими.

Сравнение этих базисных функций с функциями BPSK ясно показывает, как QPSK можно рассматривать как два независимых сигнала BPSK. Обратите внимание, что точкам сигнального пространства для BPSK не требуется разделять энергию символа (бита) по двум несущим в схеме, показанной на диаграмме созвездия BPSK.

Системы QPSK могут быть реализованы несколькими способами. Ниже показаны основные компоненты конструкции передатчика и приемника.

Концептуальная структура передатчика для QPSK. Поток двоичных данных разделяется на синфазную и квадратурно-фазовую составляющие. Затем они отдельно модулируются на две ортогональные базисные функции. В этой реализации используются две синусоиды. После этого два сигнала накладываются, и результирующий сигнал является сигналом QPSK. Обратите внимание на использование полярного кодирования без возврата к нулю . Эти кодеры могут быть размещены перед источником двоичных данных, но они помещены после них, чтобы проиллюстрировать концептуальную разницу между цифровыми и аналоговыми сигналами, связанными с цифровой модуляцией.

Структура приемника для QPSK. Согласованные фильтры можно заменить корреляторами. Каждое устройство обнаружения использует эталонное пороговое значение, чтобы определить, обнаружено ли 1 или 0.

Вероятность ошибки

Хотя QPSK можно рассматривать как четвертичную модуляцию, проще рассматривать ее как две независимо модулированные квадратурные несущие. При такой интерпретации четные (или нечетные) биты используются для модуляции синфазной составляющей несущей, а нечетные (или четные) биты используются для модуляции квадратурно-фазовой составляющей несущей. BPSK используется на обеих несущих, и их можно демодулировать независимо.

В результате вероятность битовой ошибки для QPSK такая же, как и для BPSK:

$P_{b}=Q\left({\sqrt {\frac {2E_{b}}{N_{0}}}}\right)$

Однако для достижения той же вероятности битовых ошибок, что и BPSK, QPSK использует удвоенную мощность (поскольку два бита передаются одновременно).

Коэффициент ошибок символов определяется следующим образом:

${\begin{aligned}P_{s}&=1-\left(1-P_{b}\right)^{2}\\&=2Q\left({\sqrt {\frac {E_{s}}{N_{0}}}}\right)-\left[Q\left({\sqrt {\frac {E_{s}}{N_{0}}}}\right)\right]^{2}.\end{aligned}}$

Если отношение сигнал/шум велико (что необходимо для практических систем QPSK), вероятность ошибки символа может быть аппроксимирована:

$P_{s}\approx 2Q\left({\sqrt {\frac {E_{s}}{N_{0}}}}\right)=\operatorname {erfc} \left({\sqrt {\frac {E_{s}}{2N_{0}}}}\right)=\operatorname {erfc} \left({\sqrt {\frac {E_{b}}{N_{0}}}}\right)$

Модулированный сигнал показан ниже для короткого сегмента случайного потока двоичных данных. Две несущие волны — это косинусоидальная волна и синусоидальная волна, как показано в приведенном выше анализе пространства сигналов. Здесь биты с нечетными номерами присвоены синфазной составляющей, а биты с четными номерами — квадратурной составляющей (первый бит принимается за номер 1). Общий сигнал – сумма двух компонентов – показан внизу. Скачки фазы можно увидеть, когда PSK меняет фазу каждого компонента в начале каждого битового периода. Только самая верхняя форма сигнала соответствует описанию, данному для BPSK выше.

Временная диаграмма для QPSK. Поток двоичных данных отображается под осью времени. Два компонента сигнала с присвоением им битов показаны вверху, а общий объединенный сигнал — внизу. Обратите внимание на резкие изменения фазы на некоторых границах битового периода.

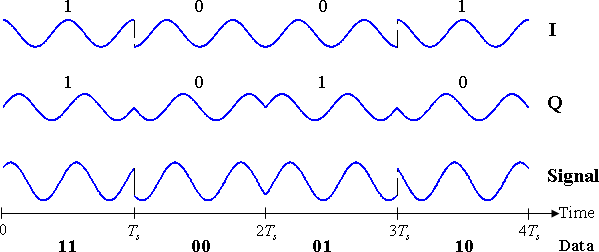
Двоичные данные, передаваемые этим сигналом: 11000110 .

• Нечетные биты, выделенные здесь, вносят вклад в синфазную составляющую: 1 1 0 0 0 1 1 0
• Выделенные здесь четные биты вносят вклад в квадратурную фазовую составляющую: 1 1 0 0 0 1 1 0

Варианты

Смещение QPSK (OQPSK)

Сигнал не проходит через начало координат, поскольку за раз изменяется только один бит символа.

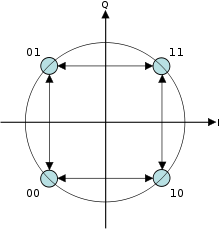
Смещенная квадратурная фазовая манипуляция ( OQPSK ) — это вариант модуляции фазовой манипуляцией, использующий четыре различных значения фазы для передачи. Иногда ее называют шахматной квадратурной фазовой манипуляцией ( SQPSK ).

Разница фазы между QPSK и OQPSK

Одновременный прием четырех значений фазы (два бита ) для построения символа QPSK может позволить фазе сигнала прыгать на целых 180° за раз. Когда сигнал подвергается фильтрованию нижних частот (что типично для передатчика), эти фазовые сдвиги приводят к большим колебаниям амплитуды, что является нежелательным качеством в системах связи. Благодаря смещению синхронизации нечетных и четных битов на один бит-период или половину периода символа синфазная и квадратурная составляющие никогда не будут меняться одновременно. На диаграмме созвездия, показанной справа, видно, что это ограничит фазовый сдвиг не более чем 90° за раз. Это дает гораздо меньшие флуктуации амплитуды, чем QPSK без смещения, и иногда является предпочтительным на практике.

На рисунке справа показана разница в поведении фазы между обычной QPSK и OQPSK. Видно, что на первом графике фаза может измениться сразу на 180°, тогда как в OQPSK изменения никогда не превышают 90°.

Модулированный сигнал показан ниже для короткого сегмента случайного потока двоичных данных. Обратите внимание на смещение на половину периода символа между двумя составляющими волнами. Внезапные фазовые сдвиги происходят примерно в два раза чаще, чем при OQPSK (поскольку сигналы больше не изменяются одновременно), но они менее выражены. Другими словами, величина скачков в OQPSK меньше, чем в QPSK.

Временная диаграмма для смещения QPSK. Поток двоичных данных отображается под осью времени. Два компонента сигнала с присвоением им битов показаны вверху, а общий объединенный сигнал — внизу. Обратите внимание на смещение полупериода между двумя компонентами сигнала.

СОКПСК

Не требующий лицензии по форме QPSK со смещением (SOQPSK) совместим с запатентованным Feher QPSK ( FQPSK ) в том смысле, что детектор QPSK со смещением и интеграцией и сбросом выдает одинаковый выходной сигнал независимо от того, какой тип передатчика используется.

Эти модуляции тщательно формируют формы сигналов I и Q так, что они изменяются очень плавно, и сигнал остается постоянной амплитуды даже во время переходов сигнала. (Вместо того, чтобы мгновенно перемещаться от одного символа к другому или даже линейно, он перемещается плавно по кругу постоянной амплитуды от одного символа к другому.) Модуляцию SOQPSK можно представить как гибрид QPSK и MSK : SOQPSK имеет один и тот же сигнал. созвездия как QPSK, однако фаза SOQPSK всегда стационарна.

Стандартное описание SOQPSK-TG включает троичные символы . SOQPSK — одна из наиболее распространенных схем модуляции, применяемых в спутниковой связи на околоземной орбите .

π /4-QPSK

Диаграмма двойного созвездия для π/4-QPSK. На нем показаны два отдельных созвездия с идентичным кодом Грея, но повернутые на 45° друг относительно друга.

Этот вариант QPSK использует два идентичных созвездия, повернутых на 45° ( $\pi /4$ радианы, отсюда и название) по отношению друг к другу. Обычно для выбора точек из одного из созвездий используются либо четные, либо нечетные символы, а другие символы выбирают точки из другого созвездия. Это также уменьшает фазовые сдвиги с максимального значения 180°, но только до максимального значения 135°, и, таким образом, флуктуации амплитуды $\pi /4$-QPSK находится между OQPSK и QPSK без смещения.

Одним из свойств этой схемы модуляции является то, что если модулированный сигнал представлен в комплексной области, переходы между символами никогда не проходят через 0. Другими словами, сигнал не проходит через начало координат. Это снижает динамический диапазон колебаний сигнала, что желательно при разработке сигналов связи.

С другой стороны, $\pi /4$-QPSK легко поддается демодуляции и был принят, например, для использования в системах TDMA сотовых телефонных .

Модулированный сигнал показан ниже для короткого сегмента случайного потока двоичных данных. Конструкция аналогична описанной выше для обычного QPSK. Последовательные символы взяты из двух созвездий, показанных на схеме. Таким образом, первый символ (1 1) взят из «синего» созвездия, а второй символ (0 0) взят из «зеленого» созвездия. Обратите внимание, что величины двух составляющих волн изменяются при переключении между созвездиями, но общая величина сигнала остается постоянной ( постоянная огибающая ). Фазовые сдвиги находятся между двумя предыдущими временными диаграммами.

Временная диаграмма для π/4-QPSK. Поток двоичных данных отображается под осью времени. Два компонента сигнала с присвоением им битов показаны вверху, а общий объединенный сигнал — внизу. Обратите внимание, что последовательные символы берутся поочередно из двух созвездий, начиная с «синего».

ДПКПСК

Квадратурная фазовая манипуляция с двойной поляризацией (DPQPSK) или QPSK с двойной поляризацией - включает поляризационное мультиплексирование двух разных сигналов QPSK, тем самым улучшая спектральную эффективность в 2 раза. Это экономичная альтернатива использованию 16-PSK. вместо QPSK для удвоения спектральной эффективности.

ПСК высшего порядка

Схема созвездия для 8-PSK с кодировкой Грея

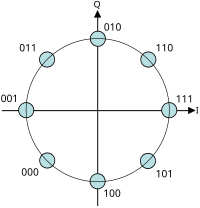
Для построения созвездия PSK может использоваться любое количество фаз, но 8-PSK обычно является развернутым созвездием PSK самого высокого порядка. При наличии более 8 фаз частота ошибок становится слишком высокой, и доступны более качественные, хотя и более сложные, модуляции, такие как квадратурная амплитудная модуляция (QAM). Хотя может использоваться любое количество фаз, тот факт, что совокупность обычно должна иметь дело с двоичными данными, означает, что количество символов обычно представляет собой степень 2, что позволяет использовать целое число битов на символ.

Частота битовых ошибок

Для общей M-PSK не существует простого выражения для вероятности ошибки символа, если $M>4$. К сожалению, его можно получить только

$P_{s}=1-\int _{-\pi /M}^{\pi /M}p_{\theta _{r}}\left(\theta _{r}\right)d\theta _{r},$

где

${\begin{aligned}p_{\theta _{r}}\left(\theta _{r}\right)&={\frac {1}{2\pi }}e^{-2\gamma _{s}\sin ^{2}\theta _{r}}\int _{0}^{\infty }Ve^{-{\frac {1}{2}}\left(V-2{\sqrt {\gamma _{s}}}\cos \theta _{r}\right)^{2}}\,dV,\\V&={\sqrt {r_{1}^{2}+r_{2}^{2}}},\\\theta _{r}&=\tan ^{-1}\left({\frac {r_{2}}{r_{1}}}\right),\\\gamma _{s}&={\frac {E_{s}}{N_{0}}}\end{aligned}}$

и $r_{1}\sim N\left({\sqrt {E_{s}}},{\frac {1}{2}}N_{0}\right)$ и $r_{2}\sim N\left(0,{\frac {1}{2}}N_{0}\right)$ являются гауссовскими случайными величинами .

Кривые частоты битовых ошибок для BPSK, QPSK, 8-PSK и 16-PSK, канала аддитивного белого гауссовского шума

Это можно аппроксимировать для высоких $M$ и высокий $E_{b}/N_{0}$ к:

$P_{s}\approx 2Q\left({\sqrt {2\gamma _{s}}}\sin {\frac {\pi }{M}}\right).$

Вероятность битовой ошибки для $M$-PSK можно определить только тогда, когда известно битовое отображение. Однако при использовании кодирования Грея наиболее вероятная ошибка при переходе от одного символа к другому приводит только к одной битовой ошибке и

$P_{b}\approx {\frac {1}{k}}P_{s}.$

(Использование кодирования Грея позволяет нам аппроксимировать расстояние Ли ошибок как расстояние Хэмминга ошибок в декодированном потоке битов, что легче реализовать аппаратно.)

На графике справа сравниваются коэффициенты ошибок по битам для BPSK, QPSK (которые одинаковы, как отмечалось выше), 8-PSK и 16-PSK. Видно, что модуляции более высокого порядка имеют более высокую частоту ошибок; однако взамен они обеспечивают более высокую скорость передачи исходных данных.

Границы частоты ошибок различных схем цифровой модуляции можно вычислить с применением объединения, привязанного к сигнальному созвездию.

Спектральная эффективность

Полоса пропускания (или спектральная) эффективность схем модуляции M-PSK увеличивается с увеличением порядка модуляции M (в отличие, например, от M-FSK ):

$\rho ={\frac {\log _{2}M}{2}}\quad [({\text{bits}}/{\text{s}})/{\text{Hz}}]$

То же соотношение справедливо и для M-QAM .

Дифференциальная фазовая манипуляция (DPSK)

Дифференциальное кодирование

Основная статья: дифференциальное кодирование

Дифференциальная фазовая манипуляция (DPSK) — это распространенная форма фазовой модуляции, которая передает данные путем изменения фазы несущей волны. Как упоминалось для BPSK и QPSK, существует неоднозначность фазы, если совокупность вращается под действием какого-либо эффекта в канале связи, через который проходит сигнал. Эту проблему можно решить, используя данные для изменения, а не для установки фазы.

Например, в дифференциально-кодированном BPSK двоичная «1» может быть передана путем добавления 180 ° к текущей фазе, а двоичный «0» - путем добавления 0 ° к текущей фазе. Другой вариант DPSK - это симметричная дифференциальная фазовая манипуляция, SDPSK, где кодирование будет +90 ° для «1» и -90 ° для «0».

В дифференциально-кодированной QPSK (DQPSK) фазовые сдвиги составляют 0°, 90°, 180°, -90°, что соответствует данным «00», «01», «11», «10». Этот вид кодирования можно демодулировать так же, как и недифференциальную PSK, но фазовую неоднозначность можно игнорировать. Таким образом, каждый принятый символ демодулируется в один из $M$ точек в созвездии, и компаратор затем вычисляет разность фаз между этим полученным сигналом и предыдущим. Разница кодирует данные, как описано выше. Симметричная дифференциальная квадратурная фазовая манипуляция (SDQPSK) аналогична DQPSK, но кодирование является симметричным, с использованием значений фазового сдвига -135°, -45°, +45° и +135°.

Модулированный сигнал показан ниже как для DBPSK, так и для DQPSK, как описано выше. На рисунке предполагается, что сигнал начинается с нулевой фазы , поэтому в обоих сигналах наблюдается фазовый сдвиг при $t=0$.

Временная диаграмма для DBPSK и DQPSK. Поток двоичных данных находится над сигналом DBPSK. Отдельные биты сигнала DBPSK группируются в пары для сигнала DQPSK, который меняется только каждые T _s = 2 T _b .

Анализ показывает, что дифференциальное кодирование примерно вдвое увеличивает частоту ошибок по сравнению с обычным кодированием. $M$-PSK, но это можно преодолеть лишь небольшим увеличением $E_{b}/N_{0}$. Более того, этот анализ (и графические результаты, приведенные ниже) основаны на системе, в которой единственным искажением является аддитивный белый гауссов шум (AWGN). Однако в системе связи также будет физический канал между передатчиком и приемником. Этот канал, как правило, вносит в сигнал PSK неизвестный фазовый сдвиг; в этих случаях дифференциальные схемы могут обеспечить более высокий коэффициент ошибок, чем обычные схемы, которые полагаются на точную информацию о фазе.

Одним из самых популярных приложений DPSK является стандарт Bluetooth , где $\pi /4$-Реализованы DQPSK и 8-DPSK.

Демодуляция

Сравнение BER между DBPSK, DQPSK и их недифференциальными формами с использованием кодирования Грея и работы в белом шуме

Для сигнала, который был закодирован дифференциально, существует очевидный альтернативный метод демодуляции. Вместо обычной демодуляции и игнорирования неоднозначности фазы несущей, фаза между двумя последовательными полученными символами сравнивается и используется для определения того, какими должны были быть данные. Когда дифференциальное кодирование используется таким образом, эта схема известна как дифференциальная фазовая манипуляция (DPSK). Обратите внимание, что это немного отличается от просто дифференциально кодированной PSK, поскольку при приеме полученные символы не декодируются один за другим в точки совокупности, а вместо этого сравниваются непосредственно друг с другом.

Вызовите полученный символ в $k$^й временной интервал $r_{k}$ и пусть у него есть фаза $\phi _{k}$. Без ограничения общности предположим, что фаза несущей волны равна нулю. Обозначим термин аддитивного белого гауссовского шума (AWGN) как $n_{k}$. Затем

$r_{k}={\sqrt {E_{s}}}e^{j\phi _{k}}+n_{k}.$

Переменная решения для $k-1$^й символ и $k$^й символ представляет собой разность фаз между $r_{k}$ и $r_{k-1}$. То есть, если $r_{k}$ проецируется на $r_{k-1}$, решение принимается по фазе результирующего комплексного числа:

$r_{k}r_{k-1}^{*}=E_{s}e^{j\left(\varphi _{k}-\varphi _{k-1}\right)}+{\sqrt {E_{s}}}e^{j\varphi _{k}}n_{k-1}^{*}+{\sqrt {E_{s}}}e^{-j\varphi _{k-1}}n_{k}+n_{k}n_{k-1}^{*}$

где верхний индекс * обозначает комплексное сопряжение . При отсутствии шума фаза этого равна $\phi _{k}-\phi _{k-1}$, фазовый сдвиг между двумя полученными сигналами, который можно использовать для определения передаваемых данных.

Вероятность ошибки для DPSK в целом рассчитать сложно, но в случае DBPSK она равна:

$P_{b}={\frac {1}{2}}e^{-{\frac {E_{b}}{N_{0}}}},$

что при числовой оценке лишь немного хуже обычного BPSK, особенно при более высоких $E_{b}/N_{0}$ ценности.

Использование DPSK позволяет избежать необходимости использования сложных схем восстановления несущей для обеспечения точной оценки фазы и может быть привлекательной альтернативой обычной PSK.

В оптической связи модулированы по фазе лазера . данные могут быть дифференциально Модуляция представляет собой лазер, излучающий непрерывную волну , и модулятор Маха – Цендера , который принимает электрические двоичные данные. В случае BPSK лазер передает поле без изменений для двоичной «1» и с обратной полярностью для «0». Демодулятор состоит из интерферометра с линией задержки , который задерживает один бит, поэтому можно сравнивать два бита одновременно. При дальнейшей обработке фотодиод преобразует оптическое поле в электрический ток, поэтому информация возвращается в исходное состояние.

Коэффициенты битовых ошибок DBPSK и DQPSK сравниваются с их недифференциальными аналогами на графике справа. Потери при использовании DBPSK достаточно малы по сравнению со снижением сложности, которое часто используется в системах связи, которые в противном случае использовали бы BPSK. Однако для DQPSK потеря производительности по сравнению с обычным QPSK больше, и разработчик системы должен сбалансировать это с уменьшением сложности.

Пример: BPSK с дифференциальным кодированием.

Схема системы дифференциального кодирования/декодирования

На $k^{\textrm {th}}$ временной интервал вызывает бит, который нужно модулировать $b_{k}$, бит дифференциального кодирования $e_{k}$ и результирующий модулированный сигнал $m_{k}(t)$. Предположим, что на диаграмме созвездий символы располагаются на уровне ±1 (что является BPSK). Дифференциальный энкодер производит:

$\,e_{k}=e_{k-1}\oplus b_{k}$

где $\oplus {}$ указывает на двоичное сложение или сложение по модулю 2 .

Сравнение BER между BPSK и BPSK с дифференциальным кодированием, работающим в белом шуме

Так $e_{k}$ меняет состояние (с двоичного «0» на двоичную «1» или с двоичной «1» на двоичный «0»), если $b_{k}$ представляет собой двоичную «1». В противном случае он остается в прежнем состоянии. Это описание дифференциально-кодированной BPSK, приведенное выше.

Полученный сигнал демодулируется для получения $e_{k}=\pm 1$ а затем дифференциальный декодер меняет процедуру кодирования и выдает

$b_{k}=e_{k}\oplus e_{k-1},$

поскольку двоичное вычитание аналогично двоичному сложению.

Поэтому, $b_{k}=1$ если $e_{k}$ и $e_{k-1}$ различаются и $b_{k}=0$ если они одинаковы. Следовательно, если оба $e_{k}$ и $e_{k-1}$ перевернуты ​ , $b_{k}$ все равно будет декодировано правильно. Таким образом, фазовая неоднозначность в 180° не имеет значения.

По аналогичному принципу могут быть разработаны дифференциальные схемы для других модуляций PSK. Формы сигналов для DPSK такие же, как для дифференциально-кодированной PSK, приведенной выше, поскольку единственное изменение между двумя схемами происходит в приемнике.

Кривая BER для этого примера сравнивается с обычной BPSK справа. Как упоминалось выше, хотя частота ошибок увеличивается примерно вдвое, увеличение, необходимое для $E_{b}/N_{0}$ преодолеть это мало. Увеличение $E_{b}/N_{0}$ однако необходимое для преодоления дифференциальной модуляции в кодированных системах значение больше – обычно около 3 дБ. Ухудшение производительности является результатом некогерентной передачи – в данном случае речь идет о том, что отслеживание фазы полностью игнорируется.

Определения

Для математического определения коэффициента ошибок потребуются некоторые определения:

• $E_{b}$, энергия на бит
• $E_{s}=nE_{b}$, энергия на символ с n битами
• $T_{b}$, длительность бита
• $T_{s}$, длительность символа
• ${\frac {1}{2}}N_{0}$, шума спектральная плотность мощности ( Вт / Гц )
• $P_{b}$, вероятность битовой ошибки
• $P_{s}$, вероятность ошибки символа

$Q(x)$ даст вероятность того, что одна выборка, взятая из случайного процесса с функцией плотности вероятности Гаусса с нулевым средним и единичной дисперсией , будет больше или равна $x$. Это масштабированная форма дополнительной функции ошибки Гаусса :

$Q(x)={\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }e^{-{\frac {1}{2}}t^{2}}\,dt={\frac {1}{2}}\operatorname {erfc} \left({\frac {x}{\sqrt {2}}}\right),\ x\geq 0$.

Приведенные здесь коэффициенты ошибок относятся к аддитивному белому гауссовскому шуму (AWGN). Эти коэффициенты ошибок ниже, чем рассчитанные для каналов с замиранием , и, следовательно, являются хорошим теоретическим эталоном для сравнения.

Приложения

Благодаря простоте PSK, особенно по сравнению с ее конкурентом с квадратурной амплитудной модуляцией , она широко используется в существующих технологиях.

Стандарт беспроводной локальной сети IEEE 802.11b-1999 . использует множество различных PSK в зависимости от требуемой скорости передачи данных. При базовой скорости 1   Мбит /с используется DBPSK (дифференциальный BPSK). Для обеспечения расширенной скорости 2   Мбит/с используется DQPSK. Для достижения скорости 5,5   Мбит/с и полной скорости 11   Мбит/с используется QPSK, но он должен сочетаться с дополнительной кодовой манипуляцией . Стандарт высокоскоростной беспроводной локальной сети IEEE 802.11g-2003 . имеет восемь скоростей передачи данных: 6, 9, 12, 18, 24, 36, 48 и 54   Мбит/с. В режимах 6 и 9   Мбит/с используется модуляция OFDM , при которой каждая поднесущая модулируется BPSK. В режимах 12 и 18   Мбит/с используется OFDM с QPSK. Четыре самых быстрых режима используют OFDM с формами квадратурной амплитудной модуляции .

Благодаря своей простоте BPSK подходит для недорогих пассивных передатчиков и используется в стандартах RFID , таких как ISO/IEC 14443 , который был принят для биометрических паспортов , кредитных карт, таких как American Express от ExpressPay , и многих других приложений.

Bluetooth 2 использует $\pi /4$-DQPSK на более низкой скорости (2   Мбит/с) и 8-DPSK на более высокой скорости (3   Мбит/с), когда связь между двумя устройствами достаточно надежна. Bluetooth 1 модулирует с помощью гауссовой манипуляции с минимальным сдвигом , двоичной схемы, поэтому любой выбор модуляции в версии 2 обеспечит более высокую скорость передачи данных. Аналогичная технология IEEE 802.15.4 (стандарт беспроводной связи, используемый Zigbee ) также опирается на PSK с использованием двух частотных диапазонов: 868–915   МГц с BPSK и 2,4   ГГц с OQPSK.

И QPSK, и 8PSK широко используются в спутниковом вещании. QPSK до сих пор широко используется при потоковой передаче спутниковых каналов SD и некоторых каналов HD. Программы высокой четкости передаются почти исключительно в формате 8PSK из-за более высокой скорости передачи данных HD-видео и высокой стоимости спутниковой полосы пропускания. Стандарт DVB-S2 требует поддержки как QPSK, так и 8PSK. Чипсеты, используемые в новых спутниковых приставках, таких как серия Broadcom 7000, поддерживают 8PSK и обратно совместимы со старым стандартом.

голосового диапазона Исторически сложилось так, что синхронные модемы , такие как Bell 201, 208 и 209 и CCITT V.26, V.27, V.29, V.32 и V.34, использовали PSK.

Взаимная информация с аддитивным белым гауссовским шумом

Взаимная информация PSK по каналу AWGN

Взаимная информация PSK может быть оценена в аддитивном гауссовском шуме путем численного интегрирования ее определения. Кривые взаимной информации насыщаются до количества бит, переносимых каждым символом, в пределе бесконечного отношения сигнал/шум. $E_{s}/N_{0}$. Напротив, в пределе малых отношений сигнал/шум взаимная информация приближается к пропускной способности канала AWGN , которая является супремумом среди всех возможных вариантов статистического распределения символов.

При промежуточных значениях отношения сигнал/шум взаимная информация (MI) хорошо аппроксимируется выражением:

${\textrm {MI}}\simeq \log _{2}\left({\sqrt {{\frac {4\pi }{e}}{\frac {E_{s}}{N_{0}}}}}\right).$

Взаимная информация PSK по каналу AWGN обычно ниже, чем у форматов модуляции QAM .

См. также

• Модуляция двоичной смещенной несущей
• Дифференциальное кодирование
• Модуляция – обзор всех схем модуляции.
• Фазовая модуляция (ФМ) – аналоговый эквивалент ФМн.
• Полярная модуляция
• ПСК31
• ПСК63

Ссылки

Обозначения и теоретические результаты в данной статье основаны на материалах, представленных в следующих источниках:

• Проакис, Джон Г. (1995). Цифровые коммуникации . МакГроу Хилл. ISBN  0-07-113814-5 .
• Коуч, Леон В. II (1997). Цифровые и аналоговые коммуникации . Прентис-Холл. ISBN  0-13-081223-4 .
• Хайкин, Саймон (1988). Цифровые коммуникации . Уайли. ISBN  0-471-62947-2 .