Дельта-сигма модуляция

«Сигма-дельта» перенаправляется сюда. Чтобы узнать о женском обществе, см. Сигма Дельта .

Рисунок 1: Полный процесс 1 ^ул. -порядок синхронного ΔΣ АЦП (вверху) и ΔΣ ЦАП (внизу). модуляции ΔΣ Каждый из них содержит петлю отрицательной обратной связи (фигурную скобку), которая выводит новый результат ΔΣM в каждом тактовом цикле, который передается обратно для вычисления следующего результата ΔΣM . Полный процесс преобразования для каждого из них обычно включает пост- фильтрацию для демодуляции и предварительную фильтрацию для удаления псевдонимов и шума. Аналог зеленый. Цифровой — синий. DDC (цифро-цифровой преобразователь) повторно квантовает входной сигнал с высокой разрядности на низкую разрядность.

1-битная синхронная ΔΣ-модуляция (синяя) синусоидальной волны (красная).

Дельта-сигма ( ΔΣ ; или сигма-дельта , ΣΔ ) модуляция - это метод передискретизации для кодирования сигналов в малой разрядности цифровые сигналы с очень высокой частотой дискретизации как часть процесса дельта-сигма аналого-цифровых преобразователей ( АЦП) и цифро-аналоговых преобразователей (ЦАП). Дельта-сигма-модуляция обеспечивает высокое качество за счет использования контура отрицательной обратной связи во время квантования до более низкой разрядности, который непрерывно корректирует ошибки квантования и перемещает шум квантования исходного сигнала на более высокие частоты, значительно превышающие полосу пропускания . Последующая низкочастотная фильтрация для демодуляции легко удаляет этот высокочастотный шум и усреднения по времени , обеспечивая высокую точность амплитуды, которую в конечном итоге можно закодировать как импульсно-кодовую модуляцию (ИКМ).

И АЦП, и ЦАП могут использовать дельта-сигма-модуляцию. Дельта-сигма-АЦП (например, на рис. 1 вверху) кодирует аналоговый сигнал с использованием высокочастотной дельта-сигма-модуляции, а затем применяет цифровой фильтр для его демодуляции в высокоразрядный цифровой выходной сигнал с более низкой частотой дискретизации. Дельта-сигма ЦАП (например, на рис. 1 внизу) кодирует цифровой входной сигнал высокого разрешения в сигнал с более низким разрешением, но с более высокой частотой дискретизации, который затем можно преобразовать в напряжение и сгладить с помощью аналогового фильтра для демодуляции. В обоих случаях временное использование сигнала малой разрядности при более высокой частоте дискретизации упрощает проектирование схемы и использует преимущества эффективности и высокой точности по времени цифровой электроники .

В первую очередь из-за своей экономической эффективности и уменьшенной сложности схемы этот метод нашел все более широкое применение в современных электронных компонентах, таких как ЦАП, АЦП, синтезаторы частоты , импульсные источники питания и контроллеры двигателей . Грубо квантованный выходной сигнал дельта-сигма-АЦП иногда используется непосредственно при обработке сигнала или в качестве представления для хранения сигнала (например, Super Audio CD хранит необработанный выходной сигнал 1-битного дельта-сигма-модулятора).

Хотя эта статья посвящена синхронной модуляции, для квантования которой требуется точная тактовая частота, асинхронная дельта-сигма-модуляция работает без тактовой частоты.

Мотивация

При прямой передаче аналогового сигнала весь шум в системе и передаче добавляется к аналоговому сигналу, снижая его качество. Оцифровка обеспечивает бесшумную передачу, хранение и обработку. Существует множество методов оцифровки.

В АЦП со скоростью Найквиста аналоговый сигнал дискретизируется с относительно низкой частотой дискретизации, чуть превышающей его частоту Найквиста (вдвое выше самой высокой частоты сигнала) и квантуется многоуровневым квантователем для получения многоразрядного цифрового сигнала . Такие методы с более высоким битом напрямую стремятся к точности амплитуды, но требуют чрезвычайно точных компонентов и поэтому могут страдать от плохой линейности.

Преимущества передискретизации

Вместо этого преобразователи с передискретизацией дают результат с меньшей битовой глубиной при гораздо более высокой частоте дискретизации. Это позволяет достичь сопоставимого качества, используя следующие преимущества:

• Более высокая точность времени (обеспечиваемая высокоскоростными цифровыми схемами и высокоточными часами ).
• Более высокая линейность, обеспечиваемая низкоразрядными АЦП и ЦАП (например, 1-разрядный ЦАП, который выдает только два значения точного высокого напряжения и точного низкого напряжения, в принципе, является совершенно линейным).
• Формирование шума : перемещение шума на более высокие частоты выше интересующего сигнала, чтобы его можно было легко удалить с помощью низкочастотной фильтрации .
• Снижены требования к крутизне для аналоговых фильтров нижних частот сглаживания . Фильтры высокого порядка с плоской полосой пропускания обходятся дороже в аналоговой области, чем в цифровой.

Компромисс частоты/разрешения

Еще одним ключевым аспектом передискретизации является компромисс между частотой и разрешением. Децимационный фильтр, установленный после модулятора, не только фильтрует весь дискретизированный сигнал в интересующей полосе (обрезая шум на более высоких частотах), но также уменьшает частоту дискретизации и, следовательно, представимый частотный диапазон сигнала, одновременно увеличивая выборку. амплитудное разрешение. Это улучшение разрешения по амплитуде достигается путем своего рода усреднения битового потока с более высокой скоростью передачи данных.

Улучшение по сравнению с дельта-модуляцией

Дельта-модуляция — это более ранний метод низкобитовой передискретизации, который также использует отрицательную обратную связь , но кодирует только производную сигнала (его дельту ), а не его амплитуду . Результатом является поток меток и пробелов, представляющих движение сигнала вверх или вниз, который необходимо интегрировать для восстановления амплитуды сигнала. Дельта-модуляция имеет ряд недостатков. Дифференциация изменяет спектр сигнала за счет усиления высокочастотного шума, ослабления низких частот, и отбрасываем компонент постоянного тока . Это делает его динамический диапазон и SNR обратно пропорциональными частоте сигнала. Дельта-модуляция страдает от перегрузки по наклону, если сигналы движутся слишком быстро. И он чувствителен к помехам передачи, которые приводят к кумулятивным ошибкам .

Дельта-сигма-модуляция перестраивает интегратор и квантователь дельта-модулятора, так что на выходе передается информация, соответствующая амплитуде входного сигнала, а не только его производной. Преимущество этого также заключается в включении желаемого формирования шума в процесс преобразования, чтобы намеренно перемещать шум квантования на частоты, более высокие, чем сигнал. Поскольку накопленный сигнал ошибки перед квантованием подвергается фильтрованию нижних частот интегратором дельта-сигма модулятора, последующая отрицательная обратная связь его результата квантования эффективно вычитает низкочастотные компоненты шума квантования, оставляя при этом более высокочастотные компоненты шума.

1-битная дельта-сигма модуляция представляет собой модуляцию плотности импульса.

В конкретном случае одноразрядного синхронного ΔΣ АЦП аналоговый сигнал напряжения эффективно преобразуется в частоту импульсов или плотность импульсов, что можно понимать как модуляцию плотности импульсов (PDM). Последовательность положительных и отрицательных импульсов, представляющих биты с известной фиксированной скоростью, очень легко генерировать, передавать и точно восстанавливать в приемнике, при условии, что можно восстановить время и знак импульсов. Учитывая такую ​​последовательность импульсов дельта-сигма модулятора, исходную форму сигнала можно восстановить с достаточной точностью.

Использование PDM в качестве представления сигнала является альтернативой PCM. Альтернативно, высокочастотный PDM может быть позже подвергнут субдискретизации посредством обработки, называемой прореживанием , и повторно квантован для преобразования его в многобитовый код PCM с более низкой частотой дискретизации, ближе к частоте Найквиста интересующей полосы частот.

История и вариации

Основополагающий статья, сочетающая обратную связь с передискретизацией для достижения дельта-модуляции, была написана Ф. де Ягером из Philips Research Laboratories в 1952 году.

«Система интеграции обратной связи» Чарльза Б. Брама: Вся верхняя половина рисунка 1 представляет собой дельта-сигма-модулятор. Блок №10 представляет собой интегратор с двумя входами . В 4-битном аналого-цифровом квантователе для каждого бита используются обозначения «S» (знак), «1», «2» и «4». Каждая буква «F» означает триггер , а каждая «G» — это вентиль, управляемый генератором 110 кГц.

Принцип улучшения разрешения грубого квантователя за счет использования обратной связи, который является основным принципом дельта-сигма-преобразования, был впервые описан в патенте, поданном в 1954 году К. Чапином Катлером из Bell Labs . Он не был назван так до статьи 1962 года. Иносе и др. из Токийского университета , которым пришла в голову идея добавить фильтр на прямой путь дельта-модулятора. Однако Чарльз Б. Брам из United Aircraft Corp. в 1961 г. подал патент «Интегрирующая система обратной связи». с петлей обратной связи, содержащей интегратор с многобитным квантованием, показанный на рисунке 1.

Вули «Эволюция аналого-цифровых преобразователей с передискретизацией». дает больше истории и ссылки на соответствующие патенты. Некоторые возможности изменения (которые могут применяться в различных комбинациях) - это порядок модулятора, разрядность квантователя, способ прореживания и коэффициент передискретизации.

Модулятор высшего порядка

Рисунок 2. Шумовая обратная связь 2. ^nd -модулятор АЦП ΔΣ-порядка.

Шум квантователя можно дополнительно изменить, заменив сам квантователь другим ΔΣ-модулятором. Это создает 2 ^nd модулятор -порядка, который можно переставлять каскадно (рис. 2). Этот процесс можно повторить, чтобы еще больше увеличить заказ.

Пока 1 ^ул. Модуляторы -порядка безусловно стабильны, анализ устойчивости необходимо проводить для модуляторов с шумовой обратной связью более высокого порядка. Альтернативно, конфигурации с прямой связью по шуму всегда стабильны и требуют более простого анализа. ^§6.1

Многобитный квантователь

Модулятор также можно классифицировать по разрядности его квантователя. Квантизатор, который различает N-уровни, называется квантователем log ₂ N бит. Например, простой компаратор имеет 2 уровня, как и 1-битный квантователь; 3-уровневый квантователь называется 1,5-битным квантователем; 4-уровневый квантователь — это 2-битный квантователь; 5-уровневый квантователь называется 2,5-битным квантователем. Квантаторы с более высоким разрядом по своей сути производят меньший шум квантования.

Одна из критических замечаний по поводу 1-битного квантования заключается в том, что достаточное количество дизеринга в контуре обратной связи нельзя использовать , поэтому при некоторых условиях можно услышать искажения (подробнее обсудите в Direct Stream Digital § DSD и PCM ).

Последующее уничтожение

Децимация тесно связана с дельта-сигма-модуляцией, но она отличается от других и выходит за рамки этой статьи. В оригинальной статье 1962 года децимация не описывалась. Первоначально данные с избыточной выборкой отправлялись как есть. Предложение децимировать дельта-сигма-данные с передискретизацией с помощью цифровой фильтрации перед преобразованием их в звук PCM было сделано DJ Гудманом из Bell Labs в 1969 году. чтобы уменьшить сигнал ΔΣ из-за его высокой частоты дискретизации, одновременно увеличивая его разрядность . Децимация может выполняться в отдельном чипе на приемной стороне потока битов дельта-сигма, иногда с помощью специального модуля внутри микроконтроллера . что полезно для взаимодействия с микрофонами PDM MEMS , хотя многие интегральные схемы ΔΣ АЦП включают децимацию. Некоторые микроконтроллеры даже включают в себя как модулятор, так и дециматор.

Прореживающие фильтры, наиболее часто используемые для ΔΣ АЦП, в порядке возрастания сложности и качества:

1. Фильтр скользящего среднего товарного вагона ( простое скользящее среднее или синхрочастота или синк ¹ фильтр): Это самый простой цифровой фильтр, он сохраняет резкую переходную характеристику, но посредственно разделяет полосы частот. и страдает от интермодуляционных искажений . Фильтр можно реализовать, просто подсчитав, сколько выборок в течение большего интервала выборки являются высокими. Статья 1974 года другого исследователя Bell Labs, Дж. К. Кэнди, «Использование колебаний предельного цикла для получения надежных аналого-цифровых преобразователей». был одним из первых примеров этого.
2. Каскадные интеграторно-гребенчатые фильтры : они называются sinc. ^Н фильтры, эквивалентные каскадированию вышеуказанного sinc ¹ фильтровать N раз и менять порядок операций для повышения эффективности вычислений. Фильтры с меньшим значением N проще, быстрее стабилизируются и имеют меньшее затухание в основной полосе частот, в то время как фильтры с более высоким N немного сложнее, стабилизируются медленнее и имеют больший спад в полосе пропускания, но лучше подавляют нежелательный высокочастотный шум. Однако для противодействия нежелательному затуханию в полосе пропускания можно применять компенсационные фильтры. Синк ^Н фильтры подходят для уменьшения сигма-дельта-модуляции до четырехкратного значения частоты Найквиста. Высота первой боковой нагрузки составляет -13·N дБ, а высота последующих лепестков постепенно падает, но только области вокруг нулей будут совпадать с интересующей полосой низких частот; например, при понижении частоты дискретизации на 8 самый большой высокочастотный компонент с наложениями может быть на -16 дБ ниже пика интересующей полосы с синхр. ¹ фильтр, но на -40 дБ ниже для синка ³ фильтр, и если вас интересует только более узкая полоса пропускания, в него будет проникать еще меньше высокочастотных компонентов (см. рисунки 7–9 в статье Лиона).
3. Оконные фильтры sinc-in-time (кирпичная стена по частоте) : хотя sinc функции бесконечная поддержка не позволяет реализовать ее за конечное время , вместо этого функцию sinc можно использовать в оконном режиме для реализации фильтров с конечной импульсной характеристикой . Эта аппроксимированная конструкция фильтра, практически не сохраняя затухания интересующей низкочастотной полосы, по-прежнему удаляет почти весь нежелательный высокочастотный шум. Обратной стороной является низкая производительность во временной области (например, выбросы и пульсации переходной характеристики ), более высокая задержка (т. е. время свертки обратно пропорционально крутизне перехода отсечки) и более высокие вычислительные требования. Они являются фактическим стандартом для высококачественных цифровых аудиоконвертеров.

Снижение шума основной полосы за счет увеличения коэффициента передискретизации и порядка ΔΣM.

Рисунок 3: Вверху: синусоидальный входной сигнал, наложенный на его синхронное представление ΔΣ, созданное с использованием высокого коэффициента передискретизации. В центре: фильтрация представления ΔΣ дает аппроксимацию исходной синусоидальной волны. Внизу: остаточная ошибка ΔΣ АЦП с добавлением дизеринга и без него .

Когда сигнал квантуется, результирующий сигнал можно аппроксимировать добавлением белого шума примерно одинаковой интенсивности по всему спектру. В действительности шум квантования, конечно, не является независимым от сигнала, и эта зависимость приводит к предельным циклам и является источником холостых тонов и структурного шума в дельта-сигма-преобразователях. Однако добавление шума дизеринга (рис. 3) уменьшает такие искажения , делая шум квантования более случайным.

ΔΣ АЦП уменьшают количество этого шума в основной полосе частот , расширяя его и формируя так, чтобы он преимущественно находился на более высоких частотах. Затем его можно легко отфильтровать с помощью недорогих цифровых фильтров без использования высокоточных аналоговых схем, необходимых для АЦП Найквиста.

Передискретизация для распределения шума квантования

Шум квантования в полосе частот модулирующего сигнала (от постоянного тока до $2f_{0}$) можно уменьшить за счет увеличения коэффициента передискретизации (OSR), определяемого формулой

$\mathrm {OSR} \,=\,{\frac {f_{s}}{2f_{0}}}=2^{d}$

где $f_{\mathrm {s} }$ частота дискретизации и $2f_{0}$ - это частота Найквиста (минимальная частота дискретизации, необходимая для предотвращения наложения спектров, которая в два раза превышает максимальную частоту исходного сигнала). $f_{0}$). Поскольку передискретизация обычно выполняется в степени двойки, $d$ показывает, во сколько раз OSR удваивается.

Рисунок 4. Кривые формирования шума и спектр шума в 1. ^ул. , 2 ^nd , и 3 ^р-д -модуляторы ΔΣ-порядка.

Как показано на рисунке 4, общее количество шума квантования одинаково как в преобразователе Найквиста (желтые + зеленые области), так и в преобразователе передискретизации (синие + зеленые области). Но преобразователи с передискретизацией распределяют этот шум в гораздо более широком диапазоне частот. Преимущество состоит в том, что общее количество шума в интересующем диапазоне частот значительно меньше для преобразователей с передискретизацией (только небольшая зеленая область), чем для преобразователя Найквиста (общая площадь желтого + зеленого).

Формирование шума

На рисунке 4 показано, как ΔΣ-модуляция формирует шум для дальнейшего уменьшения количества шума квантования в основной полосе частот в обмен на увеличение шума на более высоких частотах (где его можно легко отфильтровать). Кривые ΔΣ-модуляторов более высокого порядка обеспечивают еще большее снижение шума в основной полосе частот.

Эти кривые получаются с использованием математических инструментов, называемых преобразованием Лапласа (для сигналов с непрерывным временем , например, в контуре модуляции АЦП) или Z-преобразованием (для сигналов с дискретным временем , например, в контуре модуляции ЦАП). Эти преобразования полезны для преобразования более сложных математических вычислений из временной области в более простые математические вычисления в сложной частотной области комплексной переменной. ${\text{s}}=\sigma +j\omega$ (в области Лапласа) или ${\text{z}}=Ae^{j\phi }$ (в z-домене).

Анализ контура модуляции ΔΣ АЦП в области Лапласа

Рисунок 5 представляет собой 1 ^ул. непрерывным временем Контур модуляции АЦП ΔΣ -порядка (из рисунка 1) как линейная, инвариантная ко времени система с в области Лапласа с уравнением:

Рисунок 5: Петля модуляции ΔΣ в области Лапласа. Интегрирование – это умножение на ${\tfrac {1}{\text{s}}}$ и квантование аппроксимируется добавлением шума.

$$[{\text{in}}({\text{s}})-\Delta \Sigma {\text{M}}({\text{s}})]\cdot {\frac {1}{\text{s}}}+{\text{noise}}({\text{s}})=\Delta \Sigma {\text{M}}({\text{s}})\,.$$

Преобразование Лапласа интегрирования функции времени соответствует простому умножению на ${\tfrac {1}{\text{s}}}$ в обозначениях Лапласа. Предполагается, что интегратор является идеальным интегратором, чтобы упростить математику, но реальный интегратор (или аналогичный фильтр) может иметь более сложное выражение.

Процесс квантования аппроксимируется сложением с источником шума ошибки квантования. Часто предполагается, что шум является белым и не зависит от сигнала, хотя, поскольку квантование (обработка сигнала) § Модель аддитивного шума объясняет, что это не всегда верное предположение (особенно для низкобитового квантования).

Поскольку система и преобразование Лапласа линейны, общее поведение этой системы можно проанализировать, отделив то, как она влияет на входные данные, от того, как она влияет на шум: ^§6

$$\Delta \Sigma {\text{M}}_{\text{total}}({\text{s}})=\Delta \Sigma {\text{M}}_{\text{in}}({\text{s}})+\Delta \Sigma {\text{M}}_{\text{noise}}({\text{s}})\,.$$

Фильтр нижних частот на входе

Чтобы понять, как система влияет только на входной сигнал, временно предположим, что шум равен 0:

$$[{\text{in}}({\text{s}})-\Delta \Sigma {\text{M}}_{\text{in}}({\text{s}})]\cdot {\frac {1}{\text{s}}}+0=\Delta \Sigma {\text{M}}_{\text{in}}({\text{s}})\,,$$

которую можно переставить, чтобы получить следующую передаточную функцию :

$${\frac {\Delta \Sigma {\text{M}}_{\text{in}}({\text{s}})}{{\text{in}}({\text{s}})}}={\frac {\tfrac {1}{\text{s}}}{1+{\tfrac {1}{\text{s}}}}}={\frac {1}{{\text{s}}+1}}\,.$$

Эта передаточная функция имеет единственный полюс в точке ${\text{s}}={\text{-1}}$ в комплексной плоскости , поэтому он эффективно действует как 1 ^ул. -заказать фильтр нижних частот на входном сигнале. (Примечание: частоту среза можно настроить по желанию, включив в цикл умножение на константу).

Фильтр верхних частот от шума

Чтобы понять, как система влияет только на шум, вместо этого временно предполагается, что входной сигнал равен 0:

$$[0-\Delta \Sigma {\text{M}}_{\text{noise}}({\text{s}})]\cdot {\frac {1}{\text{s}}}+{\text{noise}}({\text{s}})=\Delta \Sigma {\text{M}}_{\text{noise}}({\text{s}})\,,$$

которую можно переставить, чтобы получить следующую передаточную функцию:

$${\frac {\Delta \Sigma {\text{M}}_{\text{noise}}({\text{s}})}{{\text{noise}}({\text{s}})}}={\frac {1}{1+{\tfrac {1}{\text{s}}}}}={\frac {s}{{\text{s}}+1}}\,.$$

Эта передаточная функция имеет единственный ноль в точке ${\text{s}}=0$ и один полюс на ${\text{s}}={\text{-1}},$ таким образом, система эффективно действует как фильтр верхних частот на шум, который начинается с 0 при постоянном токе , затем постепенно возрастает, пока не достигнет частоты среза, а затем выравнивается.

Анализ синхронного контура ΔΣ модуляции в z-области

Контур модуляции синхронного ΔΣ ЦАП (рис. 6) тем временем находится в дискретном времени, поэтому его анализ проводится в z-области. Он очень похож на приведенный выше анализ в области Лапласа и дает аналогичные кривые. Примечание: много источников ^§6.1 также проанализировать контур модуляции ΔΣ АЦП в z-домене, который неявно рассматривает непрерывный аналоговый вход как сигнал дискретного времени. Это может быть допустимым приближением при условии, что входной сигнал уже имеет ограниченную полосу пропускания и можно предположить, что он не изменяется во временных масштабах, превышающих частоту дискретизации. Это особенно удобно, когда модулятор реализован в виде схемы с переключаемыми конденсаторами , которая работает путем передачи заряда между конденсаторами с тактовыми интервалами.

Рисунок 6: Петля модуляции ΔΣ в z-домене.

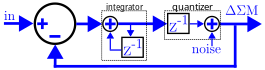
Интегрирование в дискретном времени может представлять собой аккумулятор , который неоднократно суммирует свои входные данные. $x[n]$ с предыдущим результатом его суммирования $y[n]=x[n]+y[n-1].$ Это представлено в z-домене путем обратной передачи выходного сигнала узла суммирования. $y({\text{z}})$ хотя ступень задержки на 1 такт (обозначается как ${\text{z}}^{\text{-1}}$) на другой вход узла суммирования, что дает $y({\text{z}})=x({\text{z}})+y({\text{z}})\cdot {\text{z}}^{\text{-1}}$. Его передаточная функция ${\tfrac {1}{1-{\text{z}}^{\text{-1}}}}$ часто используется для обозначения интеграторов на блок-схемах.

В ΔΣ ЦАП квантователь можно назвать повторным квантователем или цифро-цифровым преобразователем (DDC), поскольку его входной сигнал уже является цифровым и квантованным, но просто преобразуется от цифрового сигнала с более высокой битовой глубиной к более низкому. Это представлено в z-домене другим ${\text{z}}^{\text{-1}}$ последовательный этап задержки с добавлением шума квантования. (Примечание: в некоторых источниках порядок следования мог быть изменен. ${\text{z}}^{\text{-1}}$ и этапы аддитивного шума.)

Уравнение z-области модулятора, представленное как на рисунке 6: $$[{\text{in}}({\text{z}})-\Delta \Sigma {\text{M}}({\text{z}})]\cdot {\frac {1}{1-{\text{z}}^{\text{-1}}}}\cdot {\text{z}}^{\text{-1}}+{\text{noise}}({\text{z}})=\Delta \Sigma {\text{M}}({\text{z}})\,,$$который можно переставить, чтобы выразить выходные данные через входные данные и шум: $$\Delta \Sigma {\text{M}}({\text{z}})={\text{in}}({\text{z}})\cdot {\text{z}}^{\text{-1}}+{\text{noise}}({\text{z}})\cdot (1-{\text{z}}^{\text{-1}})\,.$$Входной сигнал просто выходит из системы с задержкой на один такт. Умножение шумового члена на $(1-{\text{z}}^{\text{-1}})$ представляет собой обратный фильтр первой разности (который имеет один полюс в начале координат и один ноль в начале координат). ${\text{z}}{=}1$) и, таким образом, фильтрует высокочастотный шум.

Модуляторы высшего порядка

Не вдаваясь в математические подробности, ^{(уравнения 8-11)} каскадный $\Theta$ интеграторы для создания $\Theta ^{\text{th}}$Модулятор -order приводит к: $$\Delta \Sigma {\text{M}}_{\Theta }({\text{z}})={\text{in}}({\text{z}})\cdot {\text{z}}^{\text{-1}}+{\text{noise}}({\text{z}})\cdot (1-{\text{z}}^{\text{-1}})^{\Theta }\,.$$Поскольку этот первый разностный обратный фильтр теперь возведен в степень $\Theta$ он будет иметь более крутую кривую формирования шума для улучшения свойств большего затухания в основной полосе частот, поэтому значительно большая часть шума находится над основной полосой частот и может быть легко отфильтрована идеальным фильтром нижних частот.

Теоретическое эффективное количество бит

Теоретическое отношение сигнал/шум (SNR) в децибелах (дБ) для синусоидального входного сигнала, проходящего через $\Theta ^{\text{th}}$-заказать модулятор с $2^{d}$ OSR (и за которым следует идеальный прореживающий фильтр нижних частот) можно математически вывести примерно так: ^{(уравнения 12-21)}

$${\text{SNR}}_{\text{dB}}\approx 3.01\cdot (2\cdot \Theta +1)\cdot d-9.36\cdot \Theta -2.76\,.$$Таким образом, разрешение теоретического эффективного числа битов (ENOB) улучшается за счет ${\textstyle \Theta +{\tfrac {1}{2}}}$ бит при удвоении OSR (увеличение $d$), и ${\textstyle d-{\tfrac {3}{2}}}$ бит при увеличении порядка. Для сравнения, передискретизация АЦП Найквиста (без какого-либо формирования шума) улучшает его ENOB только на ${\tfrac {1}{2}}$ бит за каждое удвоение OSR, что только 1 ⁄ 3 скорости роста ENOB 1 ^ул. -порядок ΔΣM.

Теоретическое соотношение сигнал/шум и ENOB в зависимости от порядка ΔΣM и коэффициента передискретизации (OSR)

	Коэффициент передискретизации					каждое ЛРН удвоение
	2 4 ЛАРН	2 5 ЛАРН	2 6 ЛАРН	2 7 ЛАРН	2 8 ЛАРН
1 ул. -заказ:	24 дБ 3 + 3/4 ​ ​ бита	33 дБ 5 + 1/4 ​ ​ бита	42 дБ 6 + 3/4 ​ бита ​	51 дБ 8 + 1/4 ​ бита ​	60 дБ 9 + 3/4 ​ бита ​	+ 1 + 1 ⁄ 2 бита
2 nd -заказ:	39 дБ 6 + 1/4 ​ ​ бита	54 дБ 8 + 3/4 ​ бита ​	69 дБ 11 + 1/4 ​ ​ бита	84 дБ 13 + 3/4 ​ ​ бита	99 дБ 16 + 1/4 ​ ​ бита	+ 2 + 1 ⁄ 2 бита
3 р-д -заказ:	53 дБ 8 + 3/4 ​ бита ​	75 дБ 12 + 1/4 ​ ​ бита	96 дБ 15 + 3/4 ​ ​ бита	117 дБ 19 + 1/4 ​ ​ бита	138 дБ 22 + 3/4 ​ ​ бита	+ 3 + 1 ⁄ 2 бита
4 й -заказ:	68 дБ 11 + 1/4 ​ ​ бита	95 дБ 15 + 3/4 ​ ​ бита	112 дБ 20 + 1/4 ​ ​ бита	149 дБ 24 + 3/4 ​ ​ бита	177 дБ 29 + 1/2 ​ ​ бита	+ 4 + 1 ⁄ 2 бита
5 й -заказ:	83 дБ 13 + 1/2 ​ ​ бита	116 дБ 19 бит	149 дБ 24 + 1/2 ​ ​ бита	182 дБ 30 бит	215 дБ 35 + 1/2 ​ ​ бита	+ 5 + 1 ⁄ 2 бита
6 й -заказ:	99 дБ 16 бит	137 дБ 22 + 1/2 ​ ​ бита	176 дБ 29 бит	215 дБ 35 + 1/2 ​ ​ бита	254 дБ 42 бита	+ 6 + 1 ⁄ 2 бита
каждый дополнительный заказ:	+ 2 + 1 ⁄ 2 бита	+ 3 + 1 ⁄ 2 бита	+ 4 + 1 ⁄ 2 бита	+ 5 + 1 ⁄ 2 бита	+ 6 + 1 ⁄ 2 бита

Эти точки данных являются теоретическими. На практике в схемах неизбежно возникают другие источники шума, которые ограничивают разрешение, что делает использование ячеек с более высоким разрешением непрактичным.

Связь с дельта-модуляцией

Рисунок 7: Получение дельта-сигмы из дельта-модуляции.

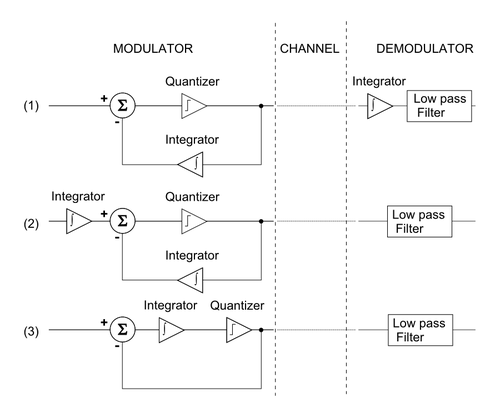
Дельта-сигма-модуляция связана с дельта-модуляцией следующими этапами (рис. 7): ^§6

1. Начните с блок-схемы дельта-модулятора/демодулятора.
2. Свойство линейности интегрирования , ${\textstyle \int a+\int b=\int (a+b)}$, позволяет переместить интегратор, восстанавливающий аналоговый сигнал в секции демодулятора, перед дельта-модулятором.
3. Опять же, свойство линейности интегрирования позволяет объединить два интегратора и получить блок-схему дельта-сигма модулятора/демодулятора.

Если бы квантование было однородным (например, если бы оно было линейным ), вышеизложенное было бы достаточным выводом их гипотетической эквивалентности. Но поскольку квантователь неоднороден , дельта-сигма основана на дельта-модуляции, но они работают по-разному.

Из первой блок-схемы на рисунке 7 интегратор в цепи обратной связи можно убрать, если обратная связь снимается непосредственно со входа фильтра нижних частот. Следовательно, для дельта-модуляции входного сигнала v _в фильтр нижних частот видит сигнал

$\int \operatorname {Quantize} \left({\text{v}}_{\text{in}}-{\text{v}}_{{\text{feedback}}_{\Delta }}\right)dt.\,$

Однако дельта-сигма модуляция того же входного сигнала помещается в фильтр нижних частот.

$\operatorname {Quantize} \left(\int \left({\text{v}}_{\text{in}}-{\text{v}}_{{\text{feedback}}_{\Delta \Sigma }}\right)dt\right).\,$

Другими словами, выполнение дельта-сигма-модуляции вместо дельта-модуляции эффективно поменяло порядок операций интегратора и квантователя. Конечный эффект представляет собой более простую реализацию, которая имеет огромное дополнительное преимущество, заключающееся в формировании шума квантования так, чтобы он находился в основном на частотах выше интересующих сигналов. Этот эффект становится более драматичным при увеличении передискретизации , что позволяет программировать шум квантования. С другой стороны, дельта-модуляция одинаково формирует как шум, так и сигнал.

Кроме того, квантователь (например, компаратор ), используемый в дельта-модуляции, имеет небольшой выходной сигнал, представляющий небольшой шаг вверх и вниз по квантованной аппроксимации входного сигнала, в то время как квантователь, используемый в дельта-сигма, должен принимать значения вне диапазона входного сигнала.

В целом дельта-сигма имеет некоторые преимущества по сравнению с дельта-модуляцией:

• Структура упрощена так
  • нужен только один интегратор,
  • демодулятор может представлять собой простой линейный фильтр (например, RC- или LC-фильтр) для восстановления сигнала, и
  • квантователь (например, компаратор) может иметь полномасштабные выходы.
• Квантованное значение представляет собой интеграл разностного сигнала, который
  • делает его менее чувствительным к скорости изменения сигнала и
  • помогает улавливать низкочастотные компоненты и компоненты постоянного тока.

Пример аналого-цифрового преобразования

Рисунок 8а: Схема простого дельта-сигма-преобразователя.

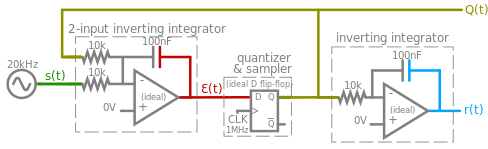
Рисунок 8b: Смоделированное представление ключевых сигналов напряжения во времени. Каждое незначительное вертикальное деление составляет 1 мкс, что соответствует событию выборки тактового сигнала частотой 1 МГц.

Дельта-сигма АЦП различаются по сложности. Приведенная ниже схема представляет собой простой синхронный дельта-сигма АЦП 1-го порядка с двухуровневым квантованием без прореживания.

Упрощенный пример схемы

простая принципиальная схема (рис. 8а) с использованием идеальных элементов Чтобы облегчить понимание, моделируется (напряжения на рис. 8б). Функционально это тот же контур аналогово-цифровой модуляции ΔΣ, что и на рисунке 1 (примечание: инвертирующий интегратор с двумя входами объединяет суммирующий переход и интегратор и дает результат отрицательной обратной связи, а триггер сочетает в себе дискретный квантователь и, что удобно, естественным образом также функционирует как 1-битный ЦАП).

Входной синусоидальный сигнал s(t) частотой 20 кГц преобразуется в 1-битный ШИМ цифровой результат Q(t) . В качестве примера используется частота 20 кГц, поскольку она считается верхним пределом человеческого слуха .

Эту схему можно разместить на макетной плате с недорогими дискретными компонентами (обратите внимание, что в некоторых вариантах используется другое смещение и используются более простые RC-фильтры нижних частот для интеграции вместо операционных усилителей ).

Для простоты D-триггер питается от двух напряжений питания: V _DD = +1 В и V _SS = -1 В, поэтому его двоичный выход Q(t) равен либо +1 В, либо -1 В.

Инвертирующий интегратор с 2 входами

с двумя входами Интегратор инвертирующего операционного усилителя объединяет s(t) с Q(t) для получения Ɛ(t) : $$\varepsilon (t)=-{\frac {1}{RC}}\int (s(t)+Q(t))dt.$$Греческая буква эпсилон используется потому, что Ɛ(t) содержит накопленную ошибку , которая неоднократно исправляется механизмом обратной связи. Хотя оба его входа s(t) и Q(t) изменяются от -1 до 1 вольт, Ɛ(t) вместо этого изменяется всего на пару милливольт около 0 В.

знака интегратора Из-за отрицательного , когда Ɛ(t) в следующий раз производится выборка для получения Q(t) , + Q(t) в этом интеграле фактически представляет собой отрицательную обратную связь от предыдущего тактового цикла.

Квантизатор и триггер сэмплера

Идеальный D-триггер производит выборку Ɛ(t) с тактовой частотой 1 МГц . Представление осциллографа (рис. 8b) имеет второстепенное деление, равное периоду выборки 1 мкс, поэтому каждое второстепенное деление соответствует событию выборки. Поскольку триггер считается идеальным, он рассматривает любое входное напряжение, превышающее 0 В, как высокий логический уровень, а любое входное напряжение меньше 0 В — как низкий логический уровень, независимо от того, насколько оно близко к 0 В (игнорируя проблемы выборки). и-нарушения времени удержания и метастабильность ).

Всякий раз, когда происходит событие выборки:

• если Ɛ(t) выше порога 0 В, то Q(t) станет высоким (+1 В), или
• если Ɛ(t) ниже порога 0 В, то Q(t) станет низким (-1 В).

Q(t) отправляется в качестве результирующего выходного сигнала ШИМ, а также возвращается обратно в инвертирующий интегратор с двумя входами.

Демодуляция

Самый правый интегратор выполняет цифро-аналоговое преобразование Q(t) для получения демодулированного аналогового выходного сигнала r(t) , который восстанавливает исходный синусоидальный входной сигнал в виде кусочно-линейных диагональных сегментов. Хотя r(t) выглядит грубым при такой 50-кратной частоте передискретизации, r(t) можно подвергнуть фильтру нижних частот, чтобы изолировать исходный сигнал. Поскольку частота дискретизации увеличивается относительно максимальной частоты входного сигнала, r(t) будет более точно приближаться к исходному входному сигналу s(t) .

Цифро-аналоговое преобразование

Стоит отметить, что если прореживание никогда не происходило, цифровое представление 1-битного дельта-сигма-модулятора представляет собой просто ШИМ-сигнал, который можно легко преобразовать в аналоговый с помощью фильтра нижних частот , такого же простого, как резистор и конденсатор .

Однако, как правило, дельта-сигма ЦАП преобразует временного ряда дискретный сигнал цифровых выборок с высокой битовой глубиной в сигнал с низкой битовой глубиной (часто 1 бит), обычно с гораздо более высокой частотой дискретизации. Этот дельта-модулированный сигнал затем может быть точно преобразован в аналоговый (поскольку ЦАП с меньшей разрядностью легче обеспечить высокую линейность), который затем проходит недорогую фильтрацию нижних частот в аналоговой области для удаления высокочастотного шума квантования, свойственного Процесс дельта-сигма модуляции.

Повышение дискретизации

Основная статья: Повышение дискретизации § Разработка интерполяционного фильтра

Как объясняют статьи о дискретном преобразовании Фурье и преобразовании Фурье с дискретным временем , периодически дискретизируемый сигнал по своей сути содержит множество более высокочастотных копий или «образов» сигнала. Часто желательно удалить эти высокочастотные изображения перед выполнением фактического этапа дельта-сигма-модуляции, чтобы облегчить требования к возможному аналоговому фильтру нижних частот. Это можно сделать путем повышения дискретизации с использованием интерполяционного фильтра и часто является первым шагом перед выполнением дельта-сигма-модуляции в ЦАП. Повышение дискретизации тесно связано с дельта-сигма-ЦАП, но не является строго частью фактического этапа дельта-сигма-модуляции (аналогично тому, как прореживание тесно связано с дельта-сигма-АЦП, но также не является строго частью дельта-сигма-модуляции), а подробности выходит за рамки данной статьи.

Цифро-цифровая дельта-сигма модуляция

Контур модуляции на рисунке 6 в § Формирование шума можно легко составить с помощью базовых цифровых элементов: вычитателя для разности, аккумулятора для интегратора и младшего разрядного регистра для квантования, который переносит самый старший бит. (s) от интегратора в качестве обратной связи для следующего цикла.

Многоступенчатое формирование шума

Это просто 1 ^ул. Модуляцию -порядка можно улучшить путем каскадного соединения двух или более аккумуляторов с переполнением, каждый из которых эквивалентен единице. ^ул. -заказать дельта-сигма модулятор. Результирующее многоступенчатое формирование шума (MASH). Структура имеет более крутое свойство формирования шума , поэтому обычно используется в цифровом аудио. Выходные сигналы переноса объединяются посредством суммирования и задержек для получения двоичного выходного сигнала, ширина которого зависит от количества этапов (порядка) MASH. Помимо функции формирования шума, он имеет еще два привлекательных свойства:

• просто реализовать аппаратно; только общие цифровые блоки, такие как аккумуляторы , сумматоры и D-триггеры. требуются
• безусловно стабильный (нет контуров обратной связи вне аккумуляторов)

Мы

Техника была впервые представлена ​​в начале 1960-х годов профессором Ясухико Ясудой, когда он был студентом Токийского университета . Название дельта-сигма происходит непосредственно от присутствия дельта-модулятора и интегратора, впервые введенных Иноузом и др. в их патенте приложение. То есть название происходит от интегрирования или суммирования разностей , которые в математике представляют собой операции, обычно связанные с греческими буквами сигма и дельта соответственно.

В 1970-х годах инженеры Bell Labs использовали термин «сигма-дельта», потому что прецедент заключался в том, чтобы называть варианты дельта-модуляции прилагательными, предшествующими слову «дельта», а редактор журнала Analog Devices в 1990 году обосновал, что функциональная иерархия представляет собой «сигма-дельта». ", потому что он вычисляет интеграл от разницы.

Оба названия сигма-дельта и дельта-сигма часто используются.

Асинхронная дельта-сигма модуляция

Рисунок 9: 1-битная асинхронная ΔΣ-модуляция создает выходной сигнал ШИМ (синий на нижнем графике), который вычитается из входного сигнала (зеленый на верхнем графике) для формирования сигнала ошибки (синий на верхнем графике). Эта ошибка интегрирована (пурпурный цвет в середине графика). Когда интеграл ошибки превышает пределы (верхняя и нижняя серые линии на среднем графике), выход ШИМ меняет состояние.

Кирккерт и Миллер опубликовали вариант непрерывного времени под названием «Асинхронная дельта-сигма-модуляция» (ADSM или ASDM) в 1975 году, в котором используется либо триггер Шмитта (т.е. компаратор с гистерезисом ), либо (как утверждается в статье, это эквивалентно) компаратор с фиксированной задержкой. .

В примере на рисунке 9, когда интеграл ошибки превышает допустимые пределы, выходной сигнал меняет состояние, создавая выходную волну с широтно-импульсной модуляцией (ШИМ).

Информация об амплитуде преобразуется без шума квантования во временную информацию выходного ШИМ. Чтобы преобразовать эту непрерывную ШИМ в дискретную, ШИМ может быть дискретизирована преобразователем время-цифра, ограниченное разрешение которого добавляет шум, который может быть сформирован путем обратной подачи.

См. также

• Широтно-импульсная модуляция
• Дельта-модуляция с плавным изменением наклона
• Усилитель класса D (иногда использовать дельта-сигма модуляцию)

Дальнейшее чтение

• Уолт Кестер (октябрь 2008 г.). «Архитектура АЦП III: основы сигма-дельта АЦП» (PDF) . Аналоговые устройства . Проверено 2 ноября 2010 г.
• Р. Джейкоб Бейкер (2009). Проектирование КМОП-схем смешанных сигналов (2-е изд.). Вайли-IEEE. ISBN  978-0-470-29026-2 .
• Р. Шрайер; Г. Темес (2005). Общие сведения о преобразователях дельта-сигма данных . Уайли. ISBN  978-0-471-46585-0 .
• С. Норсуорси; Р. Шрайер; Г. Темес (1997). Преобразователи данных дельта-сигма . Уайли. ISBN  978-0-7803-1045-2 .
• Дж. Кэнди; Г. Темес (1992). Преобразователи данных дельта-сигма с передискретизацией . ISBN  978-0-87942-285-1 .
• Чен, Вэй (2013). Асинхронные сигма-дельта-модуляторы для преобразования данных (PDF) (кандидатская диссертация). Имперский колледж Лондона . дои : 10.25560/23651 . Проверено 19 января 2024 г.

Внешние ссылки

• 1-битные аналого-цифровые и цифро-аналоговые преобразователи, заархивировано 25 февраля 2021 г. на Wayback Machine.
• Сигма-дельта-методы расширяют статью о разрешении ЦАП Тима Уэскотта, 23 июня 2004 г.
• Учебное пособие по проектированию дельта-сигма модуляторов: часть I и часть II, автор Минглианг (Майкл) Лю
• Публикации Gabor Themes
• Учебное пособие по сигма-дельта-модуляции, часть II. Содержит блок-схемы, код и простые пояснения.
• Пример модели Simulink и сценариев для сигма-дельта АЦП непрерывного времени. Содержит пример кода Matlab и модели Simulink.
• Проекты преобразователей дельта-сигма Брюса Вули
• Введение в дельта-сигма-преобразователи (охватывает как сигма-дельта-АЦП, так и ЦАП)
• Демистификация сигма-дельта АЦП . В этой подробной статье рассматривается теория аналого-цифрового преобразователя Delta-Sigma.
• Однобитное дельта-сигма цифро-аналоговое преобразование. Часть I: Теоретическая статья Рэнди Йейтса, представленная на конференции comp.dsp 2004 года.
• Структура MASH (Multi-StAge Noise SHaping) с теоретической и блочной реализацией MASH.
• В архитектуре схемы фильтра формирования шума сигма-дельта АЦП непрерывного времени обсуждаются архитектурные компромиссы для фильтров формирования шума сигма-дельта непрерывного времени.
• Дельта-сигма-конвертеры: модуляция – интуитивно понятное объяснение того, почему работает дельта-сигма-модулятор.
• Цифровой акселерометр с управлением по обратной связи с использованием сигма-дельта модуляции
• Учебное пособие по сигма-дельта АЦП Analog Devices (интерактивное)