Граф Мерингера
Эта статья предоставляет недостаточный контекст для тех, кто не знаком с предметом . ( Апрель 2021 г. ) |
| Граф Мерингера | |
|---|---|
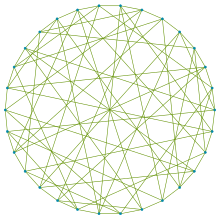 | |
| Назван в честь | Маркус Мерингер |
| Вершины | 30 |
| Края | 75 |
| Радиус | 3 |
| Диаметр | 3 |
| Обхват | 5 |
| Автоморфизмы | 96 |
| Хроматическое число | 3 |
| Хроматический индекс | 5 |
| Характеристики | Клетка |
| Таблица графиков и параметров | |
В математической области теории графов граф Мерингера — это 5- правильный неориентированный граф с 30 вершинами и 75 ребрами, названный в честь Маркуса Мерингера. [1] [2]
Это один из четырех графов (5,5)-клеток , остальные — клетка Фостера , граф Робертсона-Вегнера и граф Вонга .
Он имеет хроматическое число 3, диаметр 3 и 5 -вершинно связен .
Алгебраические свойства
[ редактировать ]Характеристический полином графа Мерингера равен
Ссылки
[ редактировать ]- ^ Вайсштейн, Эрик В. «График Мерингера» . Математический мир .
- ^ Мерингер, Маркус (1999), «Быстрое создание регулярных графов и построение клеток», Journal of Graph Theory , 30 (2): 137–146, doi : 10.1002/(SICI)1097-0118(199902)30:2< 137::AID-JGT7>3.0.CO;2-G , MR 1665972 .
