Алгоритм Марзулло

Алгоритм Марзулло , изобретенный Китом Марзулло для защиты докторской диссертации. диссертация в 1984 году представляет собой алгоритм согласования, используемый для выбора источников для оценки точного времени из ряда зашумленных источников времени. Его усовершенствованная версия, переименованная в « алгоритм пересечения », является частью современного протокола сетевого времени . Алгоритм Марзулло также используется для вычисления расслабленного пересечения n блоков (или, в более общем смысле, n подмножеств R ^н), как того требуют несколько робастных методов оценки набора .

Цель

Алгоритм Марзулло эффективен с точки зрения времени для получения оптимального значения из набора оценок с доверительными интервалами , где фактическое значение может находиться за пределами доверительного интервала для некоторых источников. В этом случае наилучшей оценкой считается наименьший интервал, соответствующий наибольшему числу источников.

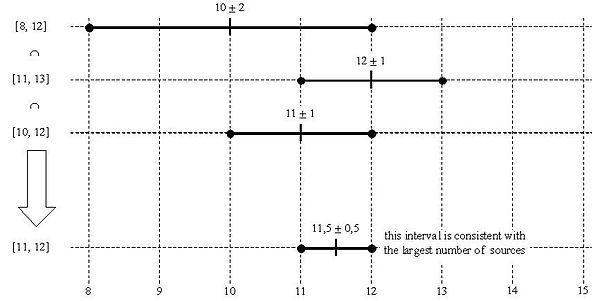
Если у нас есть оценки 10 ± 2, 12 ± 1 и 11 ± 1, то эти интервалы — это [8,12], [11,13] и [10,12], которые пересекаются, образуя [11,12] или 11,5 ± 0,5. как согласующийся со всеми тремя ценностями.

Если вместо этого диапазоны — [8,12], [11,13] и [14,15], то не существует интервала, соответствующего всем этим значениям, но [11,12] соответствует наибольшему количеству источников, а именно двум из них.

Наконец, если диапазоны [8,9], [8,12] и [10,12], то оба интервала [8,9] и [10,12] соответствуют наибольшему количеству источников.

Эта процедура определяет интервал. Если желаемый результат — лучшее значение из этого интервала, то наивным подходом было бы принять в качестве значения центр интервала, как это было указано в исходном алгоритме Марзулло. Более сложный подход позволил бы признать, что это может привести к выбрасыванию полезной информации из доверительных интервалов источников и что вероятностная модель источников может возвращать значение, отличное от центра.

Обратите внимание, что вычисленное значение, вероятно, лучше описать как «оптимистическое», а не «оптимальное». Например, рассмотрим три интервала [10,12], [11, 13] и [11,99,13]. Алгоритм, описанный ниже, вычисляет [11,99, 12] или 11,995 ± 0,005, что является очень точным значением. Если мы подозреваем, что одна из оценок может быть неверной, то по крайней мере две оценки должны быть правильными. При этом условии наилучшая оценка — это [11,13], поскольку это самый большой интервал, который всегда пересекает хотя бы две оценки. Описанный ниже алгоритм легко параметризуется с максимальным количеством неверных оценок.

Метод

Алгоритм Марзулло начинается с подготовки таблицы источников, ее сортировки и последующего поиска (эффективного) пересечения интервалов. Для каждого источника существует диапазон [c−r,c+r], определяемый c ± r. Для каждого диапазона таблица будет иметь два кортежа вида ⟨offset,type⟩ . Один кортеж будет представлять начало диапазона, отмеченного типом -1 как ⟨c-r,-1⟩, а другой будет представлять конец диапазона с типом +1 как ⟨c+r,+1⟩ .

В описании алгоритма используются следующие переменные: best (наибольшее количество найденных перекрывающихся интервалов), cnt (текущее количество перекрывающихся интервалов), beststart и bestend (начало и конец найденного лучшего интервала), i (индекс). и таблица кортежей.

Постройте таблицу кортежей.
Отсортируйте таблицу по смещению. (Если существуют два кортежа с одинаковым смещением, но противоположными типами, что указывает на то, что один интервал заканчивается одновременно с началом другого, то необходим метод определения того, какой из них наступит первым. Такое явление можно рассматривать как перекрытие без продолжительности, которую можно найти по алгоритму, поставив тип -1 перед типом +1. Если такие патологические совпадения считаются нежелательными, их можно избежать, поставив в этом случае тип +1 перед -1.)
[инициализировать] best=0 cnt=0
[цикл] пройти по каждому кортежу в таблице в порядке возрастания

[текущее количество перекрывающихся интервалов] cnt=cnt-type[i]
если cnt>best, то best=cnt beststart=offset[i] bestend=offset[i+1]

комментарий: следующий кортеж в [i+1] будет либо концом интервала (type=+1), и в этом случае он заканчивает этот лучший интервал, либо началом интервала (type=-1 ) и на следующем этапе заменим best.

двусмысленность: не указано, что делать, если best=cnt. Это условие ничьей для наибольшего перекрытия. Можно принять решение либо взять меньшее из значений bestend-beststart и offset[i+1]-offset[i], либо просто взять произвольную одну из двух одинаково хороших записей. Это решение актуально только тогда, когда type[i+1]=+1.

[конечный цикл] возвращает [beststart,bestend] как оптимальный интервал. Количество ложных источников (тех, которые не перекрывают возвращаемый оптимальный интервал) равно количеству источников минус значение лучшего.

Эффективность

Алгоритм Марзулло эффективен как в пространстве, так и во времени. Использование асимптотического пространства равно O(n) , где n — количество источников. Принимая во внимание асимптотическое требование времени, можно считать, что алгоритм состоит из построения таблицы, ее сортировки и поиска. Сортировка может выполняться за время O(n log n), и это доминирует над этапами построения и поиска, которые могут выполняться за линейное время. Следовательно, временная эффективность алгоритма Марзулло равна O(n log n) .

После того как таблица построена и отсортирована, можно обновлять интервал для одного источника (при поступлении новой информации) в линейном времени. Следовательно, обновление данных для одного источника и поиск наилучшего интервала можно выполнить за время O(n).

Ссылки

Марзулло, штат Калифорния (февраль 1984 г.). Поддержание времени в распределенной системе: пример слабосвязанного распределенного сервиса . доктор философии диссертация (Thesis). Кафедра электротехники. Стэнфордский университет. АСИН B000710CSC . ОСЛК 38621764 . ДДК 3781.1984 М.

Внешние ссылки

Миллс, Дэвид Л. (5 августа 2000 г.). «Краткая история времени NTP: признания интернет-хронометриста» (PDF) . ЕЭКИС . УДЕЛ.
«Кит Марзулло» . CSE UCSD