Расслабленный перекресток

Расслабленное пересечение m множеств соответствует классическомупересечение между наборами, за исключением того, что разрешено ослаблять несколько наборов, чтобы избежать пустого пересечения.Это понятие можно использовать для решения задач удовлетворения ограничений. которые являются непоследовательными из-за ослабления небольшого количества ограничений .Когда подход с ограниченной ошибкой рассматривается для оценки параметров ,расслабленное пересечение позволяет быть устойчивым в отношениинекоторым выбросам .

Определение

пересечение q -релаксированное m подмножеств $X_{1},\dots ,X_{m}$из $R^{n}$,обозначается $X^{\{q\}}=\bigcap ^{\{q\}}X_{i}$это совокупность всех $x\in R^{n}$которые принадлежат всем $X_{i}$'s, кроме $q$самое большее.Это определение иллюстрируется рисунком 1.

Рисунок 1. q -пересечение 6 наборов для q =2 (красный), q =3 (зеленый), q =4 (синий), q =5 (желтый).

Определять $\lambda (x)={\text{card}}\left\{i\ |\ x\in X_{i}\right\}.$

У нас есть $X^{\{q\}}=\lambda ^{-1}([m-q,m]).$

Таким образом, характеристика q-релаксированного пересечения представляет собой задачу обращения множества .

Пример

Рассмотрим 8 интервалов: $X_{1}=[1,4],$$X_{2}=\ [2,4],$$X_{3}=[2,7],$$X_{4}=[6,9],$$X_{5}=[3,4],$$X_{6}=[3,7].$

У нас есть

$X^{\{0\}}=\emptyset ,$$X^{\{1\}}=[3,4],$$X^{\{2\}}=[3,4],$$X^{\{3\}}=[2,4]\cup [6,7],$$X^{\{4\}}=[2,7],$$X^{\{5\}}=[1,9],$$X^{\{6\}}=]-\infty ,\infty [.$

Расслабленное пересечение интервалов

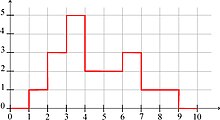
Расслабленное пересечение интервалов не обязательно является интервалом. Таким образом, мы принимаеминтервальная оболочка результата. Если $X_{i}$это интервалы, расслаблениепересечение можно вычислить со сложностью m .log( m ), используя Алгоритм Марзулло . Этого достаточно, чтобыотсортировать все нижние и верхние границы интервалов m, чтобы представитьфункция $\lambda$. Тогда мы легко получаем набор

$X^{\{q\}}=\lambda ^{-1}([m-q,m])$

что соответствует объединению интервалов.Затем мы возвращаемнаименьший интервал, содержащий это объединение.

На рисунке 2 показана функция $\lambda (x)$связанный с предыдущим примером.

Рисунок 2. Функция членства в множестве, связанная с 6 интервалами.

Расслабленное пересечение коробок

Чтобы вычислить q -релаксированное пересечение m блоков $R^{n}$, мы проецируем все m блоков относительно осей n .Для каждой из n групп по m интервалов мы вычисляем q -релаксированное пересечение.Мы возвращаем декартово произведение n полученных интервалов. На рисунке 3 представлениллюстрация 4-расслабленного пересечения 6 ящиков. Каждая точкакрасный ящик принадлежит 4 из 6 ящиков.

Рисунок 3. Красный прямоугольник соответствует 4-релаксированному пересечению 6 прямоугольников.

Расслабленный союз

объединение q -релаксированное $X_{1},\dots ,X_{m}$ определяется

${\overset {\{q\}}{\bigcup }}X_{i}=\bigcap ^{\{m-1-q\}}X_{i}$

Обратите внимание, что когда q = 0, расслабленное объединение/пересечение соответствуетклассический союз/пересечение. Точнее, мы имеем

$\bigcap ^{\{0\}}X_{i}=\bigcap X_{i}$

и

${\overset {\{0\}}{\bigcup }}X_{i}=\bigcup X_{i}$

Закон де Моргана

Если ${\overline {X}}$ обозначает дополнительный набор $X_{i}$, у нас есть

${\overline {\bigcap ^{\{q\}}X_{i}}}={\overset {\{q\}}{\bigcup }}{\overline {X_{i}}}$

${\overline {{\overset {\{q\}}{\bigcup }}X_{i}}}=\bigcap ^{\{q\}}{\overline {X_{i}}}.$

Как следствие

${\overline {\bigcap \limits ^{\{q\}}X_{i}}}={\overline {{\overset {\{m-q-1\}}{\bigcup }}X_{i}}}=\bigcap ^{\{m-q-1\}}{\overline {X_{i}}}$

Расслабление подрядчиков

Позволять $C_{1},\dots ,C_{m}$ быть подрядчиками для съемок $X_{1},\dots ,X_{m}$,затем

$C([x])=\bigcap ^{\{q\}}C_{i}([x]).$

является подрядчиком по $X^{\{q\}}$и

${\overline {C}}([x])=\bigcap ^{\{m-q-1\}}{\overline {C}}_{i}([x])$

является подрядчиком по ${\overline {X}}^{\{q\}}$, где

${\overline {C}}_{1},\dots ,{\overline {C}}_{m}$

являются подрядчиками для

${\overline {X}}_{1},\dots ,{\overline {X}}_{m}.$

В сочетании с алгоритмом ветвей и границ, таким как SIVIA (инверсия множеств посредством интервального анализа), q -расслабленныйпересечение m подмножеств $R^{n}$ можно вычислить.

Приложение к оценке ограниченной ошибки

-релаксированное пересечение q можно использовать для надежной локализации. или для отслеживания.

Надежные наблюдатели также могут быть реализованы с использованием расслабленных пересечений, чтобы быть устойчивыми к выбросам.

Мы предлагаем здесь простой пример для иллюстрации метода.Рассмотрим модель, выход i -й модели которой определяется выражением

$f_{i}(p)={\frac {1}{\sqrt {2\pi p_{2}}}}\exp(-{\frac {(t_{i}-p_{1})^{2}}{2p_{2}}})$

где $p\in R^{2}$. Предположим, что мы имеем

$f_{i}(p)\in [y_{i}]$

где $t_{i}$ и $[y_{i}]$ приведены следующим списком

$\{(1,[0;0.2]),(2,[0.3;2]),(3,[0.3;2]),(4,[0.1;0.2]),(5,[0.4;2]),(6,[-1;0.1])\}$

Наборы $\lambda ^{-1}(q)$ для разных $q$ изображены наРисунок 4.

Рисунок 4. Набор всех векторов параметров, соответствующих ровно 6-q столбцам данных (окрашенным красным), для q = 1,2,3,4,5.