Граф Госсета

Граф Госсета
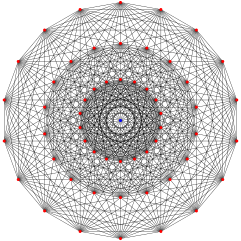Граф Госсета
	Граф Госсета (3 21 ) ; (Имеется 3 кольца по 18 вершин, причем в центре этой проекции совпадают две вершины. С этой проекцией совпадают и ребра.)
Назван в честь	Торольд Госсет
Вершины	56
Края	756
Радиус	3
Диаметр	3
Обхват	3
Автоморфизмы	2903040
Характеристики	Дистанционно-регулярный граф ; Интеграл ; Вершинно-транзитивный
	Таблица графиков и параметров

Граф Госсета , названный в честь Торольда Госсета , представляет собой специфический регулярный граф (1- скелет 7-мерного 3 ₂₁ многогранника ) с 56 вершинами и валентностью 27. ^[1]

Строительство

Граф Госсета можно явно построить следующим образом: 56 вершин — это векторы из R ⁸ получается перестановкой координат и, возможно, взятием противоположного вектора (3, 3, −1, −1, −1, −1, −1, −1). Два таких вектора являются соседними, если их внутреннее произведение равно 8 или, что то же самое, когда их расстояние равно $4{\sqrt {2}}$ .

Альтернативная конструкция основана на 8-вершинном полном графе K ₈ . Вершины графа Госсета можно отождествить с двумя копиями множества ребер K ₈ .Две вершины графа Госсета, происходящие из одной копии, являются смежными, если они соответствуют непересекающимся ребрам графа K ₈ ; две вершины, происходящие из разных копий, являются смежными, если они соответствуют ребрам, имеющим общую вершину. ^[2]

Характеристики

В векторном представлении графа Госсета две вершины находятся на расстоянии два, когда их внутренний продукт равен -8, и на расстоянии три, когда их внутренний продукт равен -24 (что возможно только в том случае, если векторы противоположны друг другу). основанном на ребрах K8 _{В представлении ,} , две вершины графа Госсета находятся на расстоянии три тогда и только тогда, когда они соответствуют разным копиям одного и того же K8 _ребра .Граф Госсета дистанционно регулярен с диаметром три. ^[3]

Индуцированный подграф окрестности любой вершины графа Госсета изоморфен графу Шлефли . ^[3]

Группа автоморфизмов графа Госсета изоморфна группе Кокстера E ₇ и, следовательно, имеет порядок 2903040. Многогранник Госсета 3 ₂₁ является полуправильным многогранником . группа автоморфизмов графа Госсета E ₇ Следовательно , действует транзитивно на его вершинах, что делает его вершинно-транзитивным графом .

Характеристический полином графа Госсета равен ^[4]

(x-27)(x-9)^{7}(x+1)^{27}(x+3)^{21}.\,

Следовательно, этот граф является интегральным графом .

Ссылки

^ Grishukhin, V. P. (2011), "Delone and Voronoĭ polytopes of the root lattice $E 7$ and the dual lattice $E 7 *$ ", Trudy Matematicheskogo Instituta Imeni V. A. Steklova , 275 : 68–86, doi : 10.1134/S0081543811080049 , MR 2962971 , S2CID 120405049 .
^ Хемерс, Виллем Х. (1996), «Дистанция-регулярность и спектр графов» , Линейная алгебра и ее приложения , 236 : 265–278, doi : 10.1016/0024-3795(94)00166-9 , MR 1375618 .
^ Перейти обратно: ^а ^б Kabanov, V. V.; Makhnev, A. A.; Paduchikh, D. V. (2007), "Characterization of some distance-regular graphs by forbidden subgraphs", Doklady Akademii Nauk , 414 (5): 583–586, doi : 10.1134/S1064562407030234 , MR 2451915 , S2CID 119529234 .
^ Брауэр, А.Э.; Рибик, Р.Дж. (1998), «Спектры графов Кокстера», Журнал алгебраической комбинаторики , 8 (1): 15–28, doi : 10.1023/A:1008670825910 , MR 1635551 .

Внешние ссылки

Вайсштейн, Эрик В. «График Госсета» . Математический мир .

[1] Grishukhin, V. P. (2011), "Delone and Voronoĭ polytopes of the root lattice $E 7$ and the dual lattice $E 7 *$ ", Trudy Matematicheskogo Instituta Imeni V. A. Steklova , 275 : 68–86, doi : 10.1134/S0081543811080049 , MR 2962971 , S2CID 120405049 .

[2] Хемерс, Виллем Х. (1996), «Дистанция-регулярность и спектр графов» , Линейная алгебра и ее приложения , 236 : 265–278, doi : 10.1016/0024-3795(94)00166-9 , MR 1375618 .

[kmp-3] Перейти обратно: ^а ^б Kabanov, V. V.; Makhnev, A. A.; Paduchikh, D. V. (2007), "Characterization of some distance-regular graphs by forbidden subgraphs", Doklady Akademii Nauk , 414 (5): 583–586, doi : 10.1134/S1064562407030234 , MR 2451915 , S2CID 119529234 .

[4] Брауэр, А.Э.; Рибик, Р.Дж. (1998), «Спектры графов Кокстера», Журнал алгебраической комбинаторики , 8 (1): 15–28, doi : 10.1023/A:1008670825910 , MR 1635551 .

[1]

[2]

[3]

[4]