Контроллер артикуляции модели мозжечка

( Арифметический компьютер модели мозжечка CMAC ) представляет собой тип нейронной сети, основанной на модели мозжечка млекопитающих . Он также известен как контроллер артикуляции модели мозжечка. Это разновидность ассоциативной памяти . [2]
CMAC был впервые предложен Джеймсом Альбусом в 1975 году в качестве средства моделирования функций для контроллеров роботов. [1] (отсюда и название), но широко использовался в обучении с подкреплением , а также для автоматической классификации в сообществе машинного обучения . CMAC является расширением модели перцептрона . Он вычисляет функцию для входные размеры. Пространство ввода разделено на гиперпрямоугольники, каждый из которых связан с ячейкой памяти. Содержимое ячеек памяти — это веса, которые корректируются во время обучения. Обычно используется более одного квантования входного пространства, так что любая точка входного пространства связана с несколькими гиперпрямоугольниками и, следовательно, с несколькими ячейками памяти. Выходные данные CMAC представляют собой алгебраическую сумму весов во всех ячейках памяти, активированных входной точкой.
Изменение значения входной точки приводит к изменению набора активированных гиперпрямоугольников и, следовательно, к изменению набора ячеек памяти, участвующих в выходе CMAC. Таким образом, выходные данные CMAC сохраняются распределенным образом, так что выходные данные, соответствующие любой точке входного пространства, получаются из значения, хранящегося в нескольких ячейках памяти (отсюда и название ассоциативная память). Это обеспечивает обобщение.
Строительные блоки
[ редактировать ]
На соседнем изображении есть два входа в CMAC, представленные в виде 2D-пространства. Для разделения этого пространства двумя перекрывающимися сетками (одна показана более жирными линиями) использовались две функции квантования. Один вход показан ближе к середине, и это активирует две ячейки памяти, соответствующие заштрихованной области. Если рядом с показанной окажется другая точка, она будет использовать некоторые из тех же ячеек памяти, что обеспечит обобщение.
CMAC обучается путем представления пар входных точек и выходных значений и корректировки весов в активированных ячейках на долю ошибки, наблюдаемой на выходе. Этот простой алгоритм обучения имеет доказательство сходимости. [3]
Добавление функции ядра к гиперпрямоугольнику является нормальным явлением, так что точки, падающие к краю гиперпрямоугольника, активируются меньше, чем точки, падающие ближе к центру. [4]
Одной из основных проблем, возникающих при практическом использовании CMAC, является требуемый объем памяти, который напрямую связан с количеством используемых ячеек. Обычно это решается использованием хеш-функции и предоставлением памяти только для реальных ячеек, которые активируются входными данными.
Одношаговый конвергентный алгоритм
[ редактировать ]Первоначально для обновления весов CMAC используется метод наименьших среднеквадратических значений (LMS). Конвергенция использования LMS для обучения CMAC чувствительна к скорости обучения и может привести к расхождению. В 2004 году [5] для онлайн-обучения CMAC был введен рекурсивный алгоритм наименьших квадратов (RLS). Нет необходимости настраивать скорость обучения. Его сходимость доказана теоретически и может быть гарантированно сходится за один шаг. Вычислительная сложность этого алгоритма RLS составляет O(N3).
Инфраструктура аппаратной реализации
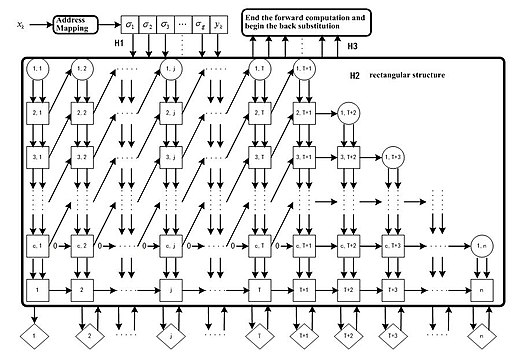
[ редактировать ]На основе QR-разложения алгоритм (QRLS) был дополнительно упрощен и теперь имеет сложность O (N). Следовательно, это значительно снижает использование памяти и затраты времени. Была представлена структура параллельного конвейерного массива для реализации этого алгоритма. [6]
В целом, используя алгоритм QRLS, можно гарантировать сходимость нейронной сети CMAC, а веса узлов можно обновлять за один этап обучения. Его структура параллельного конвейерного массива предлагает большой потенциал для реализации в аппаратном обеспечении для крупномасштабного промышленного использования.
Непрерывный CMAC
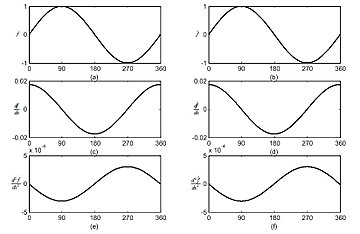
[ редактировать ]Поскольку прямоугольная форма функций рецептивного поля CMAC обеспечивает прерывистую аппроксимацию лестничной функции, путем интеграции CMAC с функциями B-сплайнов непрерывный CMAC предлагает возможность получения производных любого порядка аппроксимированных функций.
Глубокий CMAC
[ редактировать ]В последние годы многочисленные исследования подтвердили, что объединение нескольких неглубоких структур в одну глубокую структуру позволяет всей системе обеспечить лучшее представление данных и, таким образом, более эффективно решать нелинейные и сложные задачи. В 2018 году [7] была предложена структура глубокого CMAC (DCMAC) и разработан алгоритм обратного распространения ошибки для оценки параметров DCMAC. Экспериментальные результаты задачи адаптивного шумоподавления показали, что предлагаемый DCMAC может обеспечить лучшую производительность шумоподавления по сравнению с обычным однослойным CMAC.
Краткое содержание
[ редактировать ]| Масштабируемость | Просто распространить на миллионы нейронов или дальше. |
| Конвергенция | Обучение всегда может сводиться в один этап |
| Производные функции | Легко получить, используя интерполяцию B-сплайнами. |
| Аппаратная структура | Параллельная структура трубопровода |
| Использование памяти | Линейный по количеству нейронов |
| Вычислительная сложность | НА) |
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Перейти обратно: а б Альбус, Дж.С. (1 сентября 1975 г.). «Новый подход к управлению манипулятором: контроллер артикуляции модели мозжечка (CMAC)» . Журнал динамических систем, измерений и управления . 97 (3): 220–227. дои : 10.1115/1.3426922 . ISSN 0022-0434 .
- ^ Альбус, Джеймс С. (август 1979 г.). «Механизмы планирования и решения проблем в мозге» . Математические биологические науки . 45 (3–4): 247–293. дои : 10.1016/0025-5564(79)90063-4 .
- ^ Вонг, Ю.; Сидерис, А. (январь 1992 г.). «Обучение конвергенции в контроллере артикуляции модели мозжечка» . Транзакции IEEE в нейронных сетях . 3 (1): 115–121. дои : 10.1109/72.105424 .
- ^ PCE An, WT Miller и PC Parks, Улучшения конструкции ассоциативной памяти для контроллеров артикуляции модели мозжечка, Proc. ICANN, стр. 1207–10, 1991 г.
- ^ Цинь, Тин; Чен, Цзунхай; Чжан, Хайтао; Ли, Сифу; Сян, Вэй; Ли, Мин (1 февраля 2004 г.). «Алгоритм обучения CMAC на основе RLS» . Нейронная обработка писем . 19 (1): 49–61. дои : 10.1023/B:NEPL.0000016847.18175.60 . ISSN 1573-773X .
- ^ Перейти обратно: а б Цинь, Тин; Чжан, Хайтао; Чен, Цзунхай; Сян, Вэй (1 августа 2005 г.). «Непрерывный CMAC-QRLS и его систолический массив» . Нейронная обработка писем . 22 (1): 1–16. дои : 10.1007/s11063-004-2694-0 . ISSN 1573-773X .
- ^ Ца, Ю; Чу, Хао-Чун; Фанг, Ши-Хау; Ли, Юнгси; Лин, Чи-Мин (2018). «Адаптивное шумоподавление с использованием контроллера артикуляции глубокой модели мозжечка» . Доступ IEEE . 6 : 37395–37402. дои : 10.1109/ACCESS.2018.2827699 . ISSN 2169-3536 .
Дальнейшее чтение
[ редактировать ]- Альбус, Дж. С. (1971). « Теория функции мозжечка ». В: Математические биологические науки , том 10, номера 1/2, февраль 1971 г., стр. 25–61
- Альбус, Дж. С. (1975). « Новый подход к управлению манипулятором: контроллер артикуляции модели мозжечка (CMAC) ». В: Труды журнала ASME по динамическим системам, измерениям и контролю , сентябрь 1975 г., стр. 220 – 227
- Альбус, Дж. С. (1979). « Механизмы планирования и решения проблем в мозгу ». В: Mathematical Biosciences 45, стр. 247–293, 1979.
- Иван Л. и Стенгель Р. « Применение нейронных сетей в топливных процессорах для топливных элементов » в IEEE Transactions on Vehicle Technology , Vol. 50 (1), стр. 125–143, 2001.
- Цао, Ю. (2018). « Адаптивное шумоподавление с использованием контроллера артикуляции глубокой модели мозжечка ». В: IEEE Access, 6, апрель 2018 г., стр. 37395-37402.
Внешние ссылки
[ редактировать ]- контроллере артикуляции модели мозжечка (CMAC) Блог Тин Цинь о . Подробнее об одношаговом конвергентном алгоритме, разработке кода и т. д.
