Искаженная схема

Искаженная схема — это криптографический протокол , который обеспечивает двусторонние безопасные вычисления , в которых две недоверчивые стороны могут совместно оценивать функцию на основе своих частных входных данных без присутствия доверенной третьей стороны. В протоколе искаженной схемы функция должна быть описана как булева схема .

История искаженных цепей сложна. Изобретение искаженной схемы было приписано Эндрю Яо , поскольку Яо представил эту идею во время устной презентации статьи. в ФОКС '86. Это было задокументировано Одедом Гольдрейхом в 2003 году. Первый письменный документ об этой технике был написан Голдрейхом, Микали и Вигдерсон в STOC '87. Термин «искаженная схема» впервые был использован Бивером, Микали и Рогавеем в STOC'90. Протокол Яо, решающий «Проблему миллионеров Яо», был первым примером безопасных вычислений, однако он не имеет прямого отношения к искаженным схемам.

Предыстория

Незаметный трансфер

В протоколе искаженной цепи мы используем не обращающую внимания передачу . При забывчивой передаче строка передается между отправителем и получателем следующим образом: отправитель имеет две строки. $S_{0}$ и $S_{1}$. Получатель выбирает $b\in \{0,1\}$ и отправитель отправляет $S_{b}$ с забывчивым протоколом передачи, таким, что

1. получатель не получает никакой информации о неотправленной строке $S_{(1-b)}$,
2. ценность $b$ не раскрывается отправителю.

Обратите внимание, что хотя получатель не знает $S_{0},S_{1}$ значений, на практике получатель знает некоторую информацию о том, что $S_{b}$ кодирует так, чтобы получатель не делал слепой выбор $b$. То есть, если $S_{0}$ кодирует ложное значение, $S_{1}$ кодирует истинное значение, и получатель хочет получить закодированное истинное значение, получатель выбирает $b=1$.

Незаметную передачу можно реализовать с использованием асимметричной криптографии, такой как криптосистема RSA .

Определения и обозначения

Оператор $\parallel$ строк это конкатенация . Оператор $\oplus$ это побитовое XOR . k — параметр безопасности и длина ключей. Оно должно быть больше 80 и обычно устанавливается на уровне 128.

Протокол искаженной цепи

Протокол состоит из 6 шагов следующим образом:

1. Основная функция (например, в задаче миллионеров функция сравнения) описывается как булева схема с двумя входными вентилями. Схема известна обеим сторонам. Этот шаг может быть выполнен заранее третьей стороной.
2. Алиса искажает (шифрует) схему. Мы называем Алису обманщицей .
3. Алиса отправляет искаженную схему вместе со своими зашифрованными входными данными. Бобу
4. Чтобы рассчитать схему, Бобу также необходимо исказить свои собственные входные данные. Для этого ему нужна помощь Алисы, ведь только шифровальщик умеет шифровать. Наконец, Боб может зашифровать вводимые данные посредством неконтролируемой передачи. Согласно определению, данному выше, Боб является получателем, а Алиса — отправителем при этой не обращающей внимания передаче.
5. Боб оценивает (расшифровывает) схему и получает зашифрованные выходные данные. Мы называем Боба оценщиком .
6. Алиса и Боб общаются, чтобы узнать результат.

Генерация схемы

Булеву схему для небольших функций можно сгенерировать вручную. Обычно схему составляют из двухвходовых «исключающее ИЛИ» и «И» логических элементов . Важно, чтобы сгенерированная схема имела минимальное количество вентилей И (см. Свободная оптимизация XOR ). Существуют методы, которые генерируют оптимизированную схему с точки зрения количества логических элементов И, используя логического синтеза . технику Схема «Задачи миллионеров» представляет собой схему цифрового компаратора (которая представляет собой цепочку полных сумматоров, работающих как вычитатель и выдающих флаг переноса ). Схема полного сумматора может быть реализована с использованием только одного вентиля И и нескольких вентилей исключающее ИЛИ . Это означает, что общее количество логических элементов И для схемы «Задачи миллионеров» равно разрядности входов.

Garbling

Провода и их метки на вентиле И

Построение таблицы истинности вентиля И.

На этом этапе Алиса (искажитель) шифрует логическую схему , чтобы получить искаженную схему . Алиса назначает две случайно сгенерированные строки, называемые метками, каждому проводу в схеме: одну для логической семантики 0 и одну для 1. (Метка имеет длину k бит, где k — параметр безопасности и обычно имеет значение 128.) Далее она идет ко всем элементам схемы и заменяет 0 и 1 в таблицах истинности соответствующими метками. В таблице ниже показана таблица истинности для логического элемента И с двумя входами. $w^{a},w^{b}$ и вывод $w^{c}$:

а	б	с
0	0	0
0	1	0
1	0	0
1	1	1

Алиса заменила 0 и 1 соответствующими метками:

а	б	с
$X_{0}^{a}$	$X_{0}^{b}$	$X_{0}^{c}$
$X_{0}^{a}$	$X_{1}^{b}$	$X_{0}^{c}$
$X_{1}^{a}$	$X_{0}^{b}$	$X_{0}^{c}$
$X_{1}^{a}$	$X_{1}^{b}$	$X_{1}^{c}$

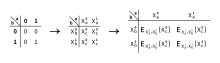
Затем она шифрует выходную запись таблицы истинности соответствующими двумя входными метками. Зашифрованная таблица называется искаженной таблицей. Это сделано для того, чтобы расшифровать искаженную таблицу можно было только в том случае, если у него есть две правильные входные метки. В таблице ниже, $Enc_{k}(X)$ с двойным ключом — это симметричное шифрование , в котором k — секретный ключ, а X — значение, подлежащее шифрованию (см. Блочный шифр с фиксированным ключом ).

Искаженный стол
$Enc_{X_{0}^{a},X_{0}^{b}}(X_{0}^{c})$
$Enc_{X_{0}^{a},X_{1}^{b}}(X_{0}^{c})$
$Enc_{X_{1}^{a},X_{0}^{b}}(X_{0}^{c})$
$Enc_{X_{1}^{a},X_{1}^{b}}(X_{1}^{c})$

После этого Алиса случайным образом переставляет таблицу так, что выходное значение невозможно определить по строке. имя протокола Искаженное получено из этой случайной перестановки.

Передача данных

Алиса отправляет Бобу вычисленные искаженные таблицы для всех элементов схемы. Бобу нужны метки ввода, чтобы открыть искаженные таблицы. Таким образом, Алиса выбирает метки, соответствующие ее входным данным. $a$ и отправляет их Бобу. Например, если ввод Алисы $\mathbf {a} =a_{4}a_{3}a_{2}a_{1}a_{0}=01101$, затем она отправляет $X_{0}^{a_{4}}$, $X_{1}^{a_{3}}$, $X_{1}^{a_{2}}$, $X_{0}^{a_{1}}$, и $X_{1}^{a_{0}}$ Бобу. Боб ничего не узнает о вкладе Алисы. $\mathbf {a}$, поскольку метки генерируются Алисой случайным образом и для Боба они выглядят как случайные строки.

Бобу также нужны метки, соответствующие его входным данным. Он получает свои ярлыки путем не обращая внимания на передачу каждого бита своего ввода. Например, если входные данные Боба $\mathbf {b} =b_{4}b_{3}b_{2}b_{1}b_{0}=10100$, Боб сначала спрашивает $b_{0}=0$ между ярлыками Алисы $X_{0}^{b_{0}}$ и $X_{1}^{b_{0}}$. 1 из 2 Через невнимательную передачу он получает $X_{0}^{b_{0}}$ и так далее. После забывчивых передач Алиса ничего не узнает о вводе Боба, а Боб ничего не узнает о других метках.

Оценка

После передачи данных у Боба остаются искаженные таблицы и метки входных данных. Он проходит через все ворота один за другим и пытается расшифровать строки в их искаженных таблицах. Он может открыть одну строку для каждой таблицы и получить соответствующую выходную метку: $X^{c}=Dec_{X^{a},X^{b}}(garbled\_table[i])$, где $0\leq i\leq 3$. Он продолжает оценку, пока не достигнет выходных меток.

Выявление результатов

После оценки Боб получает выходную метку: $X^{c}$, и Алиса знает его сопоставление с логическим значением, поскольку у нее есть обе метки: $X_{0}^{c}$ и $X_{1}^{c}$. Либо Алиса может поделиться своей информацией с Бобом, либо Боб может раскрыть выходные данные Алисе, так что один или оба из них изучат выходные данные.

Оптимизация

Точка и перестановка

В этой оптимизации Алиса генерирует случайный бит, $s$, называется битом выбора для каждого провода $w$. Она устанавливает первый бит метки 0, $X_{0}^{a}$ к $s$ и первый бит метки 1, $X_{1}^{a}$, к ${\bar {s}}$ ( НЕ из $s$). Она делает то же самое с проволокой $w^{b}$. Затем она, вместо случайных перестановок, сортирует искаженную таблицу в соответствии с входными битами выбора. Таким образом, Бобу не нужно проверять все четыре строки таблицы, чтобы найти правильную, поскольку он получает биты указателя с каждой меткой провода и может найти правильную строку и расшифровать ее за одну попытку. Это снижает нагрузку на оценку в 4 раза. Он также ничего не раскрывает о выходном значении, поскольку биты выбора генерируются случайным образом.

Сокращение строк

Эта оптимизация уменьшает размер искаженных таблиц с 4 до 3 строк. Здесь вместо случайной генерации метки для выходного провода вентиля Алиса генерирует ее, используя функцию входных меток. Она генерирует выходные метки так, что первая запись в искаженной таблице становится нулевой и ее больше не нужно отправлять:

${\begin{aligned}&Enc_{X_{0}^{a},X_{0}^{b}}(X_{0}^{c})=0\\&X_{0}^{c}=Dec_{X_{0}^{a},X_{0}^{b}}(0).\end{aligned}}$

Бесплатный XOR

В этой оптимизации Алиса генерирует глобальное случайное (k-1)-битное значение. $R$ который держится в секрете. Во время искажения входных ворот $w^{a}$ и $w^{b}$, она только генерирует метки $(X_{0}^{a},X_{0}^{b})$ и вычисляет другие метки как $X_{1}^{a}=X_{0}^{a}\oplus (R\parallel 1)$ и $X_{1}^{b}=X_{0}^{b}\oplus (R\parallel 1)$. Используя эти значения, метка выходного провода элемента XOR $w^{c}$ с входными проводами $w^{a}$, $w^{b}$ установлено на $X^{c}=X^{a}\oplus X^{b}$. Доказательство безопасности случайной модели Oracle для этой оптимизации приведено в статье Free-XOR.

Значение

Свободная оптимизация XOR подразумевает важный момент: объем передачи данных (коммуникации), а также количество операций шифрования и дешифрования (вычислений) протокола искаженной схемы зависит только от количества логических элементов И в логической схеме, а не от логических элементов исключающего ИЛИ . Таким образом, между двумя логическими схемами, представляющими одну и ту же функцию, предпочтительна схема с меньшим количеством логических элементов И.

Блок-шифр с фиксированным ключом

Этот метод позволяет эффективно искажать и оценивать логические элементы AND с использованием AES с фиксированным ключом вместо дорогостоящей криптографической хэш-функции , такой как SHA-2 . В этой схеме искажения, совместимой с методами Free XOR и Row Reduction , выходной ключ $X^{c}$ шифруется входным токеном $X^{a}$ и $X^{b}$ используя функцию шифрования $Enc(X^{a},X^{b},T,X^{c})=\pi (K)\oplus K\oplus X^{c}$, где $K=2X^{a}\oplus 4X^{b}\oplus T$, $\pi$ представляет собой блочный шифр с фиксированным ключом (например, созданный с помощью AES ), и $T$ это уникальный номер для каждого шлюза (например, идентификатор шлюза), называемый tweak .

Половина И

Эта оптимизация уменьшает размер искаженной таблицы для логических элементов AND с 3 строк при сокращении строк до 2 строк. Показано, что это теоретический минимум числа строк в искаженной таблице для определенного класса методов искажения.

Безопасность

Искаженный контур Яо защищен от получестного противника. Злоумышленники этого типа следуют протоколу и не совершают никаких злонамеренных действий, но пытаются нарушить конфиденциальность ввода другой стороны, тщательно проверяя сообщения, передаваемые по протоколу.

Гораздо сложнее обеспечить защиту этого протокола от злонамеренного противника, который отклоняется от протокола. Одним из первых решений, позволяющих защитить протокол от злоумышленников, является использование доказательства с нулевым разглашением для предотвращения вредоносных действий во время протокола. В течение многих лет этот подход рассматривался скорее как теоретическое решение, чем практическое решение, из-за его сложности. Но показано, что его можно использовать с небольшими накладными расходами. Другой подход заключается в использовании нескольких сборщиков мусора для схемы и проверке правильности подмножества из них, а затем использовании остальных для вычислений в надежде, что, если искажитель был злонамеренным, он будет обнаружен на этапе проверки. Другое решение состоит в том, чтобы сделать схему искажения аутентифицированной, чтобы оценщик мог проверить искаженную схему.

См. также

• Криптография
• ЮАР
• Безопасные многосторонние вычисления
• Проблема миллионеров Яо

Дальнейшее чтение

• «Искаженная схема Яо» (PDF) . CS598 . Иллинойс.edu . Проверено 18 октября 2016 г.