Обобщенная логистическая функция

Влияние изменения параметра A. Все остальные параметры равны 1.

Влияние изменения параметра B. A = 0, все остальные параметры равны 1.

Влияние изменения параметра C. A = 0, все остальные параметры равны 1.

Влияние изменения параметра K. A = 0, все остальные параметры равны 1.

Влияние изменения параметра Q. A = 0, все остальные параметры равны 1.

Эффект изменения параметра $\nu$ . А = 0, все остальные параметры равны 1.

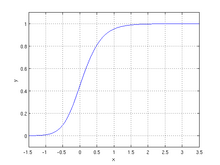
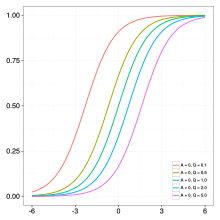
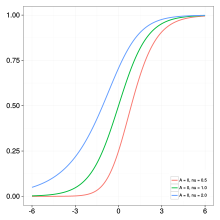
Обобщенная логистическая функция или кривая является расширением логистической или сигмовидной функции. Первоначально разработанный для моделирования роста, он позволяет создавать более гибкие S-образные кривые. Функцию иногда называют кривой Ричардса в честь Ф. Дж. Ричардса , который предложил общую форму семейства моделей в 1959 году.

Определение

Кривая Ричардса имеет следующий вид:

Y(t)=A+{K-A \over (C+Qe^{-Bt})^{1/\nu }}

где $Y$ = вес, рост, размер и т. д., и $t$ = время. Он имеет шесть параметров:

$A$ : левая горизонтальная асимптота;
$K$ : правая горизонтальная асимптота, когда $C=1$ . Если $A=0$ и $C=1$ затем $K$ называется пропускной способностью ;
$B$ : темп роста;
$\nu >0$ : влияет на то, вблизи какой асимптоты происходит максимальный рост.
$Q$ : связано со значением $Y(0)$
$C$ : обычно принимает значение 1. В противном случае верхняя асимптота равна $A+{K-A \over C^{\,1/\nu }}$

Уравнение также можно записать:

Y(t)=A+{K-A \over (C+e^{-B(t-M)})^{1/\nu }}

где $M$ можно рассматривать как начальный момент, когда $Y(M)=A+{K-A \over (C+1)^{1/\nu }}$ . Включая оба $Q$ и $M$ может быть удобно:

Y(t)=A+{K-A \over (C+Qe^{-B(t-M)})^{1/\nu }}

это представление упрощает настройку как времени начала, так и значения $Y$ в это время.

Логистическая функция с максимальным темпом роста во времени $M$ , это тот случай, когда $Q=\nu =1$ .

Обобщенное логистическое дифференциальное уравнение

Частным случаем обобщенной логистической функции является:

Y(t)={K \over (1+Qe^{-\alpha \nu (t-t_{0})})^{1/\nu }}

что является решением дифференциального уравнения Ричардса (ДДУ):

Y^{\prime }(t)=\alpha \left(1-\left({\frac {Y}{K}}\right)^{\nu }\right)Y

с начальным состоянием

Y(t_{0})=Y_{0}

где

Q=-1+\left({\frac {K}{Y_{0}}}\right)^{\nu }

при условии, что $\nu >0$ и $\alpha >0$

Классическое логистическое дифференциальное уравнение является частным случаем приведенного выше уравнения, при этом $\nu =1$ , тогда как кривая Гомпертца восстанавливается в пределе $\nu \rightarrow 0^{+}$ при условии, что:

\alpha =O\left({\frac {1}{\nu }}\right)

Фактически, для небольших $\nu$ это

Y^{\prime }(t)=Yr{\frac {1-\exp \left(\nu \ln \left({\frac {Y}{K}}\right)\right)}{\nu }}\approx rY\ln \left({\frac {Y}{K}}\right)

RDE моделирует многие явления роста, возникающие в таких областях, как онкология и эпидемиология.

Градиент обобщенной логистической функции

При оценке параметров на основе данных часто необходимо вычислить частные производные логистической функции по параметрам в данной точке данных. $t$ (видеть ^[1]). Для случая, когда $C=1$ ,

{\begin{aligned}\\{\frac {\partial Y}{\partial A}}&=1-(1+Qe^{-B(t-M)})^{-1/\nu }\\\\{\frac {\partial Y}{\partial K}}&=(1+Qe^{-B(t-M)})^{-1/\nu }\\\\{\frac {\partial Y}{\partial B}}&={\frac {(K-A)(t-M)Qe^{-B(t-M)}}{\nu (1+Qe^{-B(t-M)})^{{\frac {1}{\nu }}+1}}}\\\\{\frac {\partial Y}{\partial \nu }}&={\frac {(K-A)\ln(1+Qe^{-B(t-M)})}{\nu ^{2}(1+Qe^{-B(t-M)})^{\frac {1}{\nu }}}}\\\\{\frac {\partial Y}{\partial Q}}&=-{\frac {(K-A)e^{-B(t-M)}}{\nu (1+Qe^{-B(t-M)})^{{\frac {1}{\nu }}+1}}}\\\\{\frac {\partial Y}{\partial M}}&=-{\frac {(K-A)QBe^{-B(t-M)}}{\nu (1+Qe^{-B(t-M)})^{{\frac {1}{\nu }}+1}}}\\\end{aligned}}

Особые случаи

Следующие функции являются частными случаями кривых Ричардса:

Сноски

^ Фекедулен, Деста; Майритин П. Мак Сиуртен; Джим Дж. Колберт (1999). «Оценка параметров нелинейных моделей роста в лесном хозяйстве» (PDF) . Сильва Фенника . 33 (4): 327–336. дои : 10.14214/sf.653 . Архивировано из оригинала (PDF) 29 сентября 2011 г. Проверено 31 мая 2011 г.

Ссылки

Ричардс, Ф.Дж. (1959). «Гибкая функция роста для эмпирического использования». Журнал экспериментальной ботаники . 10 (2): 290–300. дои : 10.1093/jxb/10.2.290 .
Пелла, Дж.С.; Томлинсон, ПК (1969). «Обобщенная модель серийного производства». Бык. Интер-Ам. Троп. Тунец Комм . 13 : 421–496.
Лей, ЮК; Чжан, С.Ю. (2004). «Особенности и частные производные модели роста Берталанфи – Ричардса в лесном хозяйстве». Нелинейный анализ: моделирование и управление . 9 (1): 65–73. дои : 10.15388/NA.2004.9.1.15171 .

[fekedulegn1999parameter-1] Фекедулен, Деста; Майритин П. Мак Сиуртен; Джим Дж. Колберт (1999). «Оценка параметров нелинейных моделей роста в лесном хозяйстве» (PDF) . Сильва Фенника . 33 (4): 327–336. дои : 10.14214/sf.653 . Архивировано из оригинала (PDF) 29 сентября 2011 г. Проверено 31 мая 2011 г.

[1]