Монотонная кубическая интерполяция

В математической области анализа численного монотонная кубическая интерполяция — это вариант кубической интерполяции , который сохраняет монотонность набора данных интерполируемого .

Монотонность сохраняется при линейной интерполяции , но не гарантируется кубической интерполяцией .

Монотонная кубическая интерполяция Эрмита

Пример, показывающий немонотонную кубическую интерполяцию (красным цветом) и монотонную кубическую интерполяцию (синим цветом) монотонного набора данных.

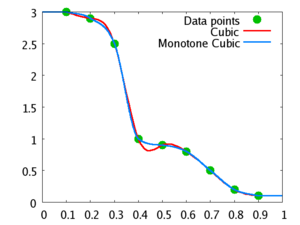
Монотонную интерполяцию можно выполнить с помощью кубического сплайна Эрмита с касательными. $m_{i}$ модифицирован для обеспечения монотонности полученного сплайна Эрмита.

Также доступен алгоритм монотонной пятерной интерполяции Эрмита.

Интерполянтный выбор

Существует несколько способов выбора интерполирующих касательных для каждой точки данных. В этом разделе будет описано использование метода Фрича – Карлсона. Обратите внимание, что требуется только один проход алгоритма.

Пусть точки данных будут $(x_{k},y_{k})$ индексируется в отсортированном порядке для $k=1,\,\dots \,n$.

1. Вычислите наклоны секущих между последовательными точками:

   $\delta _{k}={\frac {y_{k+1}-y_{k}}{x_{k+1}-x_{k}}}$

   для $k=1,\,\dots \,n-1$.
   
   
2. Эти назначения являются предварительными и могут быть заменены на оставшихся этапах. Инициализируйте касательные в каждой внутренней точке данных как среднее значение секущих,

   $m_{k}={\frac {\delta _{k-1}+\delta _{k}}{2}}$

   для $k=2,\,\dots \,n-1$.
   
   Для конечных точек используйте односторонние разности:

   $m_{1}=\delta _{1}\quad {\text{ and }}\quad m_{n}=\delta _{n-1}\,$.

   Если $\delta _{k-1}$ и $\delta _{k}$ имеют противоположные знаки, множество $m_{k}=0$.
   
   
3. Для $k=1,\,\dots \,n-1$, где бы то ни было $\delta _{k}=0$ (где когда-либо два последовательных $y_{k}=y_{k+1}$ равны),
   набор $m_{k}=m_{k+1}=0,$ поскольку сплайн, соединяющий эти точки, должен быть плоским, чтобы сохранить монотонность.
   Игнорируйте шаги 4 и 5 для тех, $k\,$.
   
   
4. Позволять

   $\alpha _{k}=m_{k}/\delta _{k}\quad {\text{ and }}\quad \beta _{k}=m_{k+1}/\delta _{k}$.

   Если либо $\alpha _{k}$ или $\beta _{k}$ отрицательно, то точки входных данных не являются строго монотонными и $(x_{k},\,y_{k})$ является локальным экстремумом. В таких случаях кусочно -монотонные кривые все же можно получить, выбрав $m_{k}=0\,$ если $\alpha _{k}<0$ или $m_{k+1}=0\,$ если $\beta _{k}<0$, хотя строгая монотонность в глобальном масштабе невозможна.
   
   
5. Чтобы предотвратить перерегулирование и обеспечить монотонность, должно быть выполнено хотя бы одно из следующих трех условий:

(а) функция

$\phi _{k}=\alpha _{k}-{\frac {(2\alpha _{k}+\beta _{k}-3)^{2}}{3(\alpha _{k}+\beta _{k}-2)}}>0\,$, или

(б) $\alpha _{k}+2\beta _{k}-3\leq 0\,$, или

(с) $2\alpha _{k}+\beta _{k}-3\leq 0\,$.

Только условия (а) достаточно для обеспечения строгой монотонности: $\phi _{k}$ должен быть положительным.

Один простой способ удовлетворить это ограничение — ограничить вектор $(\alpha _{k},\,\beta _{k})$ к окружности радиуса 3. То есть, если $\alpha _{k}^{2}+\beta _{k}^{2}>9\,$, затем установите

$\tau _{k}={\frac {3}{\sqrt {\alpha _{k}^{2}+\beta _{k}^{2}}}}\,$,

и измените масштаб касательных через

$m_{k}=\tau _{k}\,\alpha _{k}\,\delta _{k}\quad {\text{ and }}\quad m_{k+1}=\tau _{k}\,\beta _{k}\,\delta _{k}\,$.

В качестве альтернативы достаточно ограничить $\alpha _{k}\leq 3$ и $\beta _{k}\leq 3\,$. Для этого, если $\alpha _{k}>3\,$, затем установите $m_{k}=3\,\delta _{k}\,$, и если $\beta _{k}>3\,$, затем установите $m_{k+1}=3\,\delta _{k}\,$.

Кубическая интерполяция

После предварительной обработки, описанной выше, оценка интерполированного сплайна эквивалентна кубическому сплайну Эрмита с использованием данных $x_{k}$, $y_{k}$, и $m_{k}$ для $k=1,\,\dots \,n$.

Чтобы оценить на $x$, найдите индекс $k$ в той последовательности, где $x$, лежит между $x_{k}$, и $x_{k+1}$, то есть: $x_{k}\leq x\leq x_{k+1}$. Рассчитать

$\Delta =x_{k+1}-x_{k}\quad {\text{ and }}\quad t={\frac {x-x_{k}}{\Delta }}$

тогда интерполированное значение равно

$f_{\text{interpolated}}(x)=y_{k}\cdot h_{00}(t)+\Delta \cdot m_{k}\cdot h_{10}(t)+y_{k+1}\cdot h_{01}(t)+\Delta \cdot m_{k+1}\cdot h_{11}(t)$

где $h_{ii}$ являются базисными функциями кубического сплайна Эрмита .

Пример реализации

Следующая реализация JavaScript принимает набор данных и создает монотонную интерполянтную функцию кубического сплайна:

/*
 * Monotone cubic spline interpolation
 * Usage example listed at bottom; this is a fully-functional package. For
 * example, this can be executed either at sites like
 * https://www.programiz.com/javascript/online-compiler/
 * or using nodeJS.
 */
function DEBUG(s) {
    /* Uncomment the following to enable verbose output of the solver: */
    //console.log(s);
}
var j = 0;
var createInterpolant = function(xs, ys) {
    var i, length = xs.length;
    
    // Deal with length issues
    if (length != ys.length) { throw 'Need an equal count of xs and ys.'; }
    if (length === 0) { return function(x) { return 0; }; }
    if (length === 1) {
        // Impl: Precomputing the result prevents problems if ys is mutated later and allows garbage collection of ys
        // Impl: Unary plus properly converts values to numbers
        var result = +ys[0];
        return function(x) { return result; };
    }
    
    // Rearrange xs and ys so that xs is sorted
    var indexes = [];
    for (i = 0; i < length; i++) { indexes.push(i); }
    indexes.sort(function(a, b) { return xs[a] < xs[b] ? -1 : 1; });
    var oldXs = xs, oldYs = ys;
    // Impl: Creating new arrays also prevents problems if the input arrays are mutated later
    xs = []; ys = [];
    // Impl: Unary plus properly converts values to numbers
    for (i = 0; i < length; i++) { xs.push(+oldXs[indexes[i]]); ys.push(+oldYs[indexes[i]]); }

    DEBUG("debug: xs = [ " + xs + " ]")
    DEBUG("debug: ys = [ " + ys + " ]")
    
    // Get consecutive differences and slopes
    var dys = [], dxs = [], ms = [];
    for (i = 0; i < length - 1; i++) {
        var dx = xs[i + 1] - xs[i], dy = ys[i + 1] - ys[i];
        dxs.push(dx); dys.push(dy); ms.push(dy/dx);
    }
    // Get degree-1 coefficients
    var c1s = [ms[0]];
    for (i = 0; i < dxs.length - 1; i++) {
        var m = ms[i], mNext = ms[i + 1];
        if (m*mNext <= 0) {
            c1s.push(0);
        } else {
            var dx_ = dxs[i], dxNext = dxs[i + 1], common = dx_ + dxNext;
            c1s.push(3*common/((common + dxNext)/m + (common + dx_)/mNext));
        }
    }
    c1s.push(ms[ms.length - 1]);

    DEBUG("debug: dxs = [ " + dxs + " ]")
    DEBUG("debug: ms = [ " + ms + " ]")
    DEBUG("debug: c1s.length = " + c1s.length)
    DEBUG("debug: c1s = [ " + c1s + " ]")
    
    // Get degree-2 and degree-3 coefficients
    var c2s = [], c3s = [];
    for (i = 0; i < c1s.length - 1; i++) {
        var c1 = c1s[i];
        var m_ = ms[i];
        var invDx = 1/dxs[i];
        var common_ = c1 + c1s[i + 1] - m_ - m_;
        DEBUG("debug: " + i + ". c1 = " + c1);
        DEBUG("debug: " + i + ". m_ = " + m_);
        DEBUG("debug: " + i + ". invDx = " + invDx);
        DEBUG("debug: " + i + ". common_ = " + common_);
        c2s.push((m_ - c1 - common_)*invDx);
        c3s.push(common_*invDx*invDx);
    }
    DEBUG("debug: c2s = [ " + c2s + " ]")
    DEBUG("debug: c3s = [ " + c3s + " ]")

    // Return interpolant function
    return function(x) {
        // The rightmost point in the dataset should give an exact result
        var i = xs.length - 1;
        //if (x == xs[i]) { return ys[i]; }
        
        // Search for the interval x is in, returning the corresponding y if x is one of the original xs
        var low = 0, mid, high = c3s.length - 1, rval, dval;
        while (low <= high) {
            mid = Math.floor(0.5*(low + high));
            var xHere = xs[mid];
            if (xHere < x) { low = mid + 1; }
            else if (xHere > x) { high = mid - 1; }
            else {
                j++;
                i = mid;
                var diff = x - xs[i];
                rval = ys[i] + diff * (c1s[i] + diff *  (c2s[i] + diff * c3s[i]));
                dval = c1s[i] + diff * (2*c2s[i] + diff * 3*c3s[i]);
                DEBUG("debug: " + j + ". x = " + x + ". i = " + i + ", diff = " + diff + ", rval = " + rval + ", dval = " + dval);
                return [ rval, dval ];
            }
        }
        i = Math.max(0, high);

        // Interpolate
        var diff = x - xs[i];
        j++;
        rval = ys[i] + diff * (c1s[i] + diff *  (c2s[i] + diff * c3s[i]));
        dval = c1s[i] + diff * (2*c2s[i] + diff * 3*c3s[i]);
        DEBUG("debug: " + j + ". x = " + x + ". i = " + i + ", diff = " + diff + ", rval = " + rval + ", dval = " + dval);
        return [ rval, dval ];
    };
};

/*
   Usage example below will approximate x^2 for 0 <= x <= 4.

   Command line usage example (requires installation of nodejs):
   node monotone-cubic-spline.js
*/

var X = [0, 1, 2, 3, 4];
var F = [0, 1, 4, 9, 16];
var f = createInterpolant(X,F);
var N = X.length;
console.log("# BLOCK 0 :: Data for monotone-cubic-spline.js");
console.log("X" + "\t" + "F");
for (var i = 0; i < N; i += 1) {
    console.log(F[i] + '\t' + X[i]);
}
console.log(" ");
console.log(" ");
console.log("# BLOCK 1 :: Interpolated data for monotone-cubic-spline.js");
console.log("      x       " + "\t\t" + "     P(x)      " + "\t\t" + "    dP(x)/dx     ");
var message = '';
var M = 25;
for (var i = 0; i <= M; i += 1) {
    var x = X[0] + (X[N-1]-X[0])*i/M;
    var rvals = f(x);
    var P = rvals[0];
    var D = rvals[1];
    message += x.toPrecision(15) + '\t' + P.toPrecision(15) + '\t' + D.toPrecision(15) + '\n';
}
console.log(message);

Ссылки

• Фрич, ФН; Карлсон, Р.Э. (1980). «Монотонная кусочно-кубическая интерполяция». SIAM Journal по численному анализу . 17 (2). СИАМ: 238–246. дои : 10.1137/0717021 .
• Догерти, РЛ; Эдельман, А.; Хайман, Дж. М. (апрель 1989 г.). «Кубическая и пятая интерполяция Эрмита, сохраняющая положительность, монотонность или выпуклость» . Математика вычислений . 52 (186): 471–494. дои : 10.2307/2008477 .

Внешние ссылки

• под лицензией GPLv 2 Реализация C++ : MonotCubicInterpolator.cpp MonotCubicInterpolator.hpp