Некоммутативный граф потока сигналов

Система с несколькими входами и несколькими выходами, представленная в виде некоммутативного матричного графа потока сигналов.

В теории автоматов и теории управления , разделах математики , теоретической информатике и системной инженерии некоммутативный граф потока сигналов является инструментом моделирования. взаимосвязанные системы и конечные автоматы путем отображения ребер ориентированного графа в кольцо или полукольцо .

Одиночный вес ребра может представлять собой массив импульсных характеристик сложной системы (см. рисунок справа). или символ алфавита, взятый с входной ленты конечного автомата, в то время как граф может представлять поток информации или переходы состояний.

Какими бы разнообразными ни были эти приложения, в их основе лежит одна и та же основная теория.

Определение

Фрагмент графика потока сигналов.

Рассмотрим n уравнений, включающих n +1 переменную { x ₀ , x ₁ ,..., x _n }.

$x_{i}=\sum _{j=0}^{n}a_{ij}x_{j},\;\;\;1\leq i\leq n,$

с элементами _ij в кольце или полукольце R . Свободная переменная x ₀ соответствует исходной вершине v ₀ , поэтому не имеет определяющего уравнения. Каждому уравнению соответствует фрагмент ориентированного графа G =( V , E ), как показано на рисунке.

ребер определяют функцию f от E до R. Веса Наконец, зафиксируйте выходную вершину v _m . Граф потока сигналов представляет собой совокупность этих данных S = ( G =( V , E ), v ₀ , v _m $\in$ В , ж : Е → р ). Уравнения могут не иметь решения, но когда оно есть,

$x_{m}=Tx_{0},$

с T элементом R, называемым усилением .

Метод обратного цикла

Существует несколько некоммутативные обобщения правила Мейсона . Наиболее распространенным является метод обратной петли (иногда называемый методом прямой обратной петли (FRL) , имеющий двойной метод обратной обратной петли (BRL) ). Первое строгое доказательство приписывается Риглю, поэтому его иногда называют правилом Ригля .

Как и в случае с правилом Мейсона , эти Выражения усиления объединяют термины теоретико-графовым способом (петлевые коэффициенты усиления, произведения путей и т. д.). Известно, что они справедливы над произвольным некоммутативным кольцом и над полукольцом регулярных выражений.

Формальное описание

Метод начинается с перечисления всех путей от входа до выхода, индексируется j $\in$ Дж . Мы используем следующие определения:

• Произведение j -го пути представляет собой (злоупотребляя обозначениями) кортеж из k _j весов ребер вдоль него:

$p_{j}=(w_{k_{j}}^{(j)},\ldots ,w_{2}^{(j)},w_{1}^{(j)}).$

• Разделить v вершину v означает заменить ее источником и стоком с учетом исходной инцидентности и весов (это обратный морфизму графа, переводящий источник и сток в ) .
• Коэффициент усиления петли вершины v относительно подграфа H — это коэффициент усиления от источника к приемнику графа потока сигналов, разделенного в точке v после удаления всех вершин, не входящих в H .
• Каждый путь определяет порядок вершин вдоль него. На пути j коэффициент равен i - го узла FRL (BRL) (1- S _i ^(к) ) ⁻¹ где S _я ^(к) — коэффициент усиления i -й вершины вдоль j -й относительно подграфа, полученного удалением v ₀ и всех вершин перед ним (позади него).

Вклад j -го пути в выигрыш - это произведение по пути, чередующееся между весами произведений пути и узловые коэффициенты:

$T_{j}=\prod _{i=k_{j}}^{1}(1-S_{i}^{(j)})^{-1}w_{i}^{(j)},$

поэтому общий выигрыш равен

$T=\sum _{j\in J}T_{j}.$

Пример

Некоммутативный граф потока сигналов от x до z

Рассмотрим показанный график потока сигналов . От x до z существует два произведения пути: ( d ) и ( e,a ). Вдоль ( d ) вклады FRL и BRL совпадают, поскольку оба имеют одинаковый коэффициент усиления контура (разделение которого снова появляется в правом верхнем углу таблицы ниже):

$f+e(1-b)^{-1}c,$

Умножив коэффициент узла и вес пути, его вклад в усиление составит

$T_{d}=\left[1-f-e(1-b)^{-1}c\right]^{-1}d.$

Вдоль пути ( e,a ) FRL и BRL немного различаются, каждый из которых имеет отдельные разделения вершин y и z, как показано в следующей таблице.

Добавляя к T _d попеременное произведение коэффициентов узлов и весов путей, мы получаем два выражения выигрыша:

$T^{(FRL)}=\left[1-f-e(1-b)^{-1}c\right]^{-1}d+\left[1-f-e(1-b)^{-1}c\right]^{-1}e(1-b)^{-1}a,$

и

$T^{(BRL)}=\left[1-f-e(1-b)^{-1}c\right]^{-1}d+(1-f)^{-1}e\left[1-b-c(1-f)^{e}\right]^{-1}a,$

Эти значения легко увидеть, используя тождества ( ab ) ⁻¹ = б ⁻¹ а ⁻¹ и ) (1 ба - ⁻¹ =(1- аб ) ⁻¹ а .

Приложения

Матричные графики прохождения сигналов

Рассмотрим уравнения

$y_{i}=\sum _{j=1}^{2}a_{ij}x_{j}+\sum _{j=1}^{2}b_{ij}y_{j}$

и

$z_{i}=\sum _{j=1}^{2}c_{ij}y_{j},$

Эту систему можно смоделировать как скалярный граф потока сигналов с несколькими входами и выходами. Но переменные естественным образом распадаются на слои, которые можно собрать в векторы. Икс = ( Икс ₁ , Икс ₂ ) ^т у знак равно ( у ₁ , у ₂ ) ^т и z знак равно ( z ₁ , z ₂ ) ^т .В результате получается гораздо более простой матричный график потока сигналов , как показано на рисунке вверху статьи.

Применение метода прямого обратного цикла тривиально, поскольку существует один продукт пути ( C , A ) с одним коэффициентом усиления цикла B в точке y . Таким образом, в качестве матрицы эта система имеет очень компактное представление своей карты ввода-вывода:

$T=C(1-B)^{-1}A.$

Готово Автоматически

Представление конечного автомата в виде (некоммутативного) графа потока сигналов над полукольцом.

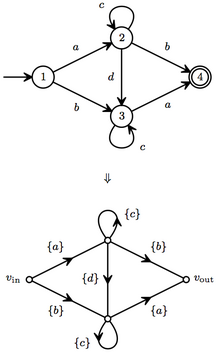
Важным видом некоммутативного графа потока сигналов является конечный автомат над алфавитом. $\Sigma$.

Последовательные соединения соответствуют конкатенации слов, которую можно расширить до подмножеств свободного моноида. $\Sigma ^{*}$. Для А , Б $\subseteq \Sigma ^{*}$

$A\cdot B=\{ab\mid a\in A,b\in B\}.$

Параллельные соединения соответствуют объединению множеств , которое в этом контексте часто пишется A + B .

Наконец, петли естественным образом соответствуют замыканию Клини.

$A^{*}=\{\lambda \}+A+AA+AAA+\cdots ,$

где $\lambda$ это пустое слово . Сходство с бесконечной геометрической прогрессией

$(1-x)^{-1}=1+x+x^{2}+x^{3}\cdots ,$

является более чем поверхностным, поскольку выражения этой формы служат в этом полукольце «инверсией» .

Таким образом, подмножества $\Sigma ^{*}$ Построенное из конечного числа этих трех операций можно отождествить с полукольцом регулярных выражений . Аналогично, конечные графы, ребра которых взвешены подмножествами $\Sigma ^{*}$ можно отождествить с конечными автоматами, хотя обычно эта теория начинается с одноэлементных множеств, как показано на рисунке.

Этот автомат детерминирован, поэтому мы можем однозначно перечислять пути с помощью слов. При использовании метода обратного цикла вклады пути составляют:

• путь ab имеет узловые коэффициенты ( c ^* , $\lambda$), что дает вклад в выигрыш

$ac^{*}b,$

• путь ada имеет коэффициенты узлов ( c ^* , с ^* , $\lambda$), что дает вклад в выигрыш

$ac^{*}dc^{*}a,$

• путь ba имеет узловые коэффициенты ( c ^* , $\lambda$), что дает вклад в выигрыш

$bc^{*}a.$

Таким образом, язык , принимаемый этим автоматом (выигрыш его графа потока сигналов), представляет собой сумму этих членов

$L=ac^{*}b+ac^{*}dc^{*}a+bc^{*}a.$

См. также

• График потока сигналов
• Правило Мейсона
• Завершено автоматически
• Регулярные выражения

Ссылки

• Андалусси, К.; Чал, З.; Сюёр, К. (2006). «Бесконечный ноль линейных моделей графов облигаций, изменяющихся во времени: графические правила». Проектирование систем автоматизированного управления, Международная конференция IEEE по приложениям управления , 2006 г. стр. 2962–2967. doi : 10.1109/CACSD-CCA-ISIC.2006.4777109 .
• Книга, Рональд; Даже Шимон; Грейбах, Шейла; Отт, Джин (1971). «Неоднозначность в графиках и выражениях» (PDF) . Транзакции IEEE на компьютерах . 100 (2). ИИЭР: 149–153. дои : 10.1109/tc.1971.223204 . S2CID   20676251 .
• Бжозовский, Дж. А.; Маккласки, Э.Дж. младший (1963). «Методы графических потоков сигналов для диаграмм состояний последовательных цепей». Транзакции IEEE на электронных компьютерах (2). ИИЭР: 67–76. дои : 10.1109/PGEC.1963.263416 .
• Грейбах, Шейла (1965). «Новая теорема о нормальной форме для грамматик контекстно-свободной фразовой структуры» . Журнал АКМ . 12 (1). АКМ: 42–52. дои : 10.1145/321250.321254 . S2CID   12991430 .
• Куич, Вернер; Саломаа, Арто (1985). Полукольца, автоматы и языки . Спрингер-Верлаг.
• Лоренс, Чарльз С. (1964). Блок-графы: для моделирования и анализа линейных систем . МакГроу-Хилл.
• Плиам, Джон; Ли, Э. Брюс (1995). «О глобальных свойствах взаимосвязанных систем» . Транзакции IEEE в схемах и системах I: Фонд. Теория и приложения . 42 (12). ИИЭР: 1013–1017. дои : 10.1109/81.481196 .
• Ригл, Дэрил; Лин, премьер-министр (1972). «Матричные графики потоков сигналов и оптимальный топологический метод оценки их усиления». Транзакции IEEE по теории цепей . 19 (5). ИИЭР: 427–435. дои : 10.1109/tct.1972.1083542 .