Перемещение груза

Пантограф

Тренироваться

Винтовка

Примеры движущегося груза.

Сила

Осциллятор

Масса

Виды движущегося груза.

В структурной динамике движущаяся нагрузка со временем меняет точку приложения нагрузки. Примеры включают транспортное средство, которое движется по мосту. и поезд, движущийся по рельсам.

Характеристики

В вычислительных моделях нагрузка обычно применяется как

• простая безмассовая сила,
• осциллятор, или
• сила инерции (массовая и безмассовая сила).

Существуют многочисленные исторические обзоры проблемы движущейся нагрузки. Ряд публикаций посвящен аналогичным проблемам.

Фундаментальная монография посвящена безмассовым нагрузкам. Инерционная нагрузка в численных моделях описана в

Неожиданное свойство дифференциальных уравнений, описывающих движение массовой частицы, движущейся по струне, балке Тимошенко и пластине Миндлина , описано в . Это разрыв траектории массы вблизи конца пролета (хорошо видимый в струне на скорости v =0,5 с ). Подвижная нагрузка существенно увеличивает перемещения. Критическая скорость, при которой рост перемещений максимальный, должна учитываться в инженерных проектах.

Конструкции, несущие движущиеся нагрузки, могут иметь конечные размеры или могут быть бесконечными и периодически опираться или располагаться на упругом фундаменте.

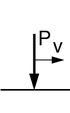
Рассмотрим просто опертую струну длиной l , площадью поперечного сечения A , массовой плотностью ρ, растягивающей силой N , на которую действует постоянная сила P. движется с постоянной скоростью v . Уравнение движения струны под действием движущей силы имеет вид

$-N{\frac {\partial ^{2}w(x,t)}{\partial x^{2}}}+\rho A{\frac {\partial ^{2}w(x,t)}{\partial t^{2}}}=\delta (x-vt)P\ .$

Перемещения любой точки свободно опертой струны задаются синусоидальным рядом.

$w(x,t)={\frac {2P}{\rho Al}}\sum _{j=1}^{\infty }{\frac {1}{\omega _{(j)}^{2}-\omega ^{2}}}\left(\sin(\omega t)-{\frac {\omega }{\omega _{(j)}}}\sin(\omega _{(j)}t)\right)\sin {\frac {j\pi x}{l}}\ ,$

где

$\omega ={\frac {j\pi v}{l}}\ ,$

и естественная круговая частота струны

$\omega _{(j)}^{2}={\frac {j^{2}\pi ^{2}}{l^{2}}}{\frac {N}{\rho A}}\ .$

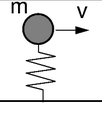
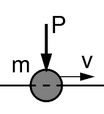
В случае инерционно движущейся нагрузки аналитические решения неизвестны. В уравнение движения добавляется член, связанный с инерцией движущегося груза. Сосредоточенная масса m, сопровождаемая точечной силой P :

$-N{\frac {\partial ^{2}w(x,t)}{\partial x^{2}}}+\rho A{\frac {\partial ^{2}w(x,t)}{\partial t^{2}}}=\delta (x-vt)P-\delta (x-vt)m{\frac {{\mbox{d}}^{2}w(vt,t)}{{\mbox{d}}t^{2}}}\ .$

Сходимость решения для различного числа членов.

Последним членом из-за сложности вычислений инженеры часто пренебрегают. Влияние нагрузки сведено к безмассовой нагрузке. Иногда в точке контакта размещают осциллятор. Такие подходы приемлемы только в низком диапазоне скоростей движущегося груза. В более высоких диапазонах как амплитуда, так и частота колебаний существенно различаются при обоих видах нагрузки.

Дифференциальное уравнение можно решить полуаналитическим способом только для простых задач. Ряд, определяющий решение, хорошо сходится, и на практике достаточно 2-3 членов. Более сложные задачи можно решить методом конечных элементов. или метод конечных элементов пространства-времени .

немассовая нагрузка	инерционная нагрузка
Колебания струны под действием движущейся безмассовой силы ( v =0,1 с ); c – скорость волны. Колебания струны под действием движущейся безмассовой силы ( v =0,5 с ); c – скорость волны.	Колебания струны под действием движущейся силы инерции ( v =0,1 с ); c – скорость волны. Колебания струны под действием движущейся силы инерции ( v =0,5 с ); c – скорость волны.

Прерывистость траектории массы хорошо видна и в пучке Тимошенко. Высокая жесткость на сдвиг подчеркивает это явление.

Колебания балки Тимошенко: красные линии – оси балки во времени, черная линия – траектория массы (w ₀ – статический прогиб).

Подход Ренодо против подхода Якушева

Подход Ренодо

$\delta (x-vt){\frac {\mbox{d}}{{\mbox{d}}t}}\left[m{\frac {{\mbox{d}}w(vt,t)}{{\mbox{d}}t}}\right]=\delta (x-vt)m{\frac {{\mbox{d}}^{2}w(vt,t)}{{\mbox{d}}t^{2}}}\ .$

Yakushev approach

${\frac {\mbox{d}}{{\mbox{d}}t}}\left[\delta (x-vt)m{\frac {{\mbox{d}}w(vt,t)}{{\mbox{d}}t}}\right]=-\delta ^{\prime }(x-vt)mv{\frac {{\mbox{d}}w(vt,t)}{{\mbox{d}}t}}+\delta (x-vt)m{\frac {{\mbox{d}}^{2}w(vt,t)}{{\mbox{d}}t^{2}}}\ .$

Безмассовая струна под действием движущейся инерционной нагрузки

Рассмотрим безмассовую струну, которая является частным случаем задачи о движущейся инерционной нагрузке. Первым, кто решил проблему, был Смит. Анализ будет следовать решению Фрибы. Предполагая ρ =0, уравнение движения струны под движущейся массой можно привести к следующей форме

$-N{\frac {\partial ^{2}w(x,t)}{\partial x^{2}}}=\delta (x-vt)P-\delta (x-vt)\,m{\frac {{\mbox{d}}^{2}w(vt,t)}{{\mbox{d}}t^{2}}}\ .$

Мы налагаем одноопорные граничные условия и нулевые начальные условия. Для решения этого уравнения воспользуемся свойством свертки. Считаем безразмерными перемещения струны y и безразмерное время τ :

Безмассовая струна и движущаяся масса – траектория массы.

$y(\tau )={\frac {w(vt,t)}{w_{st}}}\ ,\ \ \ \ \tau \ =\ {\frac {vt}{l}}\ ,$

где w _st — статический прогиб в середине строка. Решение дается суммой

$y(\tau )={\frac {4\,\alpha }{\alpha \,-\,1}}\,\tau \,(\tau -1)\,\sum _{k=1}^{\infty }\,\prod _{i=1}^{k}{\frac {(a+i-1)(b+i-1)}{c+i-1}}\;{\frac {\tau ^{k}}{k!}}\ ,$

где α – безразмерные параметры:

$\alpha ={\frac {Nl}{2mv2}}\,>\,0\ \ \ \wedge \ \ \ \alpha \,\neq \,1\ .$

Параметры a , b и c приведены ниже.

$a_{1,2}={\frac {3\,\pm \,{\sqrt {1+8\alpha }}}{2}}\ ,\ \ \ \ \ b_{1,2}={\frac {3\,\mp \,{\sqrt {1+8\alpha }}}{2}}\ ,\ \ \ \ \ c=2\ .$

Безмассовая струна и движущаяся масса – траектория массы, α=1.

В случае α =1 рассматриваемая задача имеет замкнутое решение: $y(\tau )=\left[{\frac {4}{3}}\tau (1-\tau )-{\frac {4}{3}}\tau \left(1+2\tau \ln(1-\tau )+2\ln(1-\tau )\right)\right]\ .$