Проблема треугольника Кобона

Проблема треугольника Кобона — нерешенная проблема комбинаторной геометрии, впервые сформулированная Кобоном Фудзимурой (1903–1983). Задача требует наибольшего числа N ( k ) непересекающихся треугольников, стороны которых лежат на наборе из k прямых . Вариации задачи рассматривают проективную плоскость, а не евклидову плоскость, и требуют, чтобы треугольники не пересекались никакими другими линиями расположения. [1]
Известные верхние границы
[ редактировать ]Сабуро Тамура доказал, что количество непересекающихся треугольников, реализуемых формулой линии не более . Г. Клеман и Ж. Бадер убедительнее доказали, что эта граница не может быть достигнута, когда конгруэнтно 0 или 2 (по модулю 6). [2] Таким образом, максимальное количество треугольников в этих случаях не более чем на один меньше. Те же границы можно эквивалентно сформулировать без использования функции пола следующим образом:
Решения, дающие такое количество треугольников, известны, когда это 3, 4, 5, 6, 7, 8, 9, 13, 15 или 17. [3] Для k = 10, 11 и 12 лучшие известные решения достигают количества треугольников на один меньше верхней границы.
Известные конструкции
[ редактировать ]Известны следующие границы:
| к | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | ОЭИС |
| Верхняя граница Тамуры для N ( k ) | 1 | 2 | 5 | 8 | 11 | 16 | 21 | 26 | 33 | 40 | 47 | 56 | 65 | 74 | 85 | 96 | 107 | 120 | 133 | А032765 |
| Верхняя граница Клемана и Бадера | 1 | 2 | 5 | 7 | 11 | 15 | 21 | 26 | 33 | 39 | 47 | 55 | 65 | 74 | 85 | 95 | 107 | 119 | 133 | - |
| самое известное решение | 1 | 2 | 5 | 7 | 11 | 15 | 21 | 25 | 32 | 38 | 47 | 53 | 65 | 72 | 85 | 93 | 104 | 115 | 130 | А006066 |
В проективной плоскости
[ редактировать ]
Версия задачи в проективной плоскости допускает большее количество треугольников. В этом варианте удобно включить линию на бесконечности в число заданных линий, после чего треугольники появляются в трех формах:
- обычные треугольники среди остальных линий, ограниченные тремя конечными отрезками,
- треугольники, ограниченные двумя лучами, встречающимися в общей вершине, и отрезком линии, находящимся на бесконечности, и
- треугольники, ограниченные конечным отрезком прямой и двумя параллельными лучами, пересекающимися в вершине бесконечной прямой.
Например, расположение пяти конечных линий, образующих пентаграмму , вместе с шестой линией, находящейся на бесконечности, имеет десять треугольников: пять в пентаграмме и еще пять, ограниченные парами лучей.
Д. Фордж и Дж. Л. Рамирес Альфонсин предложили метод перехода от расположения в проективной плоскости с линии и треугольники (максимально возможный для ), с некоторыми дополнительными свойствами, к другому решению с линии и треугольники (опять же максимум), с теми же дополнительными свойствами. По их наблюдениям, этот метод можно начать с описанного выше проективного расположения шести линий и десяти треугольников, создавая оптимальные проективные расположения, число линий которых равно
Таким образом, в проективном случае существует бесконечно много различных чисел прямых, для которых известно оптимальное решение. [1]
Примеры
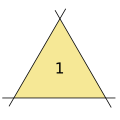
[ редактировать ]- 3 линии, 1 треугольник
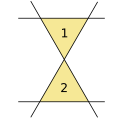
- 4 линии, 2 треугольника
- 5 линий, 5 треугольников
- 6 линий, 7 треугольников
- 7 линий, 11 треугольников
См. также
[ редактировать ]- Теорема Робертса о треугольнике о минимальном количестве треугольников, которые линии могут образовывать
Ссылки
[ редактировать ]- ^ Перейти обратно: а б Фордж, Д.; Рамирес Альфонсин, Х.Л. (1998), «Расположение прямых в реальной проективной плоскости», Дискретная и вычислительная геометрия , 20 (2): 155–161, doi : 10.1007/PL00009373 .
- ^ «Г. Клеман и Дж. Бадер. Более точная верхняя граница для числа треугольников Кобон. Черновая версия, 2007 г.» (PDF) . Архивировано из оригинала (PDF) 11 ноября 2017 г. Проверено 3 марта 2008 г.
- ^ Эд Пегг-младший о математических играх
Внешние ссылки
[ редактировать ]- Йоханнес Бадер, «Треугольники Кобон»