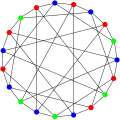
Граф Робертсона

Граф Робертсона
Граф Робертсона является гамильтоновым.
Назван в честь	Нил Робертсон
Вершины	19
Края	38
Радиус	3
Диаметр	3
Обхват	5
Автоморфизмы	24 ( Д 12 )
Хроматическое число	3
Хроматический индекс	5
Толщина книги	3
Номер очереди	2
Характеристики	Клетка гамильтониан
Таблица графиков и параметров

В математической области теории графов граф Робертсона или (4,5)-клетка — это 4- правильный неориентированный граф с 19 вершинами и 38 ребрами, названный в честь Нила Робертсона .

Граф Робертсона — это уникальный граф (4,5)-клеток , открытый Робертсоном в 1964 году. В качестве клеточного графа это наименьший 4-регулярный граф с обхватом 5.

Он имеет хроматическое число 3, хроматический индекс 5, диаметр 3, радиус 3 и является как 4- вершинно-связным , так и 4- реберно-связным . Имеет толщину книги 3 и номер очереди 2.

Граф Робертсона также является гамильтоновым графом , который имеет 5376 различных направленных гамильтоновых циклов.

Граф Робертсона — один из самых маленьких графов с номером COP 4.

Алгебраические свойства

Граф Робертсона не является вершинно-транзитивным графом , и его полная группа автоморфизмов изоморфна группе диэдра порядка 24, группе симметрий правильного двенадцатиугольника , включая как вращения, так и отражения.

Характеристический полином графа Робертсона равен

$(x-4)(x-1)^{2}(x^{2}-3)^{2}(x^{2}+x-5)$

$(x^{2}+x-4)^{2}(x^{2}+x-3)^{2}(x^{2}+x-1).\$

Галерея

• 
  График Робертсона, нарисованный в оригинальной публикации.
• 
  Хроматическое число графа Робертсона равно 3.
• 
  Хроматический индекс графа Робертсона равен 5.